常见的排序算法——冒泡排序（二）

本文记述了针对冒泡排序微小改动的基本思想和一份参考实现代码，并在说明了算法的性能后用随机数据进行了验证。

◆ 思想

更少的比较可以节省一定的时间，此改动可以减少更小范围的比较。

（把水平陈列的数组逆时针旋转90°后，有助于理解后续的内容。）

将包含顶层以下的所有元素作为待排序范围，将该范围以上的所有元素作为已排序范围。通过一一比较相邻的两个元素，自底向上地将待排序范围内的最大元素放到顶层。然后将包含次顶层以下的所有元素作为待排序范围，重复以上的比较和交换，直至待排序范围中只剩一个元素为止。处理当前待排序范围后，如果没有发生元素交换，则说明数组已经排好序，无需再缩小比较范围做进一步的比较。如要得到逆序的结果，则仅需改变比较的方向即可。

◆ 实现

排序代码采用《算法（第4版）》的“排序算法类模板”实现。(代码中涉及的基础类，如 Array，请参考算法文章中涉及的若干基础类的主要API）

// bubble2.hxx

...

class Bubble2
{

    ...

    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    void
    sort(Array<_T> & a)
    {
        int N = a.size();
        bool xd = true;         // #1
        for (int i = N-1; i > 0 && xd; --i) {           // #2
            xd = false;
            for (int j = 0; j < i; ++j)             // #3
                if (__less__(a[j+1], a[j])) {
                    __exch__(a, j+1, j);
                    xd = true;              // #4
                }
        }
    }
    
    ...
    
    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    bool
    __less__(_T const& v, _T const& w)
    {
        return v.compare_to(w) < 0;         // #5
    }

    ...
    
    template
    <
        class _T,
        class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type
    >
    static
    void
    __exch__(Array<_T> & a, int i, int j)
    {
        _T t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    ...

设置一个判断是否有交换的标志位（#1）。反复处理待排序范围，直至没有发生元素交换或待排序范围中只剩一个元素（#2）。取消标志位，通过一一比较相邻的两个元素，自底向上地将待排序范围内的最大元素放到顶层（#3）。如果发生交换，设置标志位（#4）。将 '<' 改为 '>'，即得到逆序的结果（#5）。

◆ 性能

时间复杂度	空间复杂度	是否稳定
N^2	1	是

◆ 验证

测试代码采用《算法（第4版）》的倍率实验方案，用随机数据验证其正确性并获取时间复杂度数据。

// test.cpp
    
...

time_trial(int N)
{
    Array<Double> a(N);
    for (int i = 0; i < N; ++i) a[i] = Std_Random::random();    // #1
    Stopwatch timer;
    Bubble2::sort(a);                     // #2
    double time = timer.elapsed_time();
    assert(Bubble2::is_sorted(a));            // #3
    return time;
}

...

test(char * argv[])
{
    int T = std::stoi(argv[1]);          // #4
    double prev = time_trial(512);
    Std_Out::printf("%10s%10s%7s\n", "N", "Time", "Ratio");
    for (int i = 0, N = 1024; i < T; ++i, N += N) {            // #5
        double time = time_trial(N);
        Std_Out::printf("%10d%10.3f%7.1f\n", N, time, time/prev);   // #6
        prev = time;
    }
}

...

用 [0,1) 之间的实数初始化待排序数组（#1），打开计时器后执行排序（#2），确保得到正确的排序结果（#3）。整个测试过程要执行 T 次排序（#4）。每次执行排序的数据规模都会翻倍（#5），并以上一次排序的时间为基础计算倍率（#6），

此测试在实验环境一中完成，

$ g++ -std=c++11 test.cpp std_out.cpp std_random.cpp stopwatch.cpp type_wrappers.cpp

$ ./a.out 8

     N      Time  Ratio
  1024     0.300    4.1
  2048     1.198    4.0
  4096     4.777    4.0
  8192    19.069    4.0
 16384    76.458    4.0
 32768   305.503    4.0
 65536  1213.778    4.0
131072  4877.336    4.0

可以看出，随着数据规模的成倍增长，排序所花费的时间将是上一次规模的 4 倍。将数据反映到以 2 为底数的对数坐标系中，可以得到如下图像，

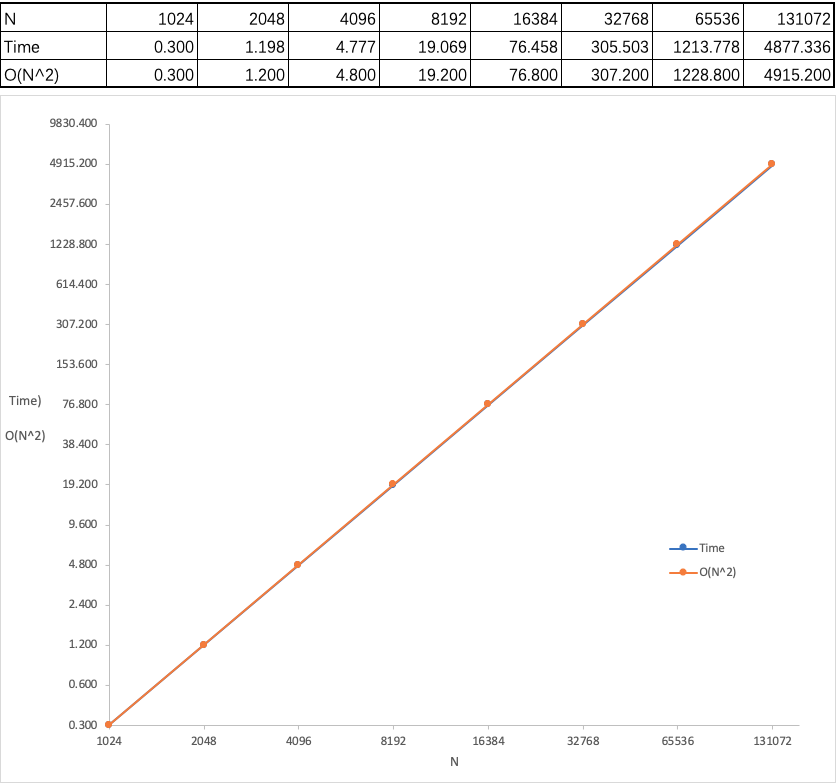
O(N^2) 代表了平方级别复杂度下的理论排序时间，该行中的数据是以 Time 行的第一个数据为基数逐一乘 4 后得到的结果（因为做的是倍率实验，所以乘 (2)^2 即 4）。

与冒泡排序的测试数据相比，并没有达到减少时间的目的。可以得出结论，针对随机数据而言，减少更小范围的比较并不能减少排序时间。

◆ 最后

完整的代码请参考 [gitee] cnblogs/18131389 。

查看性能对比，了解此算法与其它排序算法的相似性和差异性。

写作过程中，笔者参考了《算法（第4版）》一书中的“排序算法类模板”和倍率实验。致作者 Sedgwick，Wayne 及译者谢路云。