四则运算生成命令行程序 (Python)
Github项目地址:Github Pages
结对项目成员:张鹏 3118004985 郑靓 3118004988
一、项目需求分析

二、功能实现

三、代码实现or功能说明
★ GUI功能扩展说明 🎈

- 采用了多线程的界面,任何操作不会阻塞其他操作,例如:可以在生成答案的同时批改作业
- 得益于上面的设计,可以同时生成多个表达式文件,存储形式如下所示

- 对于错误的输入,会有提示,如下所示
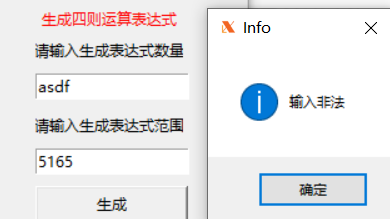
- 对于文件选择后,点击批改,对于文件的格式有错误检查
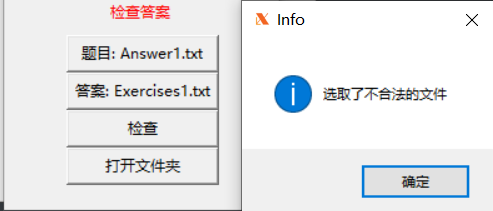
通过后缀表达式的计算过程,确保生成表达式满足题目所有要求,避免重复的表达式生成 (详参下文 '判断重复的思路' )
★ 多线程(防止I/O阻塞)🎈
- 创建生产者线程, 传参进队列 'queue'
producer = multiprocessing.Process(target=self.expression_generator, args=(queue,))
- 创建消费者进程, 传参进队列 'queue'
consumer = multiprocessing.Process(target=self.io_operation, args=(queue,))
- 生产者——循环生成表达式 及其答案
- 构建随机表达式 以及生成其答案 ' Arithmetic(self.domain).create_arithmetic() '
- 生成其表达式对应答案 ' Calculate(expression).cal_expression() '
- 将生成后缀表达式过程中每次的结果 以及操作符集合 保存到 字典 (' self.no_repeat_dict ' ) 中, 从而确保生成等式不相同 (即 3+2+1 与 1+2+3 不相等, 6×8 与 8×6 相等)
- 生成完成后, 把表达式 以及 答案添加到队列 queue 中
- 消费者——循环生成表达式 及其答案
- 通过死循环不断获取队列内容, 若队列传出 'None' 信号, 消费者进程停止
- 解析从队列获取的内容, 并将多次获取的表达式以及答案保存到 缓冲区(Buffer) 中, 有限次数后开始写入文件 并 销毁缓冲区内容
★ 判断重复的思路 🎈
- 由于考虑到题目说1+2+3,2+1+3相等,1+2+3和3+2+1是不相等的,我一开始是从字符串的处理考虑,但是复杂度有点高。
- 所以换了一个角度考虑,从运算顺序入手,就想到用后缀表达式进行去重,并且这样也不用考虑括号,符合题目所说的(1+2)+3和1+2+3相等
- 具体就是存储每一次运算出来的结果,然后进行一一比较
例如(这里举的是比较简单的例子): 1+2+3,压入的数字:[3, 6]; 3+2+1,压入的数字:[5,6],所有两个判断为不相等 - 但是这样会出现1+3和2+2判断为重复的情况,所以添加两个数组——[操作数],[运算符],作为比较的依据
- 再来考虑效率,用字典的数据结构,以答案为键,其他三个比较标志作为值,只在答案相等的情况下判重
附:最终选定了添加后缀计算的去重模式,就是为了避免 (1÷1)+3 和 1+(3÷1) 这种不为重复表达式的情况,但是效率确实比只判断(操作数、运算符)的模式低了
——创建数据结构
# 用答案作为索引构建的字典,
{
"1'2/2": [
[[压入的数字], [操作数], [运算符]],
[[压入的数字], [操作数], [运算符]],
...
]
}
# 通过比较上述字典, 确认新表达式是否已经在上述字典中
def judge_repeat(self, answer, test_sign):
for expression_sign in self.no_repeat_dict[answer]:
# 记录相同的个数
same_num = 0
for i in range(3):
if collections.Counter(expression_sign[i]) == collections.Counter(test_sign[i]):
same_num += 1
# 如果中间结果、操作数、运算符均相等,则为重复
if same_num == 3:
return False
return True
★ 生成表达式思路 🎈
# 表达式列表形式
['10', '÷', '(', '8/9', '÷', '51', ')']
- 随机生成操作数列表,运算符列表
- 根据以上两个列表构建无括号表达式
- 根据运算符个数,随机生成括号个数,最大个数为( 1->0, 2->1, 3->2 )
- 再随机括号位置,维护操作数位置列表,插入括号
# 生成表达式
def create_arithmetic(self):
# 生成随机操作数、运算符列表
self.create_operand_list()
self.create_operator_list()
i = 0
# 构建表达式列表
self.expression_split.append(self.operand_list[i])
self.expression_split.append(self.operator_list[i])
i += 1
while i < len(self.operator_list):
self.expression_split.append(self.operand_list[i])
self.expression_split.append(self.operator_list[i])
i += 1
self.expression_split.append(self.operand_list[i])
# 插入括号
if self.operator_num != 1:
bracket_num = random.randint(1, self.operator_num - 1)
self.insert_bracket(bracket_num)
# 删除无用括号
self.del_useless_bracket()
return [self.expression_split, self.operand_list, self.operator_list]
★ 计算思路(后缀表达式) 🎈
生成后缀表达式
- 设置两个栈,一个用以存储运算符,一个用以存储后缀表达式
- 循环遍历表达式列表,如果是操作数,则加入后缀栈
- 否则如果是运算符则进入以下判断
- 如果运算符栈为空,或者栈顶为 ( ,则压入运算符栈
- 否则如果当前运算符大于栈顶运算符的优先级,则压入运算符栈
- 否则弹栈并压入后缀栈直到优先级大于栈顶或空栈
- 否则如果遇到括号则进入以下判断
- 若为 ( 直接压入运算符栈
- 否则弹栈并压入后缀栈直到遇到 (
- 将运算符栈剩余的元素压入后缀栈
计算后缀表达式
- 用一个栈(calculate_stack)作为计算中介
- 循环遍历后缀表达式,若为数字压入 calculate_stack
- 否则从 calculate_stack 弹出两个数字,分别化为分数类,进行计算,结果压入 calculate_stack
- 重复 2-3,若期间运算结果出现负数,或除数为0,则返回false
- 直至后缀表达式遍历完成,返回 calculate_stack 的栈顶
代码 🎈
class Calculate(object):
def __init__(self, expression):
self.expression = expression
# 分数加法 a1/b1 + a2/b2 = (a1b2 + a2b1)/b1b2
@staticmethod
def fraction_add(fra1, fra2):
molecular = fra1.molecular * fra2.denominator + fra2.molecular * fra1.denominator
denominator = fra1.denominator * fra2.denominator
return Fraction(molecular, denominator)
# 分数减法 a1/b1 - a2/b2 = (a1b2 - a2b1)/b1b2
@staticmethod
def fraction_minus(fra1, fra2):
molecular = fra1.molecular * fra2.denominator - fra2.molecular * fra1.denominator
denominator = fra1.denominator * fra2.denominator
return Fraction(molecular, denominator)
# 分数乘法 a1/b1 * a2/b2 = a1a2/b1b2
@staticmethod
def fraction_multiply(fra1, fra2):
molecular = fra1.molecular * fra2.molecular
denominator = fra1.denominator * fra2.denominator
return Fraction(molecular, denominator)
# 分数除法 a1/b1 ÷ a2/b2 = a1b2/a2b1
@staticmethod
def fraction_divide(fra1, fra2):
molecular = fra1.molecular * fra2.denominator
denominator = fra1.denominator * fra2.molecular
return Fraction(molecular, denominator)
# 基本运算选择器
def operate(self, num1, num2, operater):
if not isinstance(num1, Fraction):
num1 = Fraction(num1)
if not isinstance(num2, Fraction):
num2 = Fraction(num2)
# 计算结果
if operater == '+':
return self.fraction_add(num1, num2)
if operater == '-':
return self.fraction_minus(num1, num2)
if operater == '×':
return self.fraction_multiply(num1, num2)
if operater == '÷':
return self.fraction_divide(num1, num2)
# 转成逆波兰
def generate_postfix_expression(self):
# 运算符栈
operator_stack = []
# 后缀栈
postfix_stack = []
for element in self.expression:
# 如果是操作数则添加
if element not in operators:
postfix_stack.append(element)
# 如果是运算符则按优先级
elif element in operator.values():
# 运算符栈为空,或者栈顶为(,则压栈
if not operator_stack or operator_stack[-1] == '(':
operator_stack.append(element)
# 若当前运算符优先级大于运算符栈顶,则压栈
elif priority[element] >= priority[operator_stack[-1]]:
operator_stack.append(element)
# 否则弹栈并压入后缀队列直到优先级大于栈顶或空栈
else:
while operator_stack and priority[element] < priority[operator_stack[-1]]:
postfix_stack.append(operator_stack.pop())
operator_stack.append(element)
# 如果遇到括号
else:
# 若为左括号直接压入运算符栈
if element == '(':
operator_stack.append(element)
# 否则弹栈并压入后缀队列直到遇到左括号
else:
while operator_stack[-1] != '(':
postfix_stack.append(operator_stack.pop())
operator_stack.pop()
while operator_stack:
postfix_stack.append(operator_stack.pop())
return postfix_stack
# 计算表达式(运算过程出现负数,或者除数为0,返回False,否则返回Fraction类)
def cal_expression(self):
# 生成后缀表达式
expressions_result = self.generate_postfix_expression()
# 存储阶段性结果
stage_results = []
# 使用list作为栈来计算
calculate_stack = []
# 后缀遍历
for element in expressions_result:
# 若是数字则入栈, 操作符则将栈顶两个元素出栈
if element not in operators:
calculate_stack.append(element)
else:
# 操作数
num1 = calculate_stack.pop()
# 操作数
num2 = calculate_stack.pop()
# 除数不能为0
if num1 == "0" and element == '÷':
return [False, []]
# 结果
result = self.operate(num2, num1, element)
if result.denominator == 0 or '-' in result.to_string():
return [False, []]
stage_results.append(result.to_string())
# 结果入栈
calculate_stack.append(result)
# 返回结果
return [calculate_stack[0], stage_results]
四、实际测试
通过命令行控制
python ArithmeticCLMode.py [args|args]
[args]
├─ -h --help # 输出帮助信息
├─ -n # 指定生成表达式数量,默认100
├─ -r # 指定生成表达式各个数字的取值范围,默认100
├─ -a # 需和-e参数共同使用进行批改,指定答案文件
├─ -e # 需和-a参数共同使用进行批改,指定练习文件
└─ -g # 开启GUI
通过gui控制
python ArithmeticGMode.py
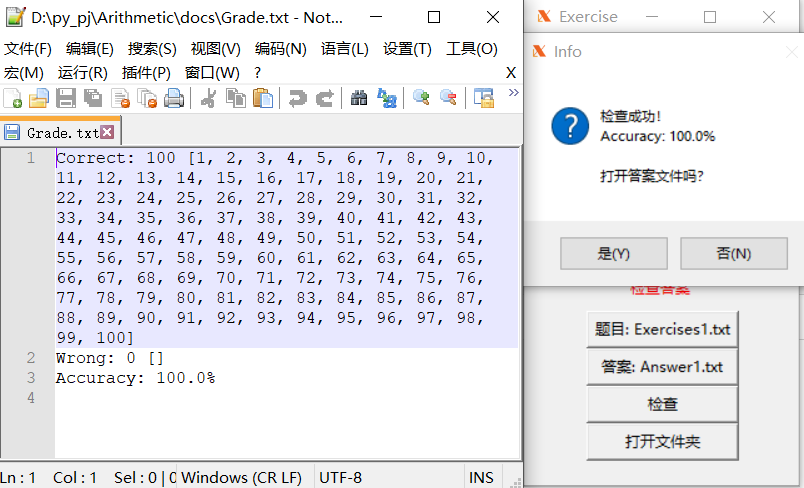
执行代码
python ArithmeticCLMode.py -n 100 -r 100

# 将上述执行生成的 Exercise.txt 中的1~10题的答案改为错误 执行
python ArithmeticCLMode.py -e ./docs/Exercise.txt -a ./docs/Answer.txt

五、效能分析
由Pycharm测试输出性能测试

程序耗时在多线程中的 生成表达式及计算, 以及I/O操作
在值域1000的情况下各生成不同数量级四则运算的耗时测试
六、PSP表格 🚩
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 30 | 10 |
| Development | 开发 | 1055 | 1480 + 120 |
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 335 |
| · Design Spec | · 生成设计文档 | 60 | 35 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 5 | 5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 5 |
| · Design | · 具体设计 | 200 | 120 |
| · Coding | · 具体编码 | 600 | 580 +120 |
| · Code Review | · 代码复审 | 30 | 120 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 150 |
| Reporting | 报告 | 85 | 130 |
| · Test Report | · 测试报告 | 60 | 30 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 15 | 90 |
| 合计 | 1170 | 1620 + 120 |
七、总结 🚀
优点:
- 在此次项目合作中,我们通过 "Notion" 这一个软件完成设计我们的 开发流程、工作分配以及我们的代码规范的设计。我们将需求列出,根据难度不同从而安排开发流程,每个人根据自己能力特出点不同而去做不同的需求,再通过交流约定我们每个人的接口。简化开发流程。
- 交流和配合都挺顺畅的
不足:
- 开发中各个模块的依赖关系在开发任务中没有处理清楚,导致双方都有空窗期
互评 ❤💛💙
To 郑靓
能力强,效率高,非常积极主动。能根据自己日常使用的工具提高效率,在实际开发中有明确的开发流程思路,开发过程中有部分函数代码注释思路不清。
To 张鹏
配合和交流能力强,效率高,能主动揽接任务,思维挺好的,但比较被动




