力扣剑指OFFER
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
限制:
2 <= n <= 100000
来源:力扣
class Solution {
public int findRepeatNumber(int[] nums) {
return exchange(nums);
}
// set 简单直接
// 数据多的时候可能会慢
private int useSet(int[] nums){
Set<Integer> rec = new HashSet<>();
for(int n : nums){
if(!rec.add(n)){
return n;
}
}
return -1;
}
// 桶排序 数据稀疏时浪费空间 数据密集速度快
private int useBucketSort(int[] nums){
int space = nums.length;
int[] record = new int[space];
for(int n: nums){
record[n] += 1;
if(record[n] > 1){
return n;
}
}
return -1;
}
//空间O(1),原地排序
private int sort(int[] nums){
Arrays.sort(nums);
int idx = 0;
while(idx < nums.length-1){
if(nums[idx] == nums[idx+1]){
return nums[idx];
}
idx++;
}
return -1;
}
//空间O(1) 交换排序
private int exchange(int[] nums){
//因为 长度为n的数组里的数字大小在0~n-1之间,所以不会有越界
//遍历每个位置,把该位置上的数字放到下标值也等于这个数的位置上去
int i = 0;
//这里是while 循环
while(i < nums.length){
int tmp = nums[nums[i]];
if(tmp == nums[i] && i != nums[i]){
return tmp;
}
nums[nums[i]] = nums[i];
nums[i] = tmp;
if( i == nums[i]) i++;
}
return -1;
}
}
二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
限制:
0 <= n <= 1000
0 <= m <= 1000
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
return findFromLeftDownCorner(matrix, target);
}
//右上角开始找,左边比当前值小,下边比当前值大
public boolean findFromRightUpCorner(int[][] matrix, int target){
int row = matrix.length;
if(row == 0){
return false;
}
int col = matrix[0].length;
if(col == 0){
return false;
}
int i = 0, j = col - 1;
while(i < row && j >= 0){
if(matrix[i][j] == target){
return true;
}else if(matrix[i][j] < target){
i++;
}else if(matrix[i][j] > target){
j--;
}
}
return false;
}
//也可以左下角开始找,右边的比当前值大,上面的比当前值小
public boolean findFromLeftDownCorner(int[][] matrix, int target){
int row = matrix.length;
if(row == 0){
return false;
}
int col = matrix[0].length;
if(col == 0){
return false;
}
int i = row-1, j = 0;
while(i >= 0 && j < col){
if(matrix[i][j] == target){
return true;
}else if(matrix[i][j] < target){
j++;
}else if(matrix[i][j] > target){
i--;
}
}
return false;
}
}
替换空格
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
示例 1:
输入:s = "We are happy."
输出:"We%20are%20happy."
限制:
0 <= s 的长度 <= 10000
class Solution {
// 没什么太大意义: 由于每次替换从 1 个字符变成 3 个字符,使用字符数组可方便地进行替换。建立字符数组地长度为 s 的长度的 3 倍,这样可保证字符数组可以容纳所有替换后的字符。
public String replaceSpace(String s) {
String res = "";
for(int i = 0; i<s.length(); i++)
res += s.charAt(i) == ' '? "%20": s.charAt(i);
return res;
}
}
重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
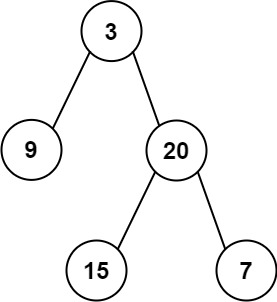
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
限制:
0 <= 节点个数 <= 5000
来源:力扣
对于任意一颗树而言,前序遍历的形式总是
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int[] pre;
int[] in;
int len;
Map<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
pre = preorder;
in = inorder;
len = pre.length;
if(len == 0) return null;
for(int i = 0; i < len; i++) map.put(inorder[i], i);
return build(0, len-1, 0 ,len-1);
}
private TreeNode build(int preL, int preR, int inL, int inR){
if(preL > preR){
return null;
}
int rootVal = pre[preL];
TreeNode root = new TreeNode(rootVal);
int mid = map.get(rootVal);
int size = mid - inL;
root.left = build(preL + 1, preL + size, inL, mid -1);
root.right = build(preL + size + 1, preR, mid + 1, inR);
return root;
}
}
矩阵中的路径
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
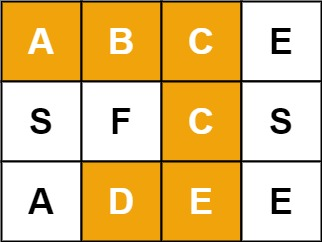
例如,在下面的 3×4 的矩阵中包含单词 "ABCCED"(单词中的字母已标出)。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
提示:
1 <= board.length <= 200
1 <= board[i].length <= 200
board 和 word 仅由大小写英文字母组成
class Solution {
char[][] b;
String w;
int row;
int col;
int[][] directs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public boolean exist(char[][] board, String word) {
b=board;
w=word;
row = board.length;
col = board[0].length;
boolean[][] marks = new boolean[row][col];
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(searchInBoard(marks, 0, i, j)) return true;
}
}
return false;
}
private boolean searchInBoard(boolean[][] marks, int idx, int x, int y){
if(x<0 || x > row - 1 || y < 0 || y > col - 1 || marks[x][y]){
return false;
}
if(b[x][y] != w.charAt(idx)){
return false;
}
if(idx == w.length()-1){
return true;
}
marks[x][y] = true;
boolean res = false;
for(int[] d: directs){
if(searchInBoard(marks, idx+1, x + d[0], y+d[1])){
res = true;
break;
}
}
marks[x][y] = false;
return res;
}
}
机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 100
0 <= k <= 20

class Solution {
boolean[][] marks;
public int movingCount(int m, int n, int k) {
marks = new boolean[m][n];
// return broadSearch(m, n, k);
return deepSearch(m, n, 0, 0, k);
}
// 宽度优先搜索
// 可以只往下和往右搜
private int broadSearch(int m, int n, int k){
Queue<int[]> seeds = new LinkedList<>();
int[][] directs = new int[][]{{1, 0}, {0, 1}};
int cnt = 0;
cnt++;
marks[0][0] = true;
seeds.add(new int[]{0,0});
while(!seeds.isEmpty()){
int[] seed = seeds.remove();
for(int[] direct: directs){
int x = seed[0] + direct[0];
int y = seed[1] + direct[1];
if(x > m -1 || y > n - 1 || marks[x][y] || calSum(x, y) > k){
continue;
}
cnt++;
marks[x][y] = true;
seeds.add(new int[]{x, y});
}
}
return cnt;
}
/**
递归参数:
终止条件: 当 ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过 时,返回 0 ,代表不计入可达解。
递推工作:
标记当前单元格 :将索引 (i, j) 存入 Set visited 中,代表此单元格已被访问过。
搜索下一单元格: 计算当前元素的 下、右 两个方向元素的数位和,并开启下层递归 。
回溯返回值: 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数,代表从本单元格递归搜索的可达解总数。
*/
private int deepSearch(int m, int n, int x, int y, int k){
if(x > m -1 || y > n -1 || marks[x][y] || calSum(x, y) > k){
return 0;
}
marks[x][y] = true;
int cnt = 1;
cnt += deepSearch(m, n, x + 1, y, k);
cnt += deepSearch(m, n, x, y + 1, k);
// 不能回溯,因为路径上的每个点都是一次记录,用过就不能再用了
// marks[x][y] = false;
return cnt;
}
private int calSum(int x, int y){
int sum = 0;
while(x > 0){
sum += x % 10;
x/=10;
}
while(y > 0){
sum += y % 10;
y/=10;
}
return sum;
}
}
I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]k[1]...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
来源:LeetCode
class Solution {
public int cuttingRope(int n) {
return dp(n);
}
/**
dp[i] 表示将长度为 i 的绳子剪成至少两段绳子之后,这些绳子长度的最大乘积
确定状态转移方程
当 i ≥ 2 时,假设对长度为 i 绳子剪出的第一段绳子长度是 j(1≤j<i),则有以下两种方案:
将 i 剪成 j 和 i-j 长度的绳子,且 i−j 不再继续剪,此时的乘积是 j×(i−j) ;
将 i 剪成 j 和 i−j 长度的绳子,且 i−j 继续剪成多段长度的绳子,此时的乘积是 j×dp[i−j] 。
因此,当 j 固定时,有 dp[i]=max(j×(i−j),j×dp[i−j])。由于 j 的取值范围是 1 到 i ,需要遍历所有的 j 得到dp[i]的
*/
public int dp(int n){
int[] dp = new int[n+1];
dp[0] = 0;
dp[1] = 0;
dp[2] = 1;
for(int i = 3; i <= n; i++){
for(int j = 1; j <i - 1; j ++){
dp[i] = Math.max(dp[i], Math.max(j * (i-j),dp[i-j] * j));
}
}
return dp[n];
}
//贪心
//尽量多的3,剩余的用2补全
public int greed(int n){
if(n == 2) return 1;
if(n == 3) return 2;
int threeRemains = n % 3;
int twos = 0;
int threes = 0;
if(threeRemains == 1){
twos = 2;
n -= 3;
}else if(threeRemains == 2){
twos = 1;
}
threes = n / 3;
return (int)Math.pow(3, threes) * (int)Math.pow(2, twos);
}
}
剪绳子 II
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]k[1]...*k[m - 1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 1000
大数求余有以下两个主要公式
公式1:(x+y)%p=(x%p+y%p)%p
证明:
令x=a*p+b,y=c*p+d
有(x+y)%p=[(a+c)*p+b+d]%p
因为(a+c)*p是p的倍数,故略去,而b=x%p,d=y%p
所以,(x+y)%p=(b+d)%p=(x%p+y%p)%p
公式2:(x*y)%p=[(x%p)(y%p)]%p
证明
令x=a*p+b,y=c*p+d
有(x*y)%p=(a*c*p*p+a*d*p+b*c*p+b*d)%p
因为a*c*p*p+a*d*p+b*c*p是p的倍数,故略去,而b=x%p,d=y%p
所以,(x*y)%p=(b*d)%p=[(x%p)*(y%p)]%p
根据上述可推导出:pow(n,m)%p=[(n%p)*pow(n,m-1)%p]%p
class Solution {
int mod = 1000000007;
public int cuttingRope(int n) {
return math(n);
}
// 算法主体与 https://leetcode.cn/problems/jian-sheng-zi-lcof/ 类似,
// 区别在于需要使用快速幂算法求幂次 外加 大数取余
private int math(int b){
if(b < 3) return 1;
if(b == 3) return 2;
if(b % 3 == 0) return (int)(quickPowAndMod(3, b/3) % mod);
if(b % 3 == 1) return (int)((quickPowAndMod(3, b/3-1) * 4) % mod);
if(b % 3 == 2) return (int)((quickPowAndMod(3, b/3) * 2) % mod);
return 0;
}
//快速幂取余
//与快速幂算法类似,每一步多一个取余的步骤,快速幂算法参考
//https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/
private long quickPowAndMod(long b, int n){
long res = 1;
while(n > 0){
if((n & 1) == 1){
res = (res * b) % mod;
}
b = (b * b) % mod;
n = n >> 1;
}
return (int)(res % mod);
}
}
数值的整数次方
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104
来源:LeetCode
class Solution {
public double myPow(double x, int n) {
return n > 0 ? quickMulRecur(x, n) : 1 / quickMulRecur(x, -(long)n);
// return n > 0 ? quickMulIter(x, n) : 1 / quickMulIter(x, -(long)n);
}
//递归版本
private double quickMulRecur(double x, long n){
if(n == 0){
return 1;
}else{
double y = quickMulRecur(x, n / 2);
return n % 2 == 0 ? y * y : y * y * x;
}
}
//迭代版本
//x^9 ==> x^1 * x^8, 9 = (1001b)
private double quickMulIter(double x, long n){
double res = 1;
while (n > 0){
//先用res乘再往前计算x
if((n & 1) == 1){
res *= x;
}
x *= x;
n = n >> 1;
}
return res;
}
}
树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:
0 <= 节点个数 <= 10000
来源:LeetCode
树的很多递归题,想清楚如何分解为子问题就好做了。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
if(B == null) return false;
return inOrderSearch(A, B);
}
private boolean inOrderSearch(TreeNode A, TreeNode B){
if(A == null || B == null) return false;
if(isTwoSub(A, B)) return true;
return inOrderSearch(A.left, B) || inOrderSearch(A.right, B);
}
private boolean isTwoSub(TreeNode a, TreeNode b){
if(b == null) return true;
if(a == null) return false;
if(a.val != b.val) return false;
return isTwoSub(a.left, b.left) && isTwoSub(a.right, b.right);
}
}
表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。
数值(按顺序)可以分成以下几个部分:
若干空格
一个 小数 或者 整数
(可选)一个 'e' 或 'E' ,后面跟着一个 整数
若干空格
小数(按顺序)可以分成以下几个部分:
(可选)一个符号字符('+' 或 '-')
下述格式之一:
至少一位数字,后面跟着一个点 '.'
至少一位数字,后面跟着一个点 '.' ,后面再跟着至少一位数字
一个点 '.' ,后面跟着至少一位数字
整数(按顺序)可以分成以下几个部分:
(可选)一个符号字符('+' 或 '-')
至少一位数字
部分数值列举如下:
["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]
部分非数值列举如下:
["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]
示例 1:
输入:s = "0"
输出:true
示例 2:
输入:s = "e"
输出:false
示例 3:
输入:s = "."
输出:false
示例 4:
输入:s = " .1 "
输出:true
提示:
1 <= s.length <= 20
s 仅含英文字母(大写和小写),数字(0-9),加号 '+' ,减号 '-' ,空格 ' ' 或者点 '.' 。
来源:LeetCode
状态机
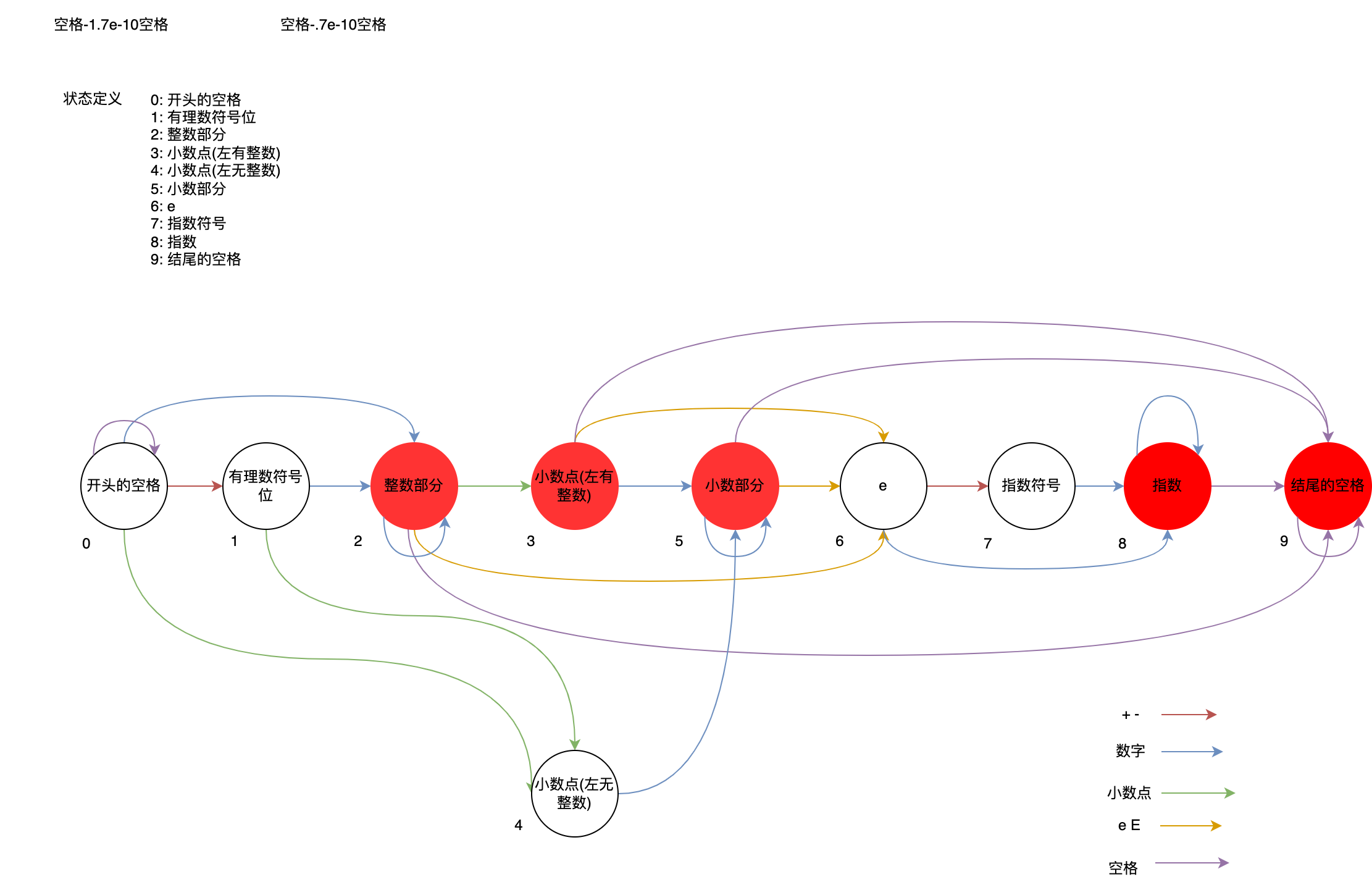
class Solution {
// ' '-空格;'d'-数字; '.'-小数点; 'e'- e; 's'-正负号
private static final Map<Character, Integer>[] statusMap =
new Map[] {
new HashMap<Character, Integer>() {{
put(' ', 0);
put('s', 1);
put('d', 2);
put('.', 4);
}}, //0
new HashMap<Character, Integer>() {{
put('.', 4);
put('d', 2);
}}, //1
new HashMap<Character, Integer>() {{
put('d', 2);
put('e', 6);
put(' ', 9);
put('.', 3);
}}, //2
new HashMap<Character, Integer>() {{
put('d', 5);
put('e', 6);
put(' ', 9);
}}, //3
new HashMap<Character, Integer>() {{
put('d', 5);
}}, //4
new HashMap<Character, Integer>() {{
put('d', 5);
put('e', 6);
put(' ', 9);
}}, //5
new HashMap<Character, Integer>() {{
put('s', 7);
put('d', 8);
}}, //6
new HashMap<Character, Integer>() {{
put('d', 8);
}}, //7
new HashMap<Character, Integer>() {{
put('d', 8);
put(' ', 9);
}}, //8
new HashMap<Character, Integer>() {{
put(' ', 9);
}}, //9
};
private static final Set<Integer> validStatus = new HashSet<Integer>() {{
add(2);
add(3);
add(5);
add(8);
add(9);
}};
public boolean isNumber(String s) {
int status = 0;
for (char c : s.toCharArray()) {
c = getSign(c);
Map<Character, Integer> currentStatusMap = statusMap[status];
if (!currentStatusMap.containsKey(c)) {
return false;
}
status = currentStatusMap.get(c);
}
//2,3,5,8,9是有效终态
return validStatus.contains(status);
}
private char getSign(char c) {
if (c >= '0' && c <= '9') {
return 'd';
}
if (c == '-' || c == '+') {
return 's';
}
if (c == 'e' || c == 'E') {
return 'e';
}
if (c == '.' || c == ' ') {
return c;
}
return '?';
}
}
二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
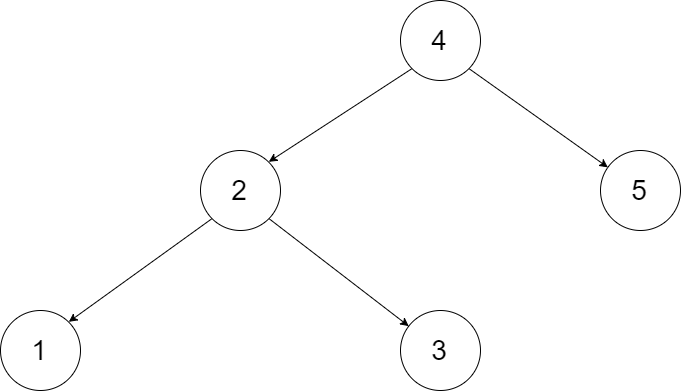
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
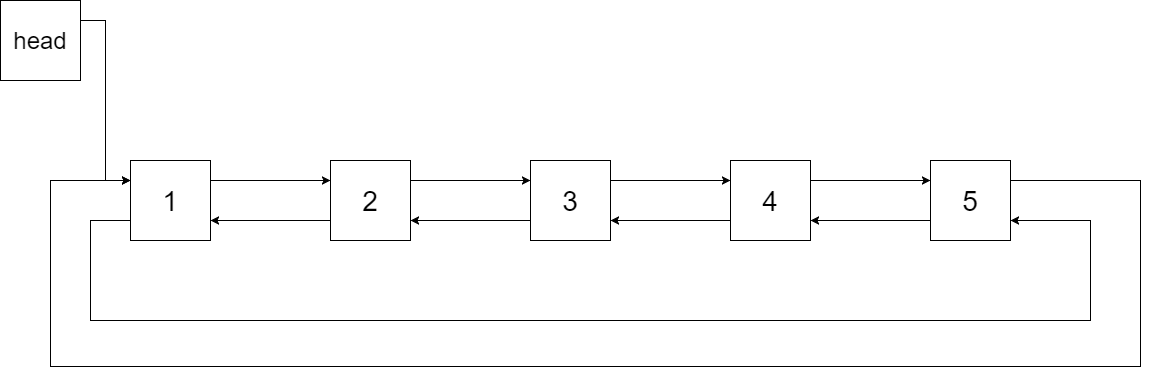
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
//用全局变量保存head pre
private Node pre, head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
inOrderSearch(root);
//最后要把收尾连起来
head.left = pre;
pre.right = head;
return head;
}
//中序遍历能保证按从小到达顺序遍历每个节点。
//我们把之前中序遍历打印节点的操作替换为连接前后节点的操作即可简单完成双向链表的连接
private void inOrderSearch(Node cur){
if(cur == null) return;
inOrderSearch(cur.left);
if(pre==null) head = cur;
else pre.right = cur;
cur.left = pre;
pre = cur;
inOrderSearch(cur.right);
}
}
栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
提示:
0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed是popped的排列。
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
return leftRightSwagger(pushed, popped);
}
//2022/06/20 这个解法过不去第 97/151个用例,但我觉得没问题
private boolean leftRightSwagger(int[] pushed, int[] popped){
int len = pushed.length;
if(len == 0) return true;
int right = findIdx(popped[0], pushed);
if(right == -1) return false;
int left = right;
for(int i = 1; i < len; i++){
if(right+1 < len && pushed[right+1] == popped[i]) right+=1;
else if(left-1 >= 0 && pushed[left-1] == popped[i]) left-=1;
else return false;
}
return true;
}
private int findIdx(int val, int[] arr){
for(int i = 0; i<arr.length; i++){
if(arr[i] == val) return i;
}
return -1;
}
}
damn it
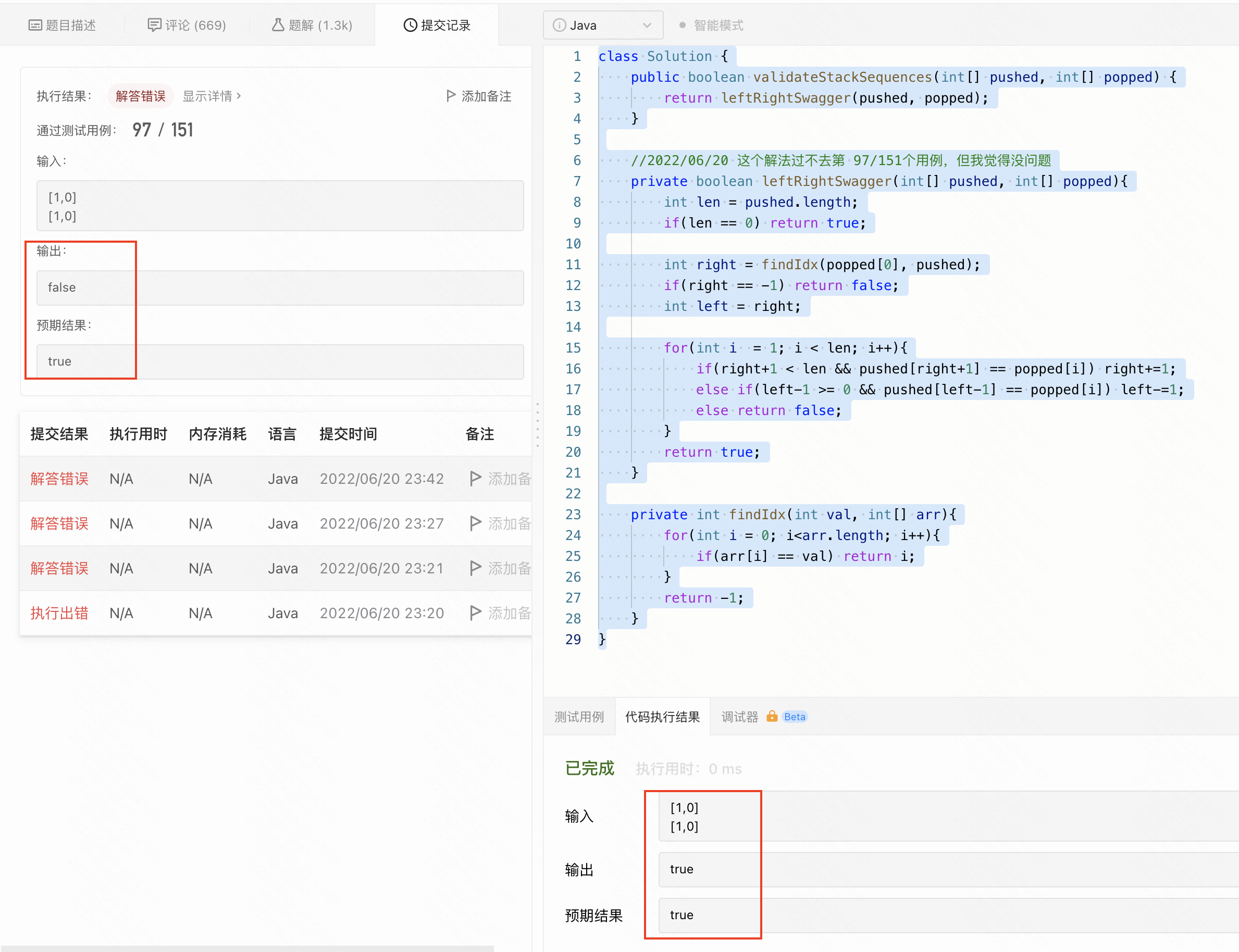
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
return stackMock(pushed, popped);
}
/**
考虑借用一个辅助栈 stackstack ,模拟 压入 / 弹出操作的排列。根据是否模拟成功,即可得到结果。
入栈操作: 按照压栈序列的顺序执行。
出栈操作: 每次入栈后,循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立,将符合弹出序列顺序的栈顶元素全部弹出。
*/
private boolean stackMock(int[] pushed, int[] popped){
if(pushed.length <= 0 ) return true;
Stack<Integer> stack = new Stack<>();
int p = 0;
for(int i: pushed){
stack.push(i);
while(!stack.isEmpty() && stack.peek() == popped[p]){
stack.pop();
p++;
}
}
return stack.isEmpty();
}
//2022/06/20 这个解法过不去第 97/151个用例,但我觉得没问题
private boolean leftRightSwagger(int[] pushed, int[] popped){
int len = pushed.length;
if(len == 0) return true;
int right = findIdx(popped[0], pushed);
if(right == -1) return false;
int left = right;
for(int i = 1; i < len; i++){
if(right+1 < len && pushed[right+1] == popped[i]) right+=1;
else if(left-1 >= 0 && pushed[left-1] == popped[i]) left-=1;
else return false;
}
return true;
}
private int findIdx(int val, int[] arr){
for(int i = 0; i<arr.length; i++){
if(arr[i] == val) return i;
}
return -1;
}
}
字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = "abc"
输出:["abc","acb","bac","bca","cab","cba"]
限制:
1 <= s的长度<= 8
class Solution {
private String tmp;
private List<String> result = new ArrayList<>();
public String[] permutation(String s) {
tmp = s;
bt(new ArrayList<>(), new boolean[tmp.length()]);
result = result.stream().distinct().collect(Collectors.toList());
int len = result.size();
String[] res = new String[len];
for(int i = 0; i< len; i++){
res[i] = result.get(i);
}
return res;
}
private void bt(List<Character> cur, boolean[] mark){
if(cur.size() == tmp.length()) result.add(stringListToString(cur));
for(int i = 0; i < tmp.length(); i++){
if(mark[i]) continue;
mark[i] = true;
cur.add(tmp.charAt(i));
bt(cur, mark);
mark[i] = false;
cur.remove(cur.size()-1);
}
}
private String stringListToString(List<Character> cur){
String res = "";
for(char c: cur)
res += c;
return res;
}
}
I. 从上到下打印二叉树
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回:
[3,9,20,15,7]
提示:
节点总数 <= 1000
无脑宽搜
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int[] levelOrder(TreeNode root) {
Deque<TreeNode> queue = new ArrayDeque<>();
if (root == null)
return new int[0];
queue.offer(root);
List<Integer> res = new ArrayList<>();
while(!queue.isEmpty()){
TreeNode node = queue.pop();
res.add(node.val);
if(node.left!=null) queue.offer(node.left);
if(node.right!=null) queue.offer(node.right);
}
int[] result = new int[res.size()];
for(int i = 0; i<res.size(); i++)
result[i] = res.get(i);
return result;
}
}
复杂链表的复制
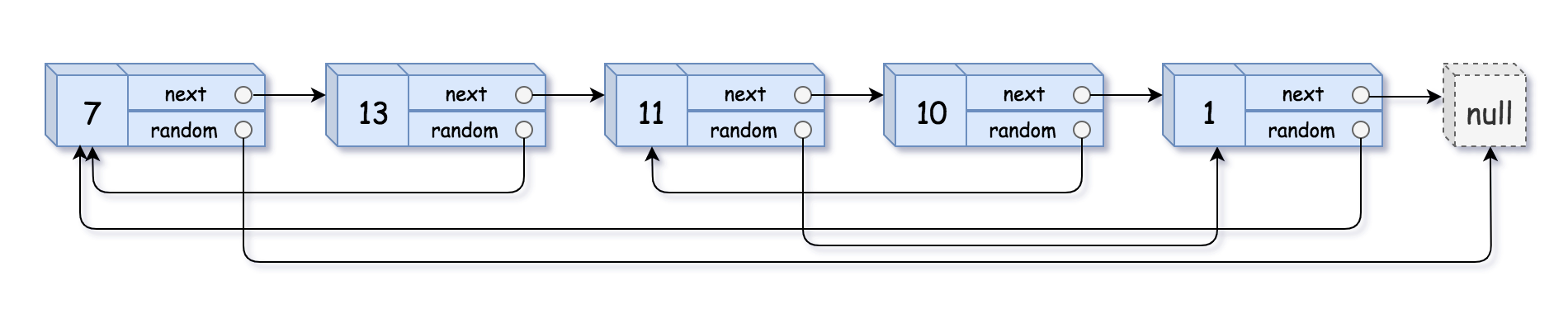
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
示例 1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3
输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
示例 4:
输入:head = []
输出:[]
解释:给定的链表为空(空指针),因此返回 null。
提示:
-10000 <= Node.val <= 10000
Node.random为空(null)或指向链表中的节点。
节点数目不超过1000。
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
public Node copyRandomList(Node head) {
// return copyWithMap(head);
return copyWithSonNode(head);
}
// 使用map保存
private Node copyWithMap(Node head){
if (head == null) return null;
Map<Node,Node> map = new HashMap<>();
Node cur = head;
while(cur != null){
map.put(cur, new Node(cur.val));
cur = cur.next;
}
cur = head;
while(cur != null){
map.get(cur).next = map.get(cur.next);
map.get(cur).random = map.get(cur.random);
cur = cur.next;
}
return map.get(head);
}
//复制子节点并拆分
private Node copyWithSonNode(Node head){
if (head == null) return null;
Node cur = head;
//复制子节点
while(cur != null){
Node tmp = cur.next;
Node newCur = new Node(cur.val);
newCur.next = tmp;
cur.next = newCur;
cur = tmp;
}
cur = head;
//复制random 指针
while(cur != null){
if(cur.random != null){
cur.next.random = cur.random.next;
}
cur = cur.next.next;
}
//拆分链表
cur = head;
Node newHead = cur.next;
Node newCur = newHead;
while(newCur.next != null){
cur.next = cur.next.next;
newCur.next = newCur.next.next;
cur = cur.next;
newCur = newCur.next;
}
cur.next = null; //
return newHead;
}
}
礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
0 < grid.length <= 200
0 < grid[0].length <= 200
class Solution {
public int maxValue(int[][] grid) {
int row = grid.length;
int col = grid[0].length;
for(int i = 1; i< row; i++){
grid[i][0] = grid[i-1][0] + grid[i][0];
}
for(int j = 1; j < col; j++){
grid[0][j] = grid[0][j-1] + grid[0][j];
}
for(int i = 1; i < row; i++){
for(int j = 1; j < col; j++){
grid[i][j] = Math.max(grid[i-1][j], grid[i][j-1]) + grid[i][j];
}
}
return grid[row-1][col-1];
}
}
III. 从上到下打印二叉树 III
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:
给定二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[20,9],
[15,7]
]
提示:
节点总数 <= 1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
return levelDeque(root);
}
public List<List<Integer>> levelDeque(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
Deque<TreeNode> queue = new ArrayDeque<>();
if (root == null)
return ans;
queue.offer(root);
boolean isFromLeft = false;
while(!queue.isEmpty()){
Deque<Integer> temp = new ArrayDeque<>();
int size = queue.size(); //记一下每层的节点数,用这个来判断一层是否遍历完了
for(int i = 0; i<size; i++){
TreeNode node = queue.poll();
if(isFromLeft){
temp.offerFirst(node.val);
}else{
temp.offerLast(node.val);
}
if(node.left!=null) queue.offer(node.left);
if(node.right!=null) queue.offer(node.right);
}
isFromLeft = !isFromLeft;
//不得不说有时候java真是大笨蛋语言,java程序员基本上不会对list按下标取值和赋值
ans.add(new LinkedList<Integer>(temp));
}
return ans;
}
}
c++就很nice,
// 二叉树层次遍历 (按 偶数层顺序、奇数层逆序 的顺序,将每层结点打印到数组中)
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
if(root == NULL) return result;
queue<TreeNode*> que;
que.push(root);
int level = 0;
while(!que.empty()) {
int len = que.size();//这里先存储了每一层数组的大小
result.push_back(vector<int>(len));//首先根据每层数组大小进行拓展
for(int i = 0; i < len; ++i) {
TreeNode* cur = que.front();
que.pop();
if(level % 2 == 0) {//根据奇偶层进行从前到后或者从后向前的赋值
result[level][i] = cur->val;
} else {
result[level][len-i-1] = cur->val;
}
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
++level;
}
return result;
}
};
二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
class Solution {
public boolean verifyPostorder(int[] postorder) {
return recurse(postorder, 0, postorder.length-1);
}
private boolean recurse(int[] arr, int i, int j){
if(i>=j) return true;
int p = i;
while(arr[p] < arr[j]) p++;
int m = p;
while(arr[p] > arr[j]) p++;
return p == j && recurse(arr, i, m-1) && recurse(arr, m, j-1);
}
}
剑指 Offer 34. 二叉树中和为某一值的路径
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1
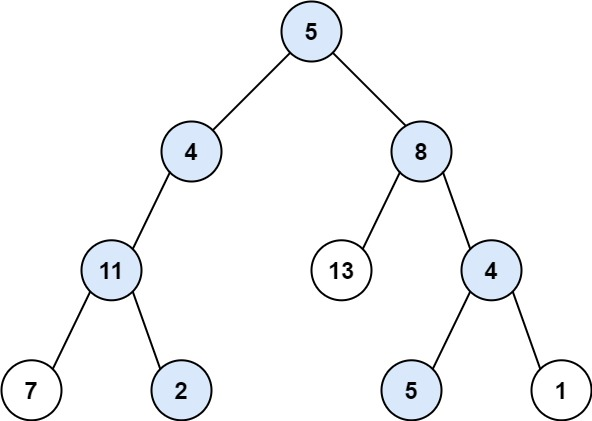
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int target) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Deque<Integer> tmp = new LinkedList<>();
dfs(root, res, tmp, target);
return res;
}
private void dfs(TreeNode root, List<List<Integer>> res, Deque<Integer> tmp, int target) {
target -= root.val;
tmp.offerLast(root.val);
if (target == 0 && root.left == null && root.right == null) {
res.add(new ArrayList<>(tmp));
}
if (root.left != null) {
dfs(root.left, res, tmp, target);
}
if (root.right != null) {
dfs(root.right, res, tmp, target);
}
tmp.pollLast();
}
}
剑指 Offer 56 - I. 数组中数字出现的次数
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
示例 1:
输入:nums = [4,1,4,6]
输出:[1,6]或[6,1]
示例 2:
输入:nums = [1,2,10,4,1,4,3,3]
输出:[2,10]或[10,2]
限制:
2 <= nums.length <= 10000
力扣
思路:
假设两个不同的数分别为A 和B。
- 将所有的数相异或得到的结果为C,两两相同的数将会抵消,则 C = A^B。又因为A != B, 因此 C != 0;
- 找到C的二进制表示中的任意不为0的一位,设为第idx位,则数字A和B在第idx是不同的。用这位给数组中的所有数字分组: 将idx位为0的分为一组 group0,为1的分为一组group2。则我们可以得到如下保证:
- 相同的数字必定会被分到同一组, 因为如果两个数字相同, 则他们在任意一位都是相同的, 因此在idx位也是相同的, 因此必定分到同一组;
- 由上面的第2点可知数字A和B必定分到不同的组。
- 经过上面第2步, 得到group0和group1分别是包含多对两两相同数字外加一个不同数字的数组。将他们分别异或,则可以找出两组中出现一次的数字。
class Solution {
public int[] singleNumbers(int[] nums) {
int ox = 0;
for(int i : nums) ox = (ox ^ i);
int idx = 0;
while((ox & 1) != 1){
ox = ox >> 1;
idx++;
}
int x = 0, y = 0;
for(int i: nums){
if(((i >> idx) & 1) == 0){
x = (x ^ i);
}else{
y = (y ^ i);
}
}
return new int[]{x, y};
}
}
剑指 Offer 56 - II. 数组中数字出现的次数 II
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
示例 1:
输入:nums = [3,4,3,3]
输出:4
示例 2:
输入:nums = [9,1,7,9,7,9,7]
输出:1<\br>
限制:
1 <= nums.length <= 10000
1 <= nums[i] < 2^31
[力扣]https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-ii-lcof)
思路:
int数组中其他的数字都出现3次,只有一个数字出现一次。如果我们将数组中的每个数都按位相加,研究第idx位,则idx位的值X是所有数字第idx的值加起来。因为除一个数字外其他数字都出现三次,则X对3取模就是唯一出现的那个数字的值。
把按位相加的结果的每位都对3取模,就得到了出现一次的那个数字的每个数位的表示,将其从二进制还原为十进制即可。
class Solution {
public int singleNumber(int[] nums) {
int[] bits = new int[32];
for(int i: nums){
for(int j = 0; j < 32; j++){
if(((i >> j)&1) == 1) bits[j]++;
}
}
int res = 0;
for(int i = 0; i < 32; i++){
bits[i] = bits[i] % 3;
if(bits[i] == 1) res += (1 <<i );
}
return res;
}
}
剑指 Offer 46. 把数字翻译成字符串
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
示例 1:
输入:12258
输出:5
解释:12258有5种不同的翻译,分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"
提示:
0 <= num < 231
LeetCode

class Solution {
public int translateNum(int num) {
String numStr = String.valueOf(num);
int a = 1, b = 1;
for(int i = 2; i <= numStr.length(); i++){
int tmp = (numStr.substring(i-2, i).compareTo("10")>=0 && numStr.substring(i-2, i).compareTo("25")<=0)? a + b:a;
b = a;
a = tmp;
}
return a;
}
}
剑指 Offer 48. 最长不含重复字符的子字符串
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 1:
输入:"abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入:"bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
解法一refer: refer
class Solution {
public int lengthOfLongestSubstring(String s) {
return solve2(s);
}
public int solve2(String s){
Map<Character, Integer> dups = new HashMap<>();
int j=-1, res = 0;
for(int i = 0; i < s.length(); i++){
char tmp = s.charAt(i);
if(dups.containsKey(tmp))
j = Math.max(j,dups.get(tmp));
dups.put(tmp, i);
res = Math.max(res, i-j);
}
return res;
}
// 维护不重复的窗口 windows, 另用一个set辅助快速判断是否有重复
public int solve1(String s) {
Set<Character> dups = new HashSet<>();
List<Character> windows = new ArrayList<>();
int res = 0;
for(int i = 0; i < s.length(); i++){
char tmp = s.charAt(i);
//不重复就一直往set和 窗口里加
if(dups.add(tmp)){
windows.add(tmp);
}else{
//有重复就计算下最大长度, 然后将窗口的左边界一直往右推,一直推到重复元素推出窗口为止
res = Math.max(res, dups.size());
int j = windows.indexOf(tmp);
for(int k = 0; k <= j; k++){
dups.remove(windows.get(0));
windows.remove(0);
}
windows.add(tmp);
dups.add(tmp);
}
}
res = Math.max(res, dups.size());
return res;
}
}
剑指 Offer 49. 丑数
我们把只包含质因子
2、3和5的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
示例:
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
1 是丑数。
n 不超过1690。
LeetCode
设dp[i]是第i个丑数, 且dp[i]一定是dp[a] 乘以2 , 或者dp[b]乘以3, 或者dp[c]乘以5转移而来的,且dp[a]、dp[b], dp[c]都是丑数序列里在i之前的某个丑数。
我们分别维护好上次用来乘以2、乘以3、乘以5的到当前丑数的最近的下标p2, p3, p5。需要求当前的p[i]的时候,我们尝试用p2, p3, p5 上的数乘以2, 3, 5来的到下一个dp[i]的备选, 其中最小的那个就是当前的dp[i], 然后看是p2, p3, p5中的哪个转移而来的dp[i], 就将谁的下标往前推进。
class Solution {
public int nthUglyNumber(int n) {
int[] dp = new int[n];
dp[0] = 1;
int p2 = 0, p3 = 0, p5 = 0;
for(int i = 1; i < n; i++){
dp[i] = Math.min(dp[p2] * 2, Math.min(dp[p3] *3, dp[p5] *5));
if(dp[i] == dp[p2] * 2) p2++;
if(dp[i] == dp[p3] * 3) p3++;
if(dp[i] == dp[p5] * 5) p5++;
}
return dp[n-1];
}
}
剑指 Offer 59 - II. 队列的最大值
请定义一个队列并实现函数
max_value得到队列里的最大值,要求函数max_value、push_back和pop_front的均摊时间复杂度都是O(1)。
若队列为空,pop_front和max_value需要返回 -1
示例 1:
输入:
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出:[null,null,null,2,1,2]
示例 2:
输入:
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出:[null,-1,-1]]
限制:
1 <= push_back,pop_front,max_value的总操作数 <= 10000
1 <= value <= 10^5
为了解决上述问题,我们只需记住当前最大值出队后,队列里的下一个最大值即可。
具体方法是使用一个双端队列 deque,在每次入队时,如果 deque 队尾元素小于即将入队的元素 value,则将小于 value 的元素全部出队后,再将 value 入队;否则直接入队。
class MaxQueue {
private Queue<Integer> queue;
private Deque<Integer> maxQueue;
public MaxQueue() {
queue = new LinkedList<>();
maxQueue = new LinkedList<>();
}
public int max_value() {
return maxQueue.isEmpty()? -1 : maxQueue.peekFirst();
}
public void push_back(int value) {
while(!maxQueue.isEmpty() && maxQueue.peekLast() < value) maxQueue.pollLast();
queue.offer(value);
maxQueue.offerLast(value);
}
public int pop_front() {
if(queue.isEmpty()){
return -1;
}
int res = queue.poll();
if(res == maxQueue.peekFirst()) maxQueue.pollFirst();
return res;
}
}
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue obj = new MaxQueue();
* int param_1 = obj.max_value();
* obj.push_back(value);
* int param_3 = obj.pop_front();
*/
剑指 Offer 66. 构建乘积数组
给定一个数组
A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B[i]的值是数组A中除了下标i以外的元素的积, 即B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
示例:
输入:[1,2,3,4,5]
输出:[120,60,40,30,24]
提示:
所有元素乘积之和不会溢出 32 位整数
a.length <= 100000
力扣
仿照前缀和的方式,用前缀积的方式来简化计算。遍历两遍数组:
- 从前往后遍历,计算前缀积数组b, 其中
b[i]=a[0]*a[1]*...*a[i-1] - 从后往前遍历, 计算后缀积数组d, 其中
d[i]=a[len-1] * a[len-2] * ... * a[i+1]
要求的结果B[i]=b[i]*d[i]
进一步的, 我们并不需要保存后缀积数组,后缀积用一次就可以往前推进一次
class Solution {
public int[] constructArr(int[] a) {
if(a == null || a.length == 0) return new int[0];
int[] res = new int[a.length];
res[0] = 1;
for(int i = 1; i < a.length; i++) res[i] = res[i-1] * a[i-1];
int tmp = 1;
for(int i = a.length-2; i >= 0; i--){
tmp *= a[i+1];
res[i] *= tmp;
}
return res;
}
}
剑指 Offer 60. n个骰子的点数
把
n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这n个骰子所能掷出的点数集合中第i小的那个的概率。
示例 1:
输入: 1
输出:[0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
输入: 2
输出:[0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
限制:
1 <= n <= 11
LeetCode
题解refer
设f(n, x)表示使用n个骰子掷出来加和为x的概率,现在我们在这个基础上考虑增加一个骰子。则新增的骰子掷出1,2,3,4,5,6的概率各为1/6,把点数加到x上,可以得到在f(n, x)的前提下,新增一个骰子后,f(n+1, x+1), f(n+1, x+2), f(n+1, x+3), f(n+1, x+4), f(n+1, x+5), f(n+1, x+6)的概率也各为1/6。根据条件概率公式f(a) = f(b) * f(a|b)可知
f(n+1, x+1) = f(n, x) / 6, f(n+1, x+2) = f(n, x) / 6, f(n+1, x+3) = f(n, x) / 6, f(n+1, x+4) = f(n, x) / 6,f(n+1, x+5) = f(n, x) / 6, f(n+1, x+6) = f(n, x) / 6 -- 从n到n+1的递推公式
对于一个骰子的情况,我们知道f(1,1) = 1/6, f(1,2) = 1/6, f(1,3) = 1/6, f(1,4) = 1/6,f(1,5) = 1/6, f(1,6) = 1/6。 -- 初始条件
结合递推公式和初始条件,我们可以算出n为任意值的最终结果。
class Solution {
public double[] dicesProbability(int n) {
double[] arr = new double[6];
Arrays.fill(arr, 1.0/6.0);
for(int i = 2; i <=n; i++){
double[] tmp = new double[5*i+1];
for(int j = 0; j < arr.length; j++){
for(int k = 1; k <=6; k++){
tmp[j+k-1] += arr[j]/6;
}
}
arr = tmp;
}
return arr;
}
}
剑指 Offer 67. 把字符串转换成整数
写一个函数 StrToInt,实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围,请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
示例 1:
输入: "42"
输出: 42
示例 2:
输入: " -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3:
输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ,因为它的下一个字符不为数字。
示例 4:
输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。
因此无法执行有效的转换。
示例 5:
输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。
LeetCode
class Solution {
public int strToInt(String str) {
if(Objects.equals(str, "") || str == null) return 0;
int i = 0;
while (i < str.length() && str.charAt(i) == ' ') {
i++;
if (i >= str.length()) {
return 0;
}
}
char firstChar = str.charAt(i);
if ((firstChar > '9' || firstChar < '0') && (firstChar != '+' && firstChar != '-')) {
return 0;
}
int flag = firstChar == '-' ? -1 : 1;
long res = 0;
if (firstChar >= '1' && firstChar <= '9') {
res += firstChar - 48;
}
i++;
while (i < str.length()) {
if (str.charAt(i) >= '0' && str.charAt(i) <= '9') {
res = res * 10 + str.charAt(i) - 48;
if ((flag * res > Integer.MAX_VALUE) || (flag * res < Integer.MIN_VALUE)) {
return flag < 0 ? Integer.MIN_VALUE : Integer.MAX_VALUE;
}
} else {
break;
}
i++;
}
res *= flag;
if (res > Integer.MAX_VALUE) {
return Integer.MAX_VALUE;
}
if (res < Integer.MIN_VALUE) {
return Integer.MIN_VALUE;
}
return (int) res;
}
}
剑指 Offer 63. 股票的最大利润
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
限制:
0 <= 数组长度 <= 10^5
动态规划解析:
状态定义: 设动态规划列表dp,dp[i]代表以prices[i]为结尾的子数组的最大利润(以下简称为 前i日的最大利润 )。
转移方程: 由于题目限定 “买卖该股票一次” ,因此前i日最大利润dp[i]等于前i−1日最大利润dp[i-1]和第i日卖出的最大利润中的最大值。
前i日最大利润 =max(前 (i-1) 日最大利润, 第 i 日价格 - 前 i 日最低价格)
dp[i] = max(dp[i - 1], prices[i] - min(prices[0:i]))
初始状态:dp[0] = 0,即首日利润为0;
返回值:dp[n−1],其中n为dp列表长度。
链接
class Solution {
public int maxProfit(int[] prices) {
int min = Integer.MAX_VALUE, maxProfit = 0;
for(int price : prices){
min = Math.min(min, price);
maxProfit = Math.max(maxProfit, price-min);
}
return maxProfit;
}
}
剑指 Offer 64. 求1+2+…+n
求
1+2+...+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
示例 1:
输入: n = 3
输出: 6
示例 2:
输入: n = 9
输出: 45
限制:
1 <= n <= 10000
LeetCode
用递归取代循环,用短路取代条件判断
class Solution {
public int sumNums(int n) {
boolean flag = n > 0 && (n += sumNums(n-1)) > 0;
return n;
}
}
剑指 Offer 27. 二叉树的镜像
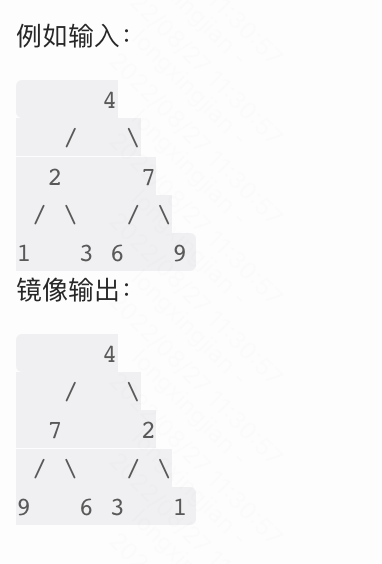
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
限制:
0 <= 节点个数 <= 1000
LeetCode
解法1: 递归
// 递归是从下往上的顺序交换子节点的位置
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return root;
if(root.left != null) mirrorTree(root.left);
if(root.right != null) mirrorTree(root.right);
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
return root;
}
}
解法2: 栈/队列辅助
// 辅助队列/栈 是自上而下的交换子节点的位置
private TreeNode withQueue(TreeNode root){
if(root == null) return root;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode node = queue.poll();
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
TreeNode tmp = node.left;
node.left = node.right;
node.right = tmp;
}
return root;
}
剑指 Offer 28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root =[1,2,2,null,3,null,3]
输出:false
限制:
0 <= 节点个数 <= 1000
(LeetCode)(https://leetcode.cn/problems/dui-cheng-de-er-cha-shu-lcof)
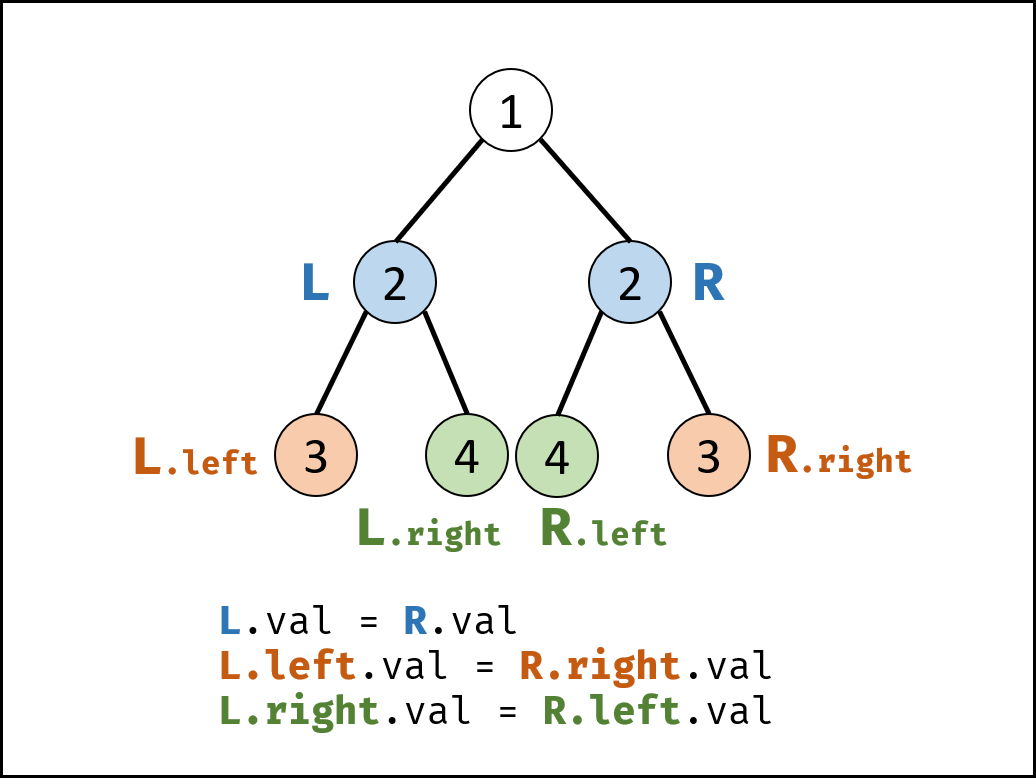
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return isSymmetric(root.left, root.right);
}
private boolean isSymmetric(TreeNode left, TreeNode right){
if(left == null) return right == null;
if(right == null) return left == null;
if(left.val != right.val) return false;
return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
}
}
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数在数组的前半部分,所有偶数在数组的后半部分。
示例:
输入:nums = [1,2,3,4]
输出:[1,3,2,4]
注:[3,1,2,4]也是正确的答案之一。
提示:
0 <= nums.length <= 50000
0 <= nums[i] <= 10000
class Solution {
private int[] numsInternel;
public int[] exchange(int[] nums) {
return useFrontBackPointer(nums);
}
//双指针一个从前往后一个从后往前
public int[] useFrontBackPointer(int[] nums){
int lf = 0, rh = nums.length-1;
while(lf < rh){
if(nums[lf] % 2 == 1){
lf++;
}
if(nums[rh] % 2 == 0){
rh--;
}
if(lf < rh){
int tmp = nums[lf];
nums[lf] = nums[rh];
nums[rh] = tmp;
}
}
return nums;
}
//双指针都从前往后
public int[] exchangeTwoPointer(int[] nums) {
numsInternel = nums;
int oddIdx = findNext(-1, 1);
int evenIdx = findNext(-1, 0);
while(evenIdx >= 0 && oddIdx >= 0){
if(oddIdx < evenIdx){
oddIdx = findNext(oddIdx, 1);
}else{
swap(oddIdx, evenIdx);
oddIdx = findNext(oddIdx, 1);
evenIdx = findNext(evenIdx, 0);
}
}
return numsInternel;
}
private int findNext(int idx, int mod){
while(++idx < numsInternel.length){
if(numsInternel[idx] % 2 == mod) return idx;
}
return -1;
}
private void swap(int lt, int rh){
int tmp = numsInternel[lt];
numsInternel[lt] = numsInternel[rh];
numsInternel[rh] = tmp;
}
}
剑指 Offer 15. 二进制中1的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为 汉明重量).)。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用 二进制补码 记法来表示有符号整数。因此,在上面的 示例 3 中,输入表示有符号整数 -3。
示例 1:
输入:n = 11 (控制台输入 00000000000000000000000000001011)
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:n = 128 (控制台输入 00000000000000000000000010000000)
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:n = 4294967293 (控制台输入 11111111111111111111111111111101,部分语言中 n = -3)
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
输入必须是长度为 32 的 二进制串 。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
return hammingWeight2(n);
}
public int hammingWeight1(int n) {
int res = 0;
while(n != 0){
if((n & 1) == 1) res++;
n = n >>> 1;
}
return res;
}
// n&(n−1) 解析: 二进制数字 nn 最右边的 11 变成 00 ,其余不变
public int hammingWeight2(int n){
int res = 0;
while(n != 0){
res++;
n = n & (n-1);
}
return res;
}
}
剑指 Offer 29. 顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
限制:
0 <= matrix.length <= 100
0 <= matrix[i].length <= 100
class Solution {
public int[] spiralOrder(int[][] matrix) {
if(matrix.length == 0) return new int[0];
int l = 0, r = matrix[0].length-1, t = 0, b = matrix.length-1;
int[] res = new int[(r+1) * (b+1)];
int idx = 0;
while(true){
for(int i = l; i <= r; i++) res[idx++] = matrix[t][i]; // l->r
if(++t > b) break;
for(int i = t; i <= b; i++) res[idx++] = matrix[i][r]; // t->b
if(--r < l) break;
for(int i = r; i >= l; i--) res[idx++] = matrix[b][i]; // r->l
if(--b < t) break;
for(int i = b; i >= t; i--) res[idx++] = matrix[i][l]; // b->t
if(++l > r) break;
}
return res;
}
}
剑指 Offer 11. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
示例 1:
输入:numbers = [3,4,5,1,2]
输出:1
示例 2:
输入:numbers = [2,2,2,0,1]
输出:0
提示:
n == numbers.length
1 <= n <= 5000
-5000 <= numbers[i] <= 5000
numbers 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
LeetCode
class Solution {
public int minArray(int[] numbers) {
int l = 0, r = numbers.length-1;
while(l < r){
int mid = l + (r-l) / 2;
if(numbers[mid] >= numbers[l] && numbers[mid] <= numbers[r]) l = mid;
else{}
}
return numbers[l];
}
}
From T** Test
You are given an array A of integers. Find the maximum number of non-intersecting segments of length 2 (two adjacent elements), such that segments have an equal sum.
For example, given A = [10, 1, 3, 1, 2, 2, 1, 0, 4], there are three non-intersecting segments, each whose sum is equal to 4: (1, 3), (2, 2), (0, 4). Another three non-intersecting segments are: (3,1). (2,2), (0, 4).
Write a function:
class Solution { public int solution (int[] A); }
that, given an array A of N integers, returns, the maximum number of segments with equal sums
Examples:
- Given
A = [10, 1, 3, 1, 2, 2, 1, 0, 4], the function should return 3, as explained above. - Given
A = (5, 3,1, 3, 2, 3], the function should return 1, Each sum of two adjacent elements
is different from the others. - Given
A = [19, 9, 9, 9, 9], the function should return 2. - Given
A = [1, 5,2, 4, 3, 31], the function should return 3, There are three segments:(1, 5),(2,4),(3,3)whose sums are equal to 6.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [2..100,000];
- each element of array A is an integer within the range [0... 1,000,000,000].
int solution2(int[] a) {
Map<Integer, Integer> record = new HashMap<>();
int beforeSum = -1;
int max = 0;
int cnt;
for (int i = 0; i < a.length - 1; i++) {
int sum = a[i] + a[i + 1];
if (sum == beforeSum) {
beforeSum = -1;
} else {
if (record.containsKey(sum)) {
cnt = record.get(sum) + 1;
record.put(sum, cnt);
} else {
cnt = 1;
record.put(sum, cnt);
}
max = Math.max(max, cnt);
beforeSum = sum;
}
}
return max;
}