2018年12月25&26日
小结:昨天因为整理课件,调代码耗费了大量时间,所以没来得及整理作业,这两天主要做的题目是关于树链剖分和线段树的,难度大约都是省选难度,毕竟只要涉及到树链剖分难度就肯定不低。
一. 完成的题目:
洛谷P3870,洛谷P2628,洛谷P3384,洛谷P2590,洛谷P3178,洛谷P2014,洛谷P4092,SP1716
二.
1. 完成题目数:8道。
2. 未完成6个题目的原因:
3. 复习的知识点:树链剖分,树型dp,dfs序,线段树
4.不会题目:SP6779,洛谷P1823
三:
1.洛谷 P3870 [TJOI2009]开关
题目描述
现有\(N(2 ≤ N ≤ 100000)\)盏灯排成一排,从左到右依次编号为:\(1,2,......,N\)。然后依次执行\(M(1 ≤ M ≤ 100000)\)项操作,操作分为两种:第一种操作指定一个区间\([a, b]\),然后改变编号在这个区间内的灯的状态(把开着的灯关上,关着的灯打开),第二种操作是指定一个区间\([a, b]\),要求你输出这个区间内有多少盏灯是打开的。灯在初始时都是关着的。
输入输出格式
输入格式:
第一行有两个整数\(N\)和\(M\),分别表示灯的数目和操作的数目。接下来有\(M\)行,每行有三个整数,依次为:\(c, a, b\)。其中\(c\)表示操作的种类,当\(c\)的值为\(0\)时,表示是第一种操作。当\(c\)的值为\(1\)时表示是第二种操作。\(a\)和\(b\)则分别表示了操作区间的左右边界\((1 ≤ a ≤ b ≤ N)\)。
输出格式:
每当遇到第二种操作时,输出一行,包含一个整数:此时在查询的区间中打开的灯的数目。
输入输出样例
输入样例#1:
4 5
0 1 2
0 2 4
1 2 3
0 2 4
1 1 4
输出样例#1:
1
2
思路:还是一道线段树区间异或,思路跟之前做的洛谷P2574和洛谷P2846完全一样。
代码:
#include<cstdio>
#include<cctype>
#define maxn 100007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int n,m,sum[maxn<<2],lazy[maxn<<2];
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';
return num*f;
}
inline void pushup(int rt) {
sum[rt]=sum[ls]+sum[rs];
}
inline void pushdown(int rt, int len) {
if(lazy[rt]) {
lazy[ls]^=1;
lazy[rs]^=1;
sum[ls]=(len-(len>>1))-sum[ls];
sum[rs]=(len>>1)-sum[rs];
lazy[rt]=0;
}
}
void modify(int rt, int l, int r, int L, int R) {
if(L>r||R<l) return;
if(L<=l&&r<=R) {
lazy[rt]^=1;
sum[rt]=r-l+1-sum[rt];
return;
}
pushdown(rt,r-l+1);
int mid=(l+r)>>1;
modify(ls,l,mid,L,R),modify(rs,mid+1,r,L,R);
pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
if(L>r||R<l) return 0;
if(L<=l&&r<=R) return sum[rt];
pushdown(rt,r-l+1);
int mid=(l+r)>>1;
return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
int main() {
n=qread(),m=qread();
for(int i=1,k,l,r;i<=m;++i) {
k=qread(),l=qread(),r=qread();
if(!k) modify(1,1,n,l,r);
else printf("%d\n",csum(1,1,n,l,r));
}
return 0;
}
2. 洛谷 P2826 LJJ的数学课
题目背景
题目描述(本题是提高组第二题难度+)
题目描述
LJJ又要开始上数学课啦!(T1,永恒不变的数学)
LJJ的Teacher对上次的考试很不满意(其实是出题人对上次的分数那么高不满意啦),决定在出一道难(water)题。
LJJ的Teacher给了LJJ一个数列,但这由于是LJJ的Teacher发明的,我们不称呼他为LJJ数列,而称他为Teacher数列。但是LJJ还停留在数数的阶段啊,所以不能太难。
于是LJJ的Teacher随便给出了一个Teacher数列。
Teacher会对这个数列进行两个操作:
1:将其中的一个数加上s(s为整数)
2:Teacher会给出left和right,让你求:
a[left](right-left+1) + a[left+1](right-left)
- ...... + a[right-1]2 + a[right]1 的值。
即 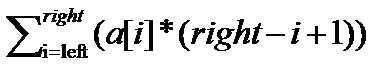
LJJ的指头掰不过来了呀,就请您来完成啦~
输入输出格式
输入格式:
第一行有2个数n,q,分别表示Teacher数列中数的个数以及操作次数。
接下来的一行有n个数,第i个数表示a[i]。
再接下来q行,每行三个数;第一个数是order。如果order=1,那么接下来两个数:x, s,即把a[x]加上s;如果order=2,那么接下来两个数:left, right,即求这一段区间ljj要求的答案。
注意:Teacher数列中的数并不一定都是正数,但一定都是整数。
输出格式:
对于每一个询问(order=2)输出所求答案
输入输出样例
输入样例#1:
5 3
2 4 1 3 5
2 2 4
1 2 3
2 2 4
输出样例#1:
17
26
说明
数据范围
n<=100000, q<=100000,保证答案不超过long long (int64) 范围,保证数据有梯度
样例解释
43+12+3*1=17
73+12+3*1=26
提示 1.如果看不懂题目,那么看这里:给你一段数列,有两种操作,单点修改和区间查询。查询left到right,返回的值是
a[left](right-left+1)+a[left+1](right-left)+...+a[right]*1。
2.从另一个角度去想问题,把区间答案划分开来,否则你会打得很累。
3.题目中说是单点修改,而不是区间修改,有没有觉得简单得不可思议呢?
思路:把题目给的式子化一化,提出后面的right-1,变成\(a_{i}*(right+1)-a_{i}*i\),整个式子变成\(\sum_{}(a_{i}*(right+1)-a_{i}*i)\),用树状数组所以维护\(a_{i}*i\)和普通的加法和就好了。
代码:
#include<cstdio>
#include<cctype>
#define maxn 100007
#define lb(x) x&(-x)
#define ll long long
using namespace std;
ll n,m,a[maxn],b[maxn];
inline ll qread() {
char c=getchar();ll num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';
return num*f;
}
inline void add(ll x, ll w) {
ll p=x*w;
while(x<=n) {
a[x]+=w;
b[x]+=p;
x+=lb(x);
}
}
inline ll csum1(ll x) {
ll ans=0;
while(x) {
ans+=a[x];
x-=lb(x);
}
return ans;
}
inline ll csum2(ll x) {
ll ans=0;
while(x) {
ans+=b[x];
x-=lb(x);
}
return ans;
}
int main() {
n=qread(),m=qread();
for(ll i=1,x;i<=n;++i) {
x=qread();
add(i,x);
}
for(ll i=1,k,l,r;i<=m;++i) {
k=qread(),l=qread(),r=qread();
if(k==1) add(l,r);
else printf("%lld\n",(r+1)*(csum1(r)-csum1(l-1))-csum2(r)+csum2(l-1));
}
return 0;
}
3. 洛谷P3384 【模板】树链剖分
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
输入样例#1:
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
输出样例#1:
2
21
说明
时空限制:1s,128M
数据规模:
对于30%的数据: N \leq 10, M \leq 10N≤10,M≤10
对于70%的数据: N \leq {10}^3, M \leq {10}^3N≤103,M≤103
对于100%的数据: N \leq {10}^5, M \leq {10}^5N≤105,M≤105
( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:

各个操作如下:

故输出应依次为2、21(重要的事情说三遍:记得取模)
思路:思路在课件里面写过了,不想再写一遍了……就是一个树链剖分加线段树的板子题。
代码:
#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
#define ll long long
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int mod,head[maxn],d[maxn],sum[maxn<<2],a[maxn];
int num,cnt,n,m,lazy[maxn<<2],fa[maxn],id[maxn];
int rt,w[maxn],top[maxn],size[maxn],son[maxn];
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';
return num*f;
}
struct node {
int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
e[++num].v=v;
e[num].nxt=head[u];
head[u]=num;
}
inline void pushup(int rt) {
sum[rt]=(sum[ls]+sum[rs])%mod;
}
void build(int rt, int l, int r) {
if(l==r) {
sum[rt]=a[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(rt);
}
inline void pushdown(int rt, int len) {
if(lazy[rt]) {
lazy[ls]+=lazy[rt],lazy[ls]%=mod;
lazy[rs]+=lazy[rt],lazy[rs]%=mod;
sum[ls]+=(len-(len>>1))*lazy[rt],sum[ls]%=mod;
sum[rs]+=(len>>1)*lazy[rt],sum[rs]%=mod;
lazy[rt]=0;
}
}
void modify(int rt, int l, int r, int L, int R, int val) {
if(L>r||R<l) return;
if(L<=l&&r<=R) {
sum[rt]+=val*(r-l+1),sum[rt]%=mod;
lazy[rt]+=val,lazy[rt]%=mod;
return;
}
int mid=(l+r)>>1;
pushdown(rt,r-l+1);
modify(ls,l,mid,L,R,val),modify(rs,mid+1,r,L,R,val);
pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
if(L>r||R<l) return 0;
if(L<=l&&r<=R) return sum[rt];
int mid=(l+r)>>1;
pushdown(rt,r-l+1);
return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
void dfs1(int u, int f) {
size[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=f) {
d[v]=d[u]+1;
fa[v]=u;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
}
void dfs2(int u, int t) {
id[u]=++cnt;
a[cnt]=w[u];
top[u]=t;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
int calc(int x, int y) {
int ans=0;
int fx=top[x],fy=top[y];
while(fx!=fy) {
if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
ans+=csum(1,1,cnt,id[fx],id[x]);
x=fa[fx],fx=top[x];
}
if(id[x]>id[y]) swap(x,y);
ans+=csum(1,1,cnt,id[x],id[y]);
return ans;
}
void cal(int x, int y, int val) {
int fx=top[x],fy=top[y];
while(fx!=fy) {
if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
modify(1,1,cnt,id[fx],id[x],val);
x=fa[fx],fx=top[x];
}
if(id[x]>id[y]) swap(x,y);
modify(1,1,cnt,id[x],id[y],val);
}
int main() {
n=qread(),m=qread(),rt=qread(),mod=qread();
for(int i=1;i<=n;++i) w[i]=qread(),w[i]%=mod;
for(int i=1,u,v;i<n;++i) {
u=qread(),v=qread();
ct(u,v);ct(v,u);
}
d[rt]=1,fa[rt]=1;
dfs1(rt,0);dfs2(rt,rt);build(1,1,n);
for(int i=1,k,x,y,z;i<=m;++i) {
k=qread();
if(k==1) {
x=qread(),y=qread(),z=qread();
cal(x,y,z%mod);
}
if(k==2) {
x=qread(),y=qread();
printf("%d\n",calc(x,y)%mod);
}
if(k==3) {
x=qread(),y=qread();
modify(1,1,n,id[x],id[x]+size[x]-1,y%mod);
}
if(k==4) {
x=qread();
printf("%d\n",csum(1,1,n,id[x],id[x]+size[x]-1)%mod);
}
}
return 0;
}
4. 洛谷P2590 [ZJOI2008]树的统计
题目描述
一棵树上有n个节点,编号分别为1到n,每个节点都有一个权值w。
我们将以下面的形式来要求你对这棵树完成一些操作:
I. CHANGE u t : 把结点u的权值改为t
II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值
III. QSUM u v: 询问从点u到点v的路径上的节点的权值和
注意:从点u到点v的路径上的节点包括u和v本身
输入输出格式
输入格式:
输入文件的第一行为一个整数n,表示节点的个数。
接下来n – 1行,每行2个整数a和b,表示节点a和节点b之间有一条边相连。
接下来一行n个整数,第i个整数wi表示节点i的权值。
接下来1行,为一个整数q,表示操作的总数。
接下来q行,每行一个操作,以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。
输出格式:
对于每个“QMAX”或者“QSUM”的操作,每行输出一个整数表示要求输出的结果。
输入输出样例
输入样例#1:
4
1 2
2 3
4 1
4 2 1 3
12
QMAX 3 4
QMAX 3 3
QMAX 3 2
QMAX 2 3
QSUM 3 4
QSUM 2 1
CHANGE 1 5
QMAX 3 4
CHANGE 3 6
QMAX 3 4
QMAX 2 4
QSUM 3 4
输出样例#1:
4
1
2
2
10
6
5
6
5
16
说明
对于100%的数据,保证1<=n<=30000,0<=q<=200000;中途操作中保证每个节点的权值w在-30000到30000之间。
思路:这道题目跟洛谷P3384那到题的区别在于那道题是区间修改,这道题是单点修改,这道题还多了查询任意两点最短路径上的最大点权,实际上区间修改包括单点修改,所以这道题只多用树剖维护一个路径最大点权即可。
代码:
#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 30007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int head[maxn],d[maxn],lazy[maxn<<2],sum[maxn<<2];
int maxx[maxn<<2],a[maxn],num,cnt,n,m,fa[maxn],id[maxn];
int w[maxn],top[maxn],size[maxn],son[maxn];
char s[8];
struct node {
int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
e[++num].v=v;
e[num].nxt=head[u];
head[u]=num;
}
inline void pushup(int rt) {
sum[rt]=sum[ls]+sum[rs];
maxx[rt]=max(maxx[ls],maxx[rs]);
}
void build(int rt, int l, int r) {
if(l==r) {
sum[rt]=a[l];
maxx[rt]=a[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(rt);
}
void add(int rt, int l, int r, int L, int val) {
if(l==r) {
sum[rt]=maxx[rt]=val;
return;
}
int mid=(l+r)>>1;
if(L>mid) add(rs,mid+1,r,L,val);
else add(ls,l,mid,L,val);
pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
if(L>r||R<l) return 0;
if(L<=l&&r<=R) return sum[rt];
int mid=(l+r)>>1;
return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
int cmax(int rt, int l, int r, int L, int R) {
int ans=-1020040222;
if(L>r||R<l) return 0;
if(L<=l&&r<=R) return maxx[rt];
int mid=(l+r)>>1;
if(L<=mid) ans=max(ans,cmax(ls,l,mid,L,R));
if(R>mid) ans=max(ans,cmax(rs,mid+1,r,L,R));
return ans;
}
void dfs1(int u, int f) {
size[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=f) {
d[v]=d[u]+1;
fa[v]=u;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
}
void dfs2(int u, int t) {
id[u]=++cnt;
a[cnt]=w[u];
top[u]=t;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
int calc1(int x, int y) {
int maxx=-1020040222;
int fx=top[x],fy=top[y];
while(fx!=fy) {
if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
maxx=max(maxx,cmax(1,1,cnt,id[fx],id[x]));
x=fa[fx],fx=top[x];
}
if(id[x]>id[y]) swap(x,y);
maxx=max(maxx,cmax(1,1,cnt,id[x],id[y]));
return maxx;
}
int calc2(int x, int y) {
int ans=0;
int fx=top[x],fy=top[y];
while(fx!=fy) {
if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
ans+=csum(1,1,cnt,id[fx],id[x]);
x=fa[fx],fx=top[x];
}
if(id[x]>id[y]) swap(x,y);
ans+=csum(1,1,cnt,id[x],id[y]);
return ans;
}
int main() {
scanf("%d",&n);
for(int i=1,u,v;i<n;++i) {
scanf("%d%d",&u,&v);
ct(u,v);ct(v,u);
}
for(int i=1;i<=n;++i) scanf("%d",&w[i]);
d[1]=1,fa[1]=1;
dfs1(1,0);dfs2(1,1);build(1,1,n);
scanf("%d",&m);
for(int i=1,x,y;i<=m;++i) {
scanf("%s%d%d",s,&x,&y);
if(s[1]=='H') add(1,1,n,id[x],y);
if(s[1]=='M') printf("%d\n",calc1(x,y));
if(s[1]=='S') printf("%d\n",calc2(x,y));
}
return 0;
}
5. 洛谷P3178 [HAOI2015]树上操作
题目描述
有一棵点数为 N 的树,以点 1 为根,且树点有边权。然后有 M 个操作,分为三种:
- 操作 1 :把某个节点 x 的点权增加 a 。
- 操作 2 :把某个节点 x 为根的子树中所有点的点权都增加 a 。
- 操作 3 :询问某个节点 x 到根的路径中所有点的点权和。
输入输出格式
输入格式:
第一行包含两个整数 N, M 。表示点数和操作数。
接下来一行 N 个整数,表示树中节点的初始权值。
接下来 N-1 行每行两个正整数 from, to , 表示该树中存在一条边 (from, to) 。
再接下来 M 行,每行分别表示一次操作。其中第一个数表示该操作的种类( 1-3 ) ,之后接这个操作的参数( x 或者 x a ) 。
输出格式:
对于每个询问操作,输出该询问的答案。答案之间用换行隔开。
输入输出样例
输入样例#1:
5 5
1 2 3 4 5
1 2
1 4
2 3
2 5
3 3
1 2 1
3 5
2 1 2
3 3
输出样例#1:
6
9
13
说明
对于 100% 的数据, N,M<=100000 ,且所有输入数据的绝对值都不会超过 10^6 。
思路:这道题跟洛谷P3384的唯一区别在于这里是单点修改,上面说过,区间修改包括单点修改,所以,可是说是一点区别都没有,就是打一遍加深一下对树剖的印象。
代码:
#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
#define ll long long
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int head[maxn],d[maxn],a[maxn];
int num,cnt,n,m,fa[maxn],id[maxn];
int w[maxn],top[maxn],size[maxn],son[maxn];
ll lazy[maxn<<2],sum[maxn<<2],y;
inline ll qread() {
char c=getchar();ll num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';
return num*f;
}
struct node {
int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
e[++num].v=v;
e[num].nxt=head[u];
head[u]=num;
}
inline void pushup(int rt) {
sum[rt]=sum[ls]+sum[rs];
}
void build(int rt, int l, int r) {
if(l==r) {
sum[rt]=a[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(rt);
}
inline void pushdown(int rt, int len) {
if(lazy[rt]) {
lazy[ls]+=lazy[rt];
lazy[rs]+=lazy[rt];
sum[ls]+=(len-(len>>1))*lazy[rt];
sum[rs]+=(len>>1)*lazy[rt];
lazy[rt]=0;
}
}
void modify(int rt, int l, int r, int L, int R, ll val) {
if(L>r||R<l) return;
if(L<=l&&r<=R) {
sum[rt]+=val*(r-l+1);
lazy[rt]+=val;
return;
}
int mid=(l+r)>>1;
pushdown(rt,r-l+1);
modify(ls,l,mid,L,R,val),modify(rs,mid+1,r,L,R,val);
pushup(rt);
}
ll csum(int rt, int l, int r, int L, int R) {
if(L>r||R<l) return 0;
if(L<=l&&r<=R) return sum[rt];
int mid=(l+r)>>1;
pushdown(rt,r-l+1);
return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
void dfs1(int u, int f) {
size[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=f) {
d[v]=d[u]+1;
fa[v]=u;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
}
void dfs2(int u, int t) {
id[u]=++cnt;
a[cnt]=w[u];
top[u]=t;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
ll calc(int x, int y) {
ll ans=0;
int fx=top[x],fy=top[y];
while(fx!=fy) {
if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
ans+=csum(1,1,cnt,id[fx],id[x]);
x=fa[fx],fx=top[x];
}
if(id[x]>id[y]) swap(x,y);
ans+=csum(1,1,cnt,id[x],id[y]);
return ans;
}
int main() {
n=qread(),m=qread();
for(int i=1;i<=n;++i) w[i]=qread();
for(int i=1,u,v;i<n;++i) {
u=qread(),v=qread();
ct(u,v);ct(v,u);
}
d[1]=1,fa[1]=1;
dfs1(1,0);dfs2(1,1);build(1,1,n);
for(int i=1,k,x;i<=m;++i) {
k=qread();
if(k==1) {
x=qread(),y=qread();
modify(1,1,n,id[x],id[x],y);
}
if(k==2) {
x=qread(),y=qread();
modify(1,1,n,id[x],id[x]+size[x]-1,y);
}
if(k==3) {
x=qread();
printf("%lld\n",calc(1,x));
}
}
return 0;
}
6. 洛谷 P2014 选课
题目描述
在大学里每个学生,为了达到一定的学分,必须从很多课程里选择一些课程来学习,在课程里有些课程必须在某些课程之前学习,如高等数学总是在其它课程之前学习。现在有N门功课,每门课有个学分,每门课有一门或没有直接先修课(若课程a是课程b的先修课即只有学完了课程a,才能学习课程b)。一个学生要从这些课程里选择M门课程学习,问他能获得的最大学分是多少?
输入输出格式
输入格式:
第一行有两个整数N,M用空格隔开。(1<=N<=300,1<=M<=300)
接下来的N行,第I+1行包含两个整数ki和si, ki表示第I门课的直接先修课,si表示第I门课的学分。若ki=0表示没有直接先修课(1<=ki<=N, 1<=si<=20)。
输出格式:
只有一行,选M门课程的最大得分。
输入输出样例
输入样例#1:
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
输出样例#1:
13
思路:数据范围也不是特别大,可以考虑树型dp,首先,建图就是按照题目所给的信息建有向边,之后我们用f[i][j]表示以i为顶点,选了j门课程的最大得分,然后dfs时枚举每条与一个点相连的边,用这个结点去更新它的子节点为顶点时的初始值,然后遍历完它所有的子节点之后,再回过头来更新这个结点为顶点时的最大值。
代码:
#include<cstdio>
#include<algorithm>
#define maxn 307
using namespace std;
int n,m,head[maxn],f[maxn][maxn],w[maxn],num;
struct node {
int v,nxt;
}e[maxn];
inline void ct(int u, int v) {
e[++num].v=v;
e[num].nxt=head[u];
head[u]=num;
}
void dfs(int u, int k) {
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
for(int j=k+1;j<=m+1;++j) f[v][j]=f[u][j-1]+w[v];
dfs(v,k+1);
for(int j=k+1;j<=m+1;++j) f[u][j]=max(f[u][j],f[v][j]);
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u;i<=n;++i) {
scanf("%d%d",&u,&w[i]);
ct(u,i);
}
dfs(0,1);
printf("%d\n",f[0][m+1]);
return 0;
}
7. 洛谷P4092 [HEOI2016/TJOI2016]树
题目描述
在2016年,佳媛姐姐刚刚学习了树,非常开心。现在他想解决这样一个问题:给定一颗有根树(根为1),有以下两种操作:
-
标记操作:对某个结点打上标记(在最开始,只有结点1有标记,其他结点均无标记,而且对于某个结点,可以打多次标记。)
-
询问操作:询问某个结点最近的一个打了标记的祖先(这个结点本身也算自己的祖先)
你能帮帮他吗?
输入输出格式
输入格式:
输入第一行两个正整数N和Q分别表示节点个数和操作次数
接下来N-1行,每行两个正整数u,v(1≤u,v≤n)表示u到v有一条有向边
接下来Q行,形如“opernum”oper为“C”时表示这是一个标记操作,oper为“Q”时表示这是一个询问操作对于每次询问操作。
输出格式:
输出一个正整数,表示结果
输入输出样例
输入样例#1:
5 5
1 2
1 3
2 4
2 5
Q 2
C 2
Q 2
Q 5
Q 3
输出样例#1:
1
2
2
1
说明
30%的数据,1 ≤ N, Q ≤ 1000
70%的数据,1 ≤ N, Q ≤ 10000
100%的数据,1 ≤ N, Q ≤ 100000
思路:题意就是让你设计一个数据结构,支持:
- 单点修改:加标记。
- 询问操作:询问某个结点最近的一个打了标记的祖先(自己也算自己的祖先)。
单点修改就不用说了吧,对于操作2,我们发现离某个结点最近的一个打了标记的祖先就是树剖时第二遍dfs的id值大的那个祖先(前提是打过标记),然后树链剖分,用线段树维护最大值。
代码:
#include<cstdio>
#include<algorithm>
#define maxn 100007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int cnt,n,m,head[maxn],num,size[maxn],d[maxn];
int id[maxn],maxx[maxn<<2],son[maxn],fa[maxn];
int a[maxn],top[maxn];
char c[3];
struct node {
int v,nxt;
}e[maxn<<2];
inline void ct(int u, int v) {
e[++num].v=v;
e[num].nxt=head[u];
head[u]=num;
}
void dfs1(int u, int f) {
size[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=f) {
d[v]=d[u]+1;
fa[v]=u;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]]) son[u]=v;
}
}
}
void dfs2(int u, int t) {
id[u]=++cnt;
top[u]=t;
a[cnt]=u;
if(son[u]) dfs2(son[u],t);
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void pushup(int rt) {
maxx[rt]=max(maxx[ls],maxx[rs]);
}
void add(int rt, int l, int r, int val) {
if(l==r) {
maxx[rt]=val;
return;
}
int mid=(l+r)>>1;
if(val>mid) add(rs,mid+1,r,val);
else add(ls,l,mid,val);
pushup(rt);
}
int cmax(int rt, int l, int r, int L, int R) {
if(L>r||R<l) return 0;
if(L<=l&&r<=R) return maxx[rt];
int ans=0;
int mid=(l+r)>>1;
if(L<=mid) ans=max(ans,cmax(ls,l,mid,L,R));
if(R>mid) ans=max(ans,cmax(rs,mid+1,r,L,R));
return ans;
}
int query(int x, int y) {
int maxx=0;
int fx=top[x],fy=top[y];
while(fx!=fy) {
if(d[fx]<d[fy]) swap(x,y),swap(fx,fy);
maxx=max(maxx,cmax(1,1,cnt,id[fx],id[x]));
x=fa[fx],fx=top[x];
}
if(id[x]>id[y]) swap(x,y);
maxx=max(maxx,cmax(1,1,cnt,id[x],id[y]));
return a[maxx];
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<n;++i) {
scanf("%d%d",&u,&v);
ct(u,v);ct(v,u);
}
d[1]=1;dfs1(1,0);dfs2(1,1);
add(1,1,n,id[1]);
for(int i=1,x;i<=m;++i) {
scanf("%s%d",c,&x);
if(c[0]=='C') add(1,1,n,id[x]);
else printf("%d\n",query(x,1));
}
return 0;
}
8. SP1716 GSS3
题意翻译
n 个数,q 次操作
操作0 x y把\(A_x\) 修改为y
操作1 l r询问区间[l, r][l,r] 的最大子段和
输入输出格式
输入格式:
The first line of input contains an integer N. The following line contains N integers, representing the sequence A1..AN.
The third line contains an integer M. The next M lines contain the operations in following form:
0 x y: modify Ax into y (|y|<=10000).
1 x y: print max{Ai + Ai+1 + .. + Aj | x<=i<=j<=y }.
输出格式:
For each query, print an integer as the problem required.
输入输出样例
输入样例#1:
4
1 2 3 4
4
1 1 3
0 3 -3
1 2 4
1 3 3
输出样例#1:
6
4
-3
思路:首先分析询问的本质:求出区间最大子段和!很显然我们可以使用线段树维护序列,本题的难点主要在如何进行上传操作,将子树l和r的节点信息上传到子树rt时,对于rt维护的序列中,和最大的子段有两种情况:
- 子段不经过中点,那么 rt 的答案为 l 和 r 的答案的最大值。
- 子段经过了中点。这种情况比较复杂,因为我们无法知道子树的答案所对应的序列。这也是本题的难点所在。
然后我们用结构体板线段树来分情况维护一下最大字段和即可,结构体传址快。
代码:
#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 50007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
inline int qread() {
char c=getchar();int num=0,f=1;
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) num=num*10+c-'0';
return num*f;
}
int n,m;
struct Tree {
int lmax,rmax,sum,maxx;
}tree[maxn<<2];
inline void pushup(int rt) {
tree[rt].lmax=max(tree[ls].lmax,tree[ls].sum+tree[rs].lmax);
tree[rt].rmax=max(tree[rs].rmax,tree[rs].sum+tree[ls].rmax);
tree[rt].maxx=max(tree[ls].rmax+tree[rs].lmax,max(tree[ls].maxx,tree[rs].maxx));
tree[rt].sum=tree[ls].sum+tree[rs].sum;
}
void build(int rt, int l, int r) {
if(l==r) {
tree[rt].lmax=tree[rt].rmax=tree[rt].sum=tree[rt].maxx=qread();
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(rt);
}
void add(int rt, int l, int r, int L, int val) {
if(l==r) {
tree[rt].lmax=tree[rt].rmax=tree[rt].sum=tree[rt].maxx=val;
return;
}
int mid=(l+r)>>1;
if(L<=mid) add(ls,l,mid,L,val);
else add(rs,mid+1,r,L,val);
pushup(rt);
}
Tree query(int rt, int l, int r, int L, int R) {
if(L==l&&r==R) return tree[rt];
int mid=(l+r)>>1;
if(L>mid) return query(rs,mid+1,r,L,R);
else if(R<=mid) return query(ls,l,mid,L,R);
else {
Tree a=query(ls,l,mid,L,mid),b=query(rs,mid+1,r,mid+1,R),c;
c.lmax=max(a.lmax,a.sum+b.lmax);
c.rmax=max(b.rmax,b.sum+a.rmax);
c.sum=a.sum+b.sum;
c.maxx=max(a.rmax+b.lmax,max(a.maxx,b.maxx));
return c;
}
}
int main() {
n=qread();
build(1,1,n);
m=qread();
for(int i=1,k,x,y;i<=m;++i) {
k=qread(),x=qread(),y=qread();
if(!k) add(1,1,n,x,y);
else printf("%d\n",query(1,1,n,x,y).maxx);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号