算法导论——动态规划

　　动态规划指的是一个问题可以拆分成多个小的最优子问题，并且这些子问题具有重叠，典型的如斐波那契数列：f(2)=f(1)+f(0),f(3)=f(2)+f(1),f(4)=f(3)+f(2)，若使用简单的递归算法求f(4)，则f(2)会被计算两次，当计算f(n)时需要计算f(n-1)和f(n-2)而f(n-1)又要计算记一次f(n-2)，如此往复时间复杂度为n的指数级别，导致算法效率低下。若能够记录f(2)至f(n-1)的结果，可以保证每一级计算都是O(1)复杂度，整个算法的时间复杂度就能下降至O(n)，空间复杂度O(n)。必须保证拆分后的子问题是当前规模下的最优解，才可保证递归逻辑的正确，典型的例子是无权最短路径问题，若已知A到除最终目的地B外的所有点最短路径，则只需遍历寻找与B直接相邻所有点到A最近的一个。

通常动态规划可以分为4个步骤：

1. 刻画一个最优解的结构特征
2. 递归地定义最优解的值
3. 计算最优解的值，通常采用自底向上的方法
4. 利用计算出的信息构造一个最优解

因此，动态规划的关键是分析子问题的拆分与递归式。下面四个问题来自《算法导论》第三版。

钢条切割

　　有一条长度为n的钢条，可以不计成本的切割成多条钢条出售，不同长度与价格关系如下表所示，求如何切割获得最大的利益r_n

长度i	1	2	3	4	5	6	7	8	9	10
价格pi	1	5	8	9	10	17	17	20	24	30

以长度n=4为例，分割共有以下几种方案

n=4, r=9

n=1+3, r=9

n=1+1+2, r=7

n=1+1+1+1, r=4

n=2+2, r=10

最佳方案为分成2+2两端，利润为10

 

　　对于长度为n的钢条，其可以通过切割获得的最大利益记为r_n，r_n=max(p_n,r₁+r_n-1,r₂+r_n-2,...r_n-1+r₁) r_n的最大利润可能有两种情况：不切割或者先切为两段，该两段各自的r_i+r_n-i为最大值。因此可以采用递归的方式，求出r_n的值，伪代码如下：

int cutRod(p,n){
    if(n==0)
        return 0;
    q=-1
    for(i=1;i<=n;i++){
        q=max(q,p[i]+cutRod(p,n-i));
    }
    return q;
}

　　该算法的问题是效率太低，原因在于cutRod(p,i)这个值在不同阶段被分别计算了多次，比如要求长度为2的钢条的最大利益，要计算分割成1+1的利益，这里r₁被计算了两次。如果能够记录r₁到r_n-1的值，可以大幅度提交计算效率，这是一种典型的空间换取时间的方法——动态规划算法。

动态规划有两种等价的实现方法：

　　第一种，带备忘的自顶向下法。在之间递归算法调用每一层的时候，先检查该值有没有被计算过，若没有，调用并存储；若计算过，直接取出该值。伪代码如下：

int memoizedCutRod(p,n){
    r[n+1] //用于记录r0到rn-1的值
    for(i=0;i<=n;i++){
        r[i]=-1;
    }
    return memoizedCutRodAux(p,n,r);
}

int memoizedCutRodAux(p,n,r){
    if(r[n]>=0)
        return r[n];
    if(n==0)
        q=0;
    else
    {
        q=-1;
        for(i=0;i<=n;i++){
            q=max(q,p[i]+ memoizedCutRodAux(p,n-i,r));
        }
    }
    r[n]=q;
    return q;
}

　　第二种，自底向上法，将一个问题分成规模更小的子问题，从小到大进行求解，当求解至原问题时，所需的值都已求解完毕。对于分割铁棒问题来说，从长度为1一直求解至长度为n时最佳分割方案的收益。由于r_n=max(p_n,r₁+r_n-1,r₂+r_n-2,...r_n-1+r₁)，只需计算出r₁至r_n-1的值，便可计算出r_n的值。伪代码如下：

int bottomUpCutRod(p,n){
    r[n+1] //用于记录r0到rn-1的值
    s[n+1]//若要输出分割长度，则需要记录不同长度最大利润的分割情况
    r[0]=0;
    for(j=1;j<=n;j++){
        q=-1;
        for(i=1;i<=j;i++){
            //针对长度为j时，遍历所有的分割情况，寻找到最佳的结果
            if(p[i]+r[j-i]>q){
                q= p[i]+r[j-i];
                s[j]=i;//记录分割位置
            }
        }
        r[j]=q;
    }
    return r[n];
}
void printCutRod(s,n){
    if(s[n]!=0)
        printCutRod(s,s[n]);
    printf("%d ",s[n]);//此处输出的为所有的分割位置
}

矩阵链乘法

　　矩阵相乘是符合结合律的， A1A2A3= A1(A2A3)，但是两者的计算规模可能是不同的。假设三个矩阵的大小分别是 10*100、100*5、 5*50，则 A1A2A3的计算次数为 10*100*5+10*5*50=7500，而 A1(A2A3)的计算规模为 100*5*50+10*100*50=75000，两者相差了 10 倍的规模。对于一组给定的矩阵相乘A1A2A3 ⋯ An要求出如何进行乘法结合可以进行最少的计算次数。

　　下面使用形如A1∗n来表示A1A2A3 ⋯ An的最终乘积结果。对于A1∗n的最少计算式，其必定在Ak 处进行了分割 (A1A2A3 ⋯ Ak)(Ak+1Ak+2 ⋯ An)，总计算次数为 m,i, j- = min{m,i, k- +m,k + 1, j- + pi−1pkpj}, i ≤ k < j，故必须要先求出A1A2A3 ⋯ Ak和Ak+1Ak+2 ⋯ An各自的最少计算次数然后遍历计算出最小值。 因此可以采用自 1 int matrixChainOrder(p){

    n=p.length-1;
    m[n][n],s[n][n];//m记录矩阵链各自的最少计算次数,s记录最少时分割位置
    for(i=0;i<=n;i++)
        m[i][i]=0;
    for(l=2;l<=n;l++){//l限制矩阵链的长度，先计算出所有2个矩阵相乘的最少次数，然后是3个矩阵，直至n个矩阵
        for(i=1;i<=n-l+1;i++){
            j=i+l-1;
            m[i][j]=INFI;
            // m[i,j]=min{m[i,k]+m[k+1,j]+p_(i-1) p_k p_j },i≤k<j
            for(k=i;k<=j-1;k++){
                q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
                if(q<m[i][j]){
                    m[i][j]=q;
                    s[i][j]=k;
                }
            }
        }
    }
    //此处可添加打印分割结果的代码
    return m[n];
对于X = x1x2 ⋯ xm和Y = y1y2 ⋯ yn的 LCS 记为Z = z1z2 ⋯ zk最优子结构拆分：

1. 如果xm = yn，则zk = xm = yn且Zk−1是Xm−1和Yn−1的一个 LCS
2. 如果xm ≠ yn且zk ≠ xm，则 Z 是Xm−1和 Y 的一个 LCS
3. 如果xm ≠ yn且zk ≠ yn，则 Z 是 X 和Yn−1的一个 LCS
用 c[i, j] 表 示XiYj 的 LCS 长 度 ， 可 列 出 递 归 式

int lcsLength(X,Y){
    m=X.length;
    n=Y.length;
    b[m][n];//记录最优解的构造
    c[m+1][n+1];
    for(i=1;i<=m;i++)
        c[i][0]-0;
    for(j=0;j<=n;j++)
        c[0][j]=0;
    for(i=1;i<=m;i++){
        for(j=1;j<=n;j++){
            if(x[i]==y[i]){
                c[i][j]=c[i-1][j-1]+1;
                b[i][j]="↖";
            }
            else if(c[i-1][j]>=c[i][j-1]){
                c[i][j]=c[i-1][j];
                b[i][j]="↑";
            }
            else{
                c[i][j]=c[i][j-1];
                b[i][j]="←";
            }
        }
    }
    printLcs(b,X,m,n);
    return c[n];
}

void printLcs(b,X,i,j){
    if(i==0||j==0)
        return;
    if(b[i][j]=="↖"){
        printLcs(b,X,i-1,j-1);
        print x[i];
        return;
    }
    if(b[i][j]=="↑"){
        printLcs(b,X,i-1,j);
        return;
    }
    printLcs(b,X,i,j-1);
}

最优二叉搜索树

对于搜索树来说，不同节点的搜索频率是不同的，节点离根越远搜索时间就越长，所以我们希望将搜索频率高的节点放在离根近的位置，使得整体的效率期望值最优。但是，并不是简单地把搜索频率最高的点做根节点就行了，其余节点的深度增加反而可能导致整体效率降低，极端情况最小值搜索频率最高，若作为根节点，整棵树的平衡性很差，反而容易导致搜索效率的降低。

对于一个二叉搜索树，有n个关键字k₁,k₂,...,k_n和n+1个伪关键字d₀,d₁,d₂,...d_n，其中d₀代表小于k₁的搜索结果，d₁是大于k₁小于k₂的搜索结果，搜索k是成功的搜索，而搜索d是失败的搜索，所以d一定是叶子节点且d_i和d_i-1一定是k_i的两个子节点。对这样节点的最优二叉搜索树来说，他含有根节点和两棵子树，包含连续的关键字k_i,k_i+1,...,k_j和对应的伪关键字，该子树必定是对应规模的最优二叉搜索树，否则只需将该规模下的最优二叉搜索树替换该子树就会产生搜索期望值更小的树，这与最优二叉树的假设矛盾。对于特殊情况j=i-1时，树不包含实际关键字，仅含有伪关键字d_i-1。p为关键字的搜过概率，q为伪关键字的搜索概率，对于一般情况，需要从k_i,k_i+1,...,k_j中选择根节点k_r来构造最优二叉搜索树。当该树成为目标结果的子树时，因在子树的期望值基础上增加所有点的概率之和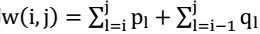，因为每个点的深度都增加了1。对于给点的节点条件，只需寻找到使左右子树的期望值加上所有节点概率之和最小即为最优二叉搜索树（左右子树所有节点加上根节点的权是1），因此可以对期望搜索代价列出递归式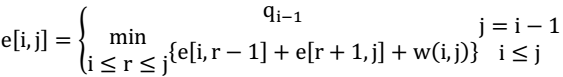

double optimal-bst(p,q,n){
    e[n+2][n+1];//e[1..n+1][0..n]记录期望值
    w[n+2][n+1];//w[1..n][0..n]记录i到j的概率和避免重复计算
    root[n+1][n+1];//root[1..n][1..n]记录所有树的根节点
    for(i=1;i<=n+1;i++){
        //初始化j=i-1的特殊情况
        e[i][i-1]=q[i-1];
        w[i][i-1]=q[i-1];
    }
    for(l=1;l<=n;l++){//l表示关键字的个数，先计算1个实际关键字的树，然后2个依次增加
        for(i=1;i<=n-l+1;i++){
            j=i+l-1;
            e[i][j]=INFI;
            w[i][j]=w[i][j-1]+p[i]+q[j];//计算w[i][j]
            for(r=i;r<=j;r++){
                t=e[i][r-1]+e[r+1][j]+w[i][j];//计算e[i,r-1]+e[r+1,j]+w(i,j)
                if(t<e[i][j]){
                    e[i][j]=t;
                    root[i][j]=r;
                }
            }
        }
    }
    //省略了打印代码
    return e[1][n];
}