整理一些定理和公式
二项式反演公式:
这个形式高度对称,它还有一个等价形式比较常用
还有一个形式
错排公式
错排问题又称伯努利错装信封问题。这个问题有很多不同的题面,下面是其中一种
伯努利错装信封问题
有一个粗心的邮差让\(n\)封信从信封中掉了出来,但他并不知道每一封信对应着哪一个信封。不负责任的他随机地把信胡乱塞进信封里。问一共有多少种装信的方案使得信全部装进了不同的信封。
我们记错排数为\(\{D_n\}\),表示将n封信全部装错方案数量,利用二项式公式可推得
第一类斯特林数
\(\left[ \begin{matrix} n\\k \end{matrix} \right]\)表示将n个数的序列划分为k个圆排列的方案数
\(\left[ \begin{matrix} n\\k \end{matrix} \right]=\left[ \begin{matrix} n-1\\k-1 \end{matrix} \right]+\left[ \begin{matrix} n-1\\k \end{matrix} \right]*(n-1)\)
\(x^{n \downarrow}=x(x-1)(x-2)\dots(x-n+1)=\sum\limits^{n}_{k=0}S_s(n,k)x^k\)
\(x^{n \uparrow}=x(x+1)(x+2)\dots(x+n-1)=\sum\limits^{n}_{k=0}S_u(n,k)x^k\)
对于有无符号Stirling数之间的关系有
\(S_s(n,m)=(-1)^{n+m}S_u(n,m)\)
。组合数学中的第一类Stirling数一般指无符号的第一类Stirling数。意思是n个不同元素构成m个圆排列的方案数。
第二类斯特林数
将\(n\)个不同的球放进\(m\)个不同的盒子,保证盒子非空,求方案数。
记\(n\)个不同的球放进\(m\)个不同的盒子里的方案总数为\(Q^m_{n}\)
同样可以利用二项式反演公式可得
第二类斯特林数指的是将\(n\)个不同的球放进\(m\)个无差别的盒子,保证盒子非空,求方案数。
只要将有差别的\(Q^m_n\)除以盒子的排列数\(m!\)就是答案,即有第二类斯特林数\(S^m_n\):
性质
左边表示k个球任意放在n个盒子中,右边枚举非空盒子数量i,把k个球放在i个盒子中(盒子不同),里面再乘上选出i个非空盒子的方案数
贝尔数
定义
第n个贝尔数表示集合{1,2,3,...,n}的划分方案数
\(B[0]=1\)
性质
递推公式为\(B_{n+1}=\sum^n_{k=0}C^k_nB_k\)
每个贝尔数都是第二类斯特林数的和
\(B_n=\sum^n_{k=1}S(n,k)\)
适合Touchard同余,对任意质数p
\(B_{p+n}=B_n+B_{n+1}(mod ~~p)\)
贝尔数的指数母函数
\(\sum^{\infty}_{n=0}\frac{B_n}{n!}x^n=e^{e^x-1}\)
期望线性性
对于任意两个随机事件x,y(x,y不要求相互独立)满足
即两个(或多个)随机变量的和的期望等于期望的和
Min-Max容斥
给定集合\(S\),设\(max(S)\)为\(S\)中的最大值,\(min(S)\)为\(S\)中的最小值,则我们有一个式子:
如果是k-thMax的话
裴蜀定理(或贝祖定理
\(ax+by=c,x\in Z^*,y\in Z^*\)成立的充分条件是\({\gcd(a,b)|c}\)
exgcd中会用到
两个互质的正整数不能凑出来的最大整数是a*b-a-b
n个整数之间的裴蜀定理
设\(a_1,a_2,a_3......a_n\)为\(n\)个整数,d是它们的gcd,那么存在整数\(x_1......x_n\)使得\(x_1*a_1+x_2*a_2+...x_n*a_n=d\)。
特别来说,如果\(a_1...a_n\)互质(不是两两互质),那么存在整数\(x_1......x_n\)使得\(x_1*a_1+x_2*a_2+...x_n*a_n=1\)证法类似两个数的情况
费马小定理
若p为质数,且a,b互质那么\(a^{p-1}\equiv1(mod p)\)
那么\(a^{p-1}(mod p)就是a在modm下的逆元了\)
欧拉定理
当a,p互质时,\(a^{\varphi(p)}\equiv1(mod p)\)
\(a^b=a^{b~mod~\phi(p)}\)
其中\(\varphi(p)\)是欧拉函数\((1\)~\(p)\)与\(p\)互质的数
那么显然费马小定理就是欧拉定理的特殊情况
求逆元和上面同理
欧拉函数的一些性质
\(\varphi(1)=1\)
对于素数p,\(\varphi(p)=p-1\)
小于n并与n互质的数的和为:\(n*\varphi(n)/2\)
欧拉定理:如果a与n互质,\(a^{\varphi(n)}mod~p=1~mod~p\)
如果m与n互质,\(\varphi(mn)= \varphi(m)*\varphi(n)\)
如果p为素数,\(\varphi(p^k) = p^k - p^{k-1}= (p-1)*p^{k-1}\)(除p的倍数外,其他数都与p互质)
\(\sum_{d|n}\varphi(d)=n\)
拓展欧拉定理
若 \(b<\varphi(m),a^b\equiv a^b(mod m)\)
若 \(b≥\varphi(m),a^b\equiv a^{bmod \varphi(m)+\varphi(m)}(mod m)\)
欧拉降幂
\(a^b\equiv a^{b\%\varphi(m)},gcd(a,m)=1\)
\(若a,m不互质\)
若 \(b<\varphi(m),a^b\equiv a^b(mod m)\)
若 \(b≥\varphi(m),a^b\equiv a^{bmod \varphi(m)+\varphi(m)}(mod m)\)
霍尔定理内容
霍尔定理是判断二分图是否满足完美匹配的充要条件,要求\(|X|=|Y|\),其中\(X\)是左边的点数,\(Y\)是右边的点数,
对于任意的\(|X|\)的子集\(a\)都有\(|a|\leq|b|\),其中\(b\)是\(a\)能匹配的点集的并,即对应\(X\)中的子集\(W\),令\(N(W)\)为\(W\)的能匹配的点集的并,有\(|W|\leq|N(W)|\)
推论
两边点集为\(X,Y\),则二分图的最大匹配为\(|X|-max{\{|W|-|N(W)|\}}\),其中\(W\)是\(X\)的子集
欧拉公式
\(e^{ix}=cosx+isinx\)
阶(Order)
定义:
若\(a,p\)为正整数,且\(gcd(a,p)=1\),称满足\(a^r\equiv1(mod~p)\)的最小正整数\(r\)为\(a\)模\(p\)的阶,记为\(ord_p(a)\)
常用性质
1.若\(a,p\)为正整数,且\(gcd(a,p)=1\),\(r\)为\(a\)模\(p\)的阶,若有正整数\(m\)满足\(a^m\equiv1(mod~p)\),则\(r|m\)。
2.若\(a,p\)为正整数,且\(gcd(a,p)=1\),\(r\)为\(a\)模\(p\)的阶,则\(r|\phi(p)\)。
3.若\(a,p\)为正整数,且\(gcd(a,p)=1\),\(a^i\equiv a^j(mod~p)\)当且仅当\(i\equiv j(mod~ord_p(a))\).
原根(Primitive root)
定义:
若\(a,p\)为正整数,且\(gcd(a,p)=1\),称满足\(ord_p(a)=\phi(p)\)的叫做模\(p\)的一个原根。注意:不是任何\(p\)都存在原根。每个素数都存在原根。
常用性质:
1.当\(a\)为m的原根时,\(a^0,a^1,a^2,....,a^{m-1}\)构成了\(m\)的一个简化剩余类。
2.模m有原根的充要条件是\(m=2,4,p^n,2p^n\),其中\(p\)为奇素数,\(n\)为任意正整数
求解原根
我们知道了上述阶的性质2,要判断某数是不是模\(m\)的原根,可以验证是否存在m-1的一个约数a满足\(g^a\equiv 1(mod~m)\),如果有的话那么g的阶就不是\(m-1\),则\(g\)不是模\(m\)的原根。一般来说原根不会很大,从2开始枚举并按照上述方法判断就可以得到。
拉格朗日插值法
公式:
\(L(x)=\sum^{k}_{j=0}y_jp(x)\)
\(p_j(x)=\prod^k_{i=0,i\neq j}\frac{x-x_i}{x_j-x_i}\)
一个小性质
\(a\)与\(b\)互质,那么\((a+b)\)和\(a*b\)互质
l cm与gcd的一些性质
\(a={p_1} ^ {a_1} *{p_2} ^ {a_2} *..........*{p_n} ^ {a_n}\)
\(b={p_1} ^ {b_1} *{p_2} ^ {b_2} *..........*{p_n} ^ {b_n}\)
\(gcd(a,b)={p_1} ^{min(a_1,b_1)} * {p_2} ^ {min(a_2,b_2)} *..........*{p_n} ^ {min(a_n,b_n)}\)
\(lcm(a,b)={p_1} ^ {max(a_1,b_1)} *{p_2} ^ {max(a_2,b_2)} *..........*{p_n} ^ {max(a_n,b_n)}\)
斯特林公式
\(n!\approx\sqrt{2\pi n}(\frac{n}{e})^n\)
一些计算几何的公式
三角形外接圆半径\(R=\frac{a}{2sinA}\),由\(S=\frac{1}{2}bcsinA\),\(R=\frac{abc}{4S}\)
海伦公式\(S=\sqrt{p(p-a)(p-b)(p-c)},p=\frac{1}{2}(a+b+c)\)
莫比乌斯反演
\(F(n)=\sum\limits_{d|n}f(d)\)
\(f(n)=\sum\limits_{d|n}\mu(d)F(\lfloor\frac{n}{d}\rfloor)\)
\(F(n)=\sum\limits_{n|d}f(d)\)
\(f(n)=\sum\limits_{n|d}\mu{(\frac{d}{n})}F(d)\)
莫比乌斯函数的一些性质
\(\sum_{d|n}\mu(d)=[n=1]\)
\(\sum_{d|n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}\),这条性质将莫比乌斯函数和欧拉函数结合起来了
也就是狄利克雷卷积形式的\(\mu*id=\varphi~~~id(i)=i\)
杜教筛的套路式
假设要求的是\(S(n)=\sum\limits^n_{i=1}f(i)\)
构造一个积性函数\(g(x)\)
\(g(1)S(n)=\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)\)
二分图的一些定理
二分图的环只能是偶环
卡特兰数:
\(f(n)=\sum^{n-1}_{i=0}f(i)f(n-i-1) ,f(0)=f(1)=1\)
变形:
\(f(n)=C^n_{2n}-C^{n-1}_{2n}\)
卡特兰数的一些性质:
\(C_n=\frac{1}{n+1}C^n_{2n}=C^n_{2n}-C^{n-1}_{2n}\)
\(C_n=\frac{1}{n+1}\sum^n_{i=0}(C^i_n)^2\)
递推公式
\(C_{n+1}=\frac{2(2n+1)}{n+2}C_n,C_0=1\)
\(C_{n+1}=\sum^i_{i=0}C_iC_{n-i},C_0=1\)
关于勾股数
假设三个勾股数分别为\(x,y,z(z>x,y)\)
如果\(gcd(x,y,z)=1\)
那么先假设\(gcd(x,y)=g,g\neq1\)
那么说明\(x=k_1g,y=k_2g,z^2=(k_1^2+k_2^2)g^2,(k_1,k_2\in N^+)\)
那么提出\(g,z=\sqrt{k_1^2+k^2_1}g\)所以\(gcd(x,y,z)=g\)
所以要满足\(gcd(x,y,z)=1\)
必须要满足\(gcd(x,y)=1\),即\(x,y\)互质
对于满足这种类型(\(x,y\)互质)的勾股数
有一个通式:\(x=m^2-n^2,y=2mn,z=m^2+n^2,(gcd(m,n)=1且m,n必须一奇一偶,否则不满足互质条件,但依然是勾股数)\)
威尔逊定理
当且仅当\(p\)为素数时:\((p-1)!\equiv-1(mod p)\)
最长反链=最小链覆盖数
链是一个点的集合,这个集合中任意两个元素v、u,要么v能走到u,要么u能走到v。
反链是一个点的集合,这个集合中任意两点谁也不能走到谁。
最长反链是反链中最长的那个。
最小链覆盖。就是用最少的链,经过所有的点至少一次
最长反链长度 = 最小链覆盖数
建立两个n个点的点集X和Y,如果原图中存在一条边A->B,就在X中的A向Y中的B连边,跑最大匹配答案是ans,那么最长反链长度是n-ans
二分图中最小点覆盖等于最大匹配数
最小点覆盖:实质是个点集,点集里面的点能覆盖所有的边,最小点覆盖就是满足这个要求的点集中点数最小的那个
关于网络流跑二分图的复杂度
是\(n\sqrt{n}\)的,乱算复杂度算错结果导致不敢写的情况还是别再有了
柯西—施瓦茨不等式
对欧几里得空间有
\((\sum^n_{i=1}x_iy_i)^2\leqslant(\sum^n_{i=1}x_i^2)(\sum^n_{i=1}y_i^2)\)
对于平方可积的复值函数,有
\([\int^a_b f(x)g(x)dx]^2\leqslant \int^a_b f^2(x)dx\int^a_bg^2(x)dx\)
Betty定理
如果两个无理数\(a,b\)满足
\(\frac{1}{a}+\frac{1}{b}=1\)
那么对于两个集合A,B
\(A=\{ {\lfloor na \rfloor}\},B=\{ {\lfloor nb \rfloor}\},n\in{Z}\)
有两个结论:
\(A\bigcap B=\varnothing\)
\(A\bigcup B=N^+\)
类似整数划分的问题可以用该定理解决,如威佐夫博弈即可用此定理解决
算术基本定理
一个大于1的正整数\(N\),如果标准分解式为\(N=P^{a_1}_1P^{a_2}_2P^{a_3}_3\cdots P^{a_n}_n(表示质因数分解)\)
那么他的正因数个数为\((1+a_1)(1+a_2)\cdots (1+a_n)\)
他的全体正因数之和为\((1+p_1+p^2_1+\cdots+p_1^{a_1})(1+p_2+p^2_2+\cdots+p_2^{a_2})\cdots(1+p_n+p^2_n+\cdots+p_n^{a_n})\)
图上随机游走的定理
均等概率走或停,在无限步后停在某点的概率为,"该点的度数+1" 除以 "总度数+图上总节点数"
法里数列
欧拉定理
在一凸多面体中,顶点数-棱边数+面数=2
平方和
\(1^2+2^2+3^2+4^2\cdots=\frac{n(n+1)(2n+1)}{6}\)
立方和
\(1^3+2^3+3^3+4^3+\cdots=(1+2+3+4+\cdots)^2=(\frac{n(n+1)}{2})^2\)
皮克定理
皮克定理说明了其面积S和内部格点数目n、多边形边界上的格点数目s的关系:\(S=n+\frac{s}{2}-1\)
平面切分
n条直线能把平面切分成\(n(n+1)/2+1\)
n个平面能把空间分成\((n^3+5n+6)/6\)
笛卡尔定理
定义一个圆的曲率\(k = \pm\frac{1}{r}\),其中\(r\)是其半径。
若平面有两两相切,且有6个独立切点的四个圆,设其曲率为$k_1,k_2,k_3,k_4 $(若该圆与其他圆均外切,则曲率取正,否则取负)则其满足性质:
若平面上四个半径为\(r_1\)、\(r_2\)、\(r_3\)、\(r_4\)的圆两两相切于不同点,则其半径满足以下结论:
(1)若四圆两两外切,则
(2)若半径为\(r_1\)、\(r_2\)、\(r_3\)的圆内切于半径为r4的圆中,则
定理推广
笛卡尔定理在三维坐标系中也有类似的结论:若五个球的半径是\(r_i\)(1,2,...,5),满足任意一个球与其他四个球外切,则
圆的反演
1.一条不过反演中心的直线,反形是一个过反演中心的圆;(由反演的对称性)一个过反演中心的圆,反形是一条不过反演中心的直线。
2.一个不过反演中心的圆,反形也是一个不过反演中心的圆。反演中心是它们的位似中心,任一对反演点互为逆对应点
3.两个图形存在相切关系,那么反演后仍然满足相切关系。(特别地,如果以两圆切点作为反演中心,那么反演后的两条直线平行)
另外可以推出,相离的两圆反演(反演中心不在圆上)后仍然相离;两圆相切,若反演中心在某圆上,则为反形为相切的直线与圆
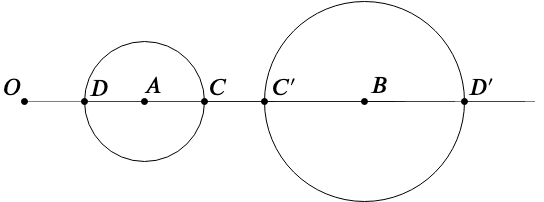
设O\((x_0,y_0)\)为反演点,以圆B与圆A互为反形
已知圆A半径为\(r_1\),圆心为\((x_1,y_1)\),反演半径为R,设圆B半径为\(r_2\),圆心为\((x_2,y_2)\)
根据反演定义有
\(|OD|*|OD'|=(|OA|-r_1)*(|OB|+r_2)=R^2\)
\(|OC|*|OC'|=(|OA|+r_1)*(|OB|-r_2)=R^2\)
消掉|OB|
解得\(r_2=\frac{1}{2}(\frac{R^2}{|OA|-r_1}-\frac{R^2}{|OA|+r_1})\)
\(x_2=x_0+\frac{|OB|}{|OA|}(x_1-x_0)\)
\(y_2=y_0+\frac{|OB|}{|OA|}(y_1-y_0)\)
其中\(|OB|=\frac{1}{2}(\frac{R^2}{|OA|-r_1}+\frac{R^2}{|OA|+r_1})\)
调和级数求和
可以选择分块预处理,当n特别大\(n>1e6\)的时候为\(f(n)=ln(n+1)+r\)
或者据说这个准一点\(h[n]=(log(n*1.0)+log(n+1.0)/2.0+1.0/(6.0*n*(n + 1))-1.0/(30.0*n*n*(n + 1)*(n+1))+r\)
\(r=0.57721566490153286060651209008240243104215933593992\)
\(r\)为欧拉常数


