Warshall算法求传递闭包及具体实现

传递闭包

在数学中，在集合 X 上的二元关系 R 的传递闭包是包含 R 的 X 上的最小的传递关系。

例如，如果 X 是(生或死)人的集合而 R 是关系“为父子”，则 R 的传递闭包是关系“x 是 y 的祖先”。再比如，如果 X 是空港的集合而关系 xRy 为“从空港 x 到空港 y 有直航”，则 R 的传递闭包是“可能经一次或多次航行从 x 飞到 y”。

Warshall算法

Warshall在1962年提出了一个求关系的传递闭包的有效算法。其具体过程如下，设在n个元素的有限集上关系R的关系矩阵为M：

（1）置新矩阵A=M;

（2）置k=1;

（3）对所有i如果A[i,k]=1，则对j=1..n执行：

A[i,j]←A[i,j]∨A[k,j];

（4）k增1;

（5）如果k≤n，则转到步骤（3），否则停止。

所得的矩阵A即为关系R的传递闭包t(R)的关系矩阵。

 要说跟floyd算法有什么关系的话...就是warshall求传递闭包他...他没有记录路径长度只是判断顶点之间是否直接或间接连通（个人理解）

代码实现：

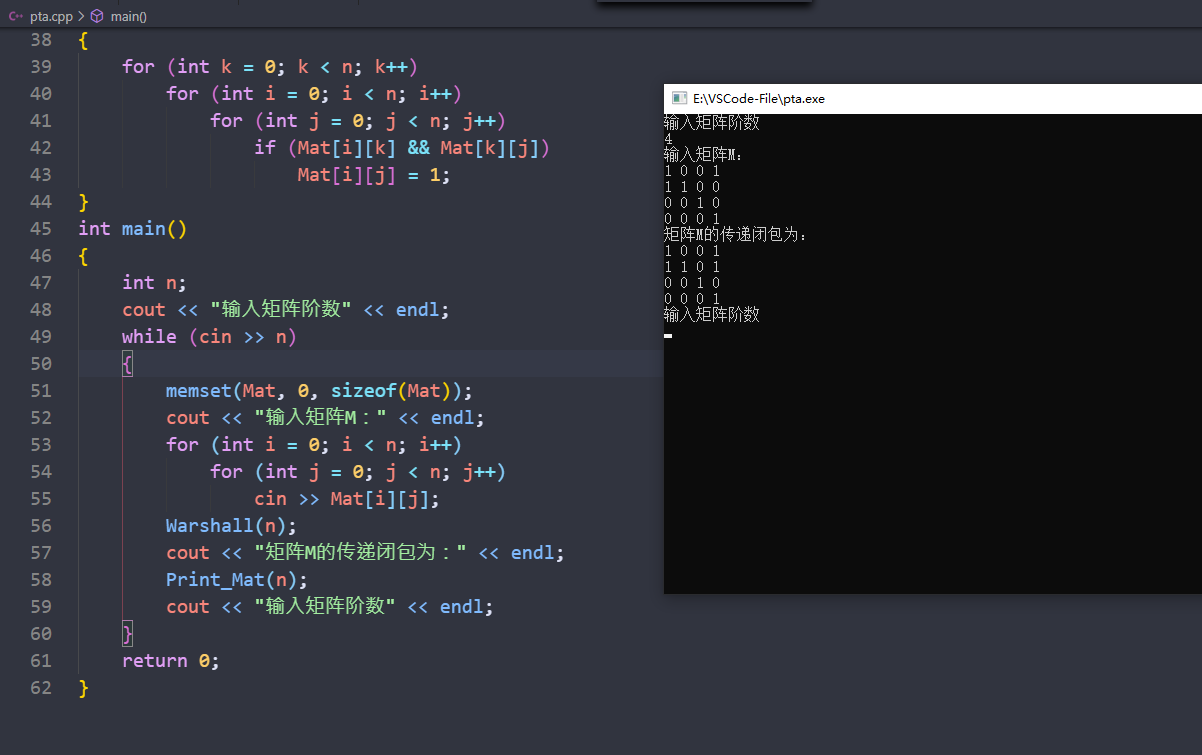
#include <bits/stdc++.h>
using namespace std;
/* freopen("k.in", "r", stdin);
freopen("k.out", "w", stdout); */
// clock_t c1 = clock();
// std::cerr << "Time:" << clock() - c1 <<"ms" << std::endl;
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#define de(a) cout << #a << " = " << a << endl
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define per(i, a, n) for (int i = n; i >= a; i--)
#define ls ((x) << 1)
#define rs ((x) << 1 | 1)
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<double, double> PDD;
typedef pair<ll, ll> PLL;
typedef vector<int, int> VII;
#define inf 0x3f3f3f3f
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll MAXN = 1e6 + 7;
const ll MAXM = 1e5 + 7;
const ll MOD = 1e9 + 7;
const double eps = 1e-6;
const double pi = acos(-1.0);
int Mat[20][20]; //
void Print_Mat(int n)
{
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            cout << Mat[i][j] << " ";
        cout << endl;
    }
    return;
}
void Warshall(int n)
{
    for (int k = 0; k < n; k++)
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                if (Mat[i][k] && Mat[k][j])
                    Mat[i][j] = 1;
}
int main()
{
    int n;
    cout << "输入矩阵阶数" << endl;
    while (cin >> n)
    {
        memset(Mat, 0, sizeof(Mat));
        cout << "输入矩阵M：" << endl;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                cin >> Mat[i][j];
        Warshall(n);
        cout << "矩阵M的传递闭包为：" << endl;
        Print_Mat(n);
        cout << "输入矩阵阶数" << endl;
    }
    return 0;
}