ACM YTU 1012 u Calculate e

u Calculate e

Problem Description

A simple mathematical formula for e is



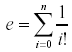
where n is allowed to go to infinity. This can actually yield very accurate approximations of e using relatively small values of n.

 

Output

Output the approximations of e generated by the above formula for the values of n from 0 to 9. The beginning of your output should appear similar to that shown below.

 

Sample Output

n e
- -----------
0 1
1 2
2 2.5
3 2.666666667
4 2.708333333

 

代码:

//  一道简单的递归题，需要0~9的阶乘，递归计算一下就行
//  输出的时候要注意保留9位小数，0也保留

#include <iostream>
#include<stdio.h>
using namespace std;
int fun[10];
double a[1000] = {0.0};
int g(int x)//递归求0--9的阶乘
{
    int z;
    if(x <= 1 )
        z = 1;
    else
        z = g(x-1)*x;
    return z;
}
void f()
{
    a[0] = 1;
    a[1] = 2;
    for(int i = 2;i<10;i++)
    {
        a[i] = a[i-1]+(1/(double)g(i));
    }
}

int main()
{
    f();
    cout<<"n e"<<endl;
    cout<<"- -----------"<<endl;
    cout<<0<<" "<<a[0]<<endl;
    cout<<1<<" "<<a[1]<<endl;
    cout<<2<<" "<<a[2]<<endl;
    for(int i = 3;i<10;i++)
    {
        printf("%d %11.9f\n",i,a[i]);
        //cout.precision(10);
        //cout<<i<<" "<<a[i]<<endl;
        // C++的cout.precision(x);不保留0，要注意
    }

        //cout<<f(n)<<endl;

    return 0;
}