hdu Train Problem I(栈的简单应用)

Problem Description

As the new term comes, the Ignatius Train Station is very busy nowadays. A lot of student want to get back to school by train(because the trains in the Ignatius Train Station is the fastest all over the world ^v^). But here comes a problem, there is only one railway where all the trains stop. So all the trains come in from one side and get out from the other side. For this problem, if train A gets into the railway first, and then train B gets into the railway before train A leaves, train A can't leave until train B leaves. The pictures below figure out the problem. Now the problem for you is, there are at most 9 trains in the station, all the trains has an ID(numbered from 1 to n), the trains get into the railway in an order O1, your task is to determine whether the trains can get out in an order O2.

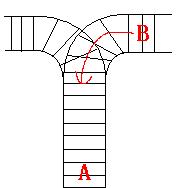
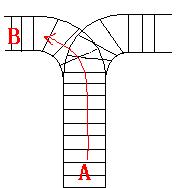
Input

The input contains several test cases. Each test case consists of an integer, the number of trains, and two strings, the order of the trains come in:O1, and the order of the trains leave:O2. The input is terminated by the end of file. More details in the Sample Input.

Output

The output contains a string "No." if you can't exchange O2 to O1, or you should output a line contains "Yes.", and then output your way in exchanging the order(you should output "in" for a train getting into the railway, and "out" for a train getting out of the railway). Print a line contains "FINISH" after each test case. More details in the Sample Output.

Sample Input

3 123 321
3 123 312

Sample Output

Yes.
in
in
in
out
out
out
FINISH
No.
FINISH

Hint

For the first Sample Input, we let train 1 get in, then train 2 and train 3.
So now train 3 is at the top of the railway, so train 3 can leave first, then train 2 and train 1.
In the second Sample input, we should let train 3 leave first, so we have to let train 1 get in, then train 2 and train 3.
Now we can let train 3 leave.
But after that we can't let train 1 leave before train 2, because train 2 is at the top of the railway at the moment.
So we output "No.".

思路:

栈的简单应用，输入为一个数n 和两个长度为 n 的字符串，第一个为入站序列 O1，第二个为出站序列 O2，我们只需要判断根据入站序列是否能得到出站序列，如果能救输入可能的出站序列，否则输出NO。

可以知道如果两个序列吻合，进出站顺序唯一，所以就在进站的同时判断能否出站，能则出站，否则继续进站，遍历。。

 代码:

#include<iostream>
#include<string.h>
#include<stack>
using namespace std;
int main()
{
    int n, i, j, k, flag[50];
    char s1[15], s2[15];
    stack <char> s;
    while(cin>>n>>s1>>s2)
    {
        	while(!s.empty())   //清空栈
            s.pop();
        memset(flag,-1,sizeof(flag));
        j = k = 0;
        for(i = 0; i < n; i++)
        {
            s.push(s1[i]);   //  进栈
            flag[k++] = 1;//   进栈为1，in
            while(!s.empty() && s.top() == s2[j])  //出栈：栈为空或者栈顶元素与出
////站指针所在位置相等
            {
                flag[k++] = 0;//出栈为0 out
                s.pop();
                j++;
            }
        }
        if(j == n)  //如果 j = n 说明出栈完毕。
        {
            cout<<"Yes."<<endl;
            for(i = 0; i < k; i++)
            {
                if(flag[i])
                    cout<<"in"<<endl;
                else
                    cout<<"out"<<endl;
            }
        }
        else
            cout<<"No."<<endl;
        cout<<"FINISH"<<endl;
    }
    return 0;
}