Paper - 2014 - A double layer method for constructing signed distance fields from triangle meshes

Paper - 2014 - A double layer method for constructing signed distance fields from triangle meshes

Wu, Y., Man, J., & Xie, Z. (2014). A double layer method for constructing signed distance fields from triangle meshes. Graphical Models, 76(4), 214–223. https://doi.org/10.1016/j.gmod.2014.04.011

我们算法的主要贡献如下：

• 内表面，外表面距离场分别考虑，网格转换成点云，避免三角形相关的求解过程；
• 将内外的距离场合并为一个，并且能够快速的确定符号；
• 算法很容易进行并行化；

3. the proposed algorithm

网格需要满足：

• 三角形之间共享顶点或边，否则是相离的；
• 每条边仅和两个三角形相邻；
• 和顶点相关联的三角形，刚好在周围形成一圈；

对于流形的网格我们定义internal和external layer如下：

其中\(\delta\)是小正数。如果距离场\(D_I(D_E)\)是已知的，那么可以计算得到M的符号距离场\(\phi\)。如上图所示，针对位于网格内部的点，\(D_I(p) \le D_E(p)\), 有由于\(|\phi|+\delta = D_E\)，位于内部的符号距离场为负数，那么针对M内部的点，我们得到\(\phi(p) = -(D_E(p) - \delta)\)。

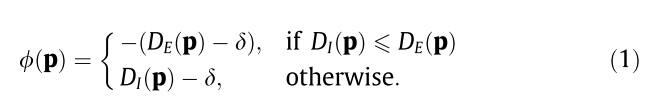
那么整个算法可以分解成如下几个步骤：

• 初始化所有3D grid场，\(D_I,D_E,\phi\). 初始化成相同维度，较大的值如10e8即可。
• 计算internal和external distance field
• 生成最后的距离场；

3.2 Compute internal and external distance field From

为了计算internal（external） distance field。首先需要计算internal（external）点集。针对M的每个三角形可以计算得到它的法向量和面积，如下：

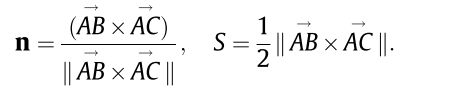
那么内层外层点集的计算如下：

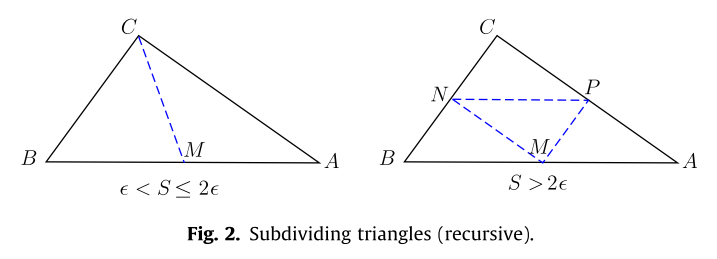
接下来的问题是如何从三角形中采样合适的点。这里给出的策略是，如果三角形的面积足够小（如，\(S < \epsilon\)），那么直接选择三角形的重心。如果三角形很大，那么需要进行细分，然后选择小三角形的重心。具体细分如下图所示：

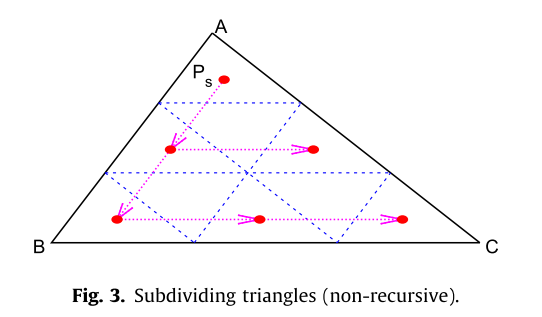
并提供了非递归细分的算法：

该实现的采样过程如下所示：

当计算得到内层点和外层点之后，假设我们先计算内层的distance field。我们找到\(p\)，然后更新该点(2K+1)x(2K+1)x(2K+1)领域内grid的distance filed。选择合适的领域范围。

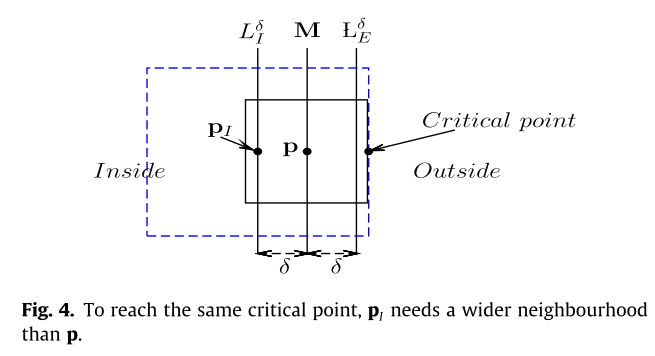
3.3 Generate the signed distance field

可以通过公式1对距离场进行计算。但是，它的正负性可能由于浮点计算误差出现异常，因此进行改进如下：

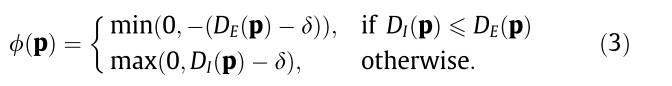
当M领域的符号都确定了之后，对整个场进行遍历，可以对网格内部的数据结合领域的符号信息确定它的符号。最后得到的结果，在超过M领域范围的数值并不能准确的表示距离场。如有必要可以通过其他的distance transform方法获取完整的距离场。

4. Analysis and optimizations

这节内容，对误差进行了分析。并讨论了一些优化措施。误差范围如下：

同时存在符号误差。

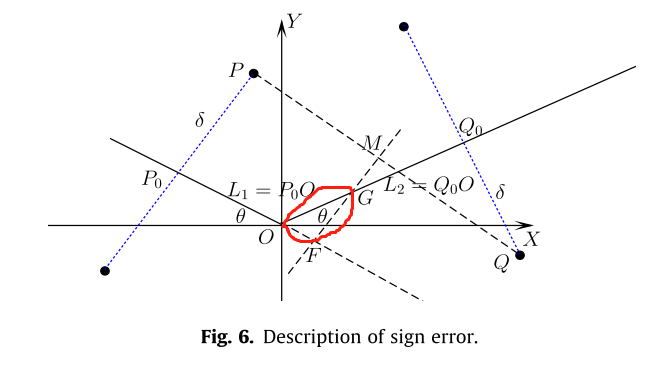
上述三角形区域中的点的符号会发生误判。由于of区域比较小，这个误差并不会扩张。

4.2 optimization

先存储距离的平方，而不是执行开根号。

5 results

一些测试结果如下：

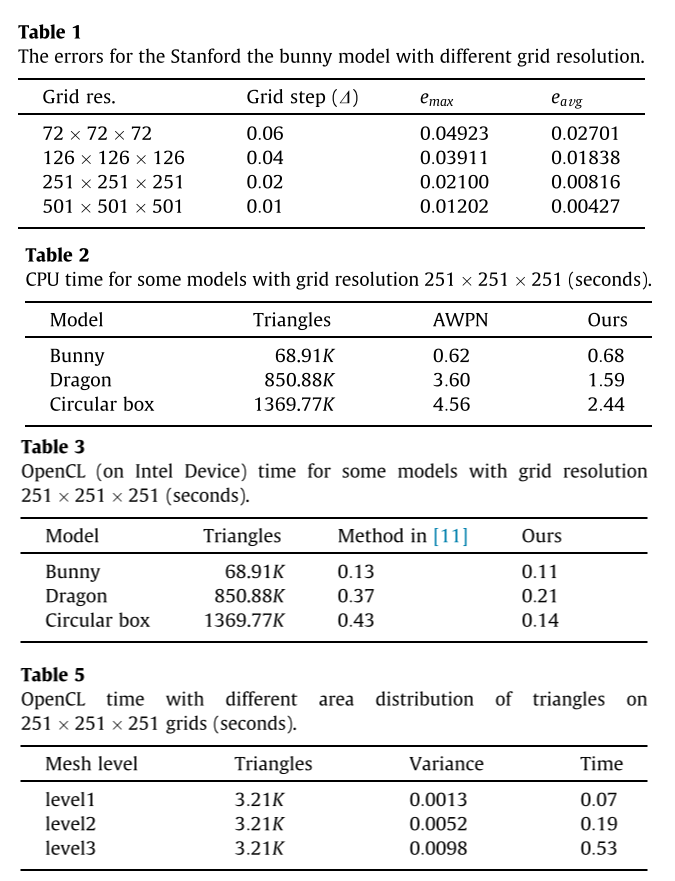
ref:

S. Mauch, A Fast Algorithm for Computing the Closest Point and Distance Transform, 2000. <http://www.acm.caltech.edu/seanm/ software/cpt/cpt.pdf>.

利用GPU进行加速。

A. Sud, N. Govindaraju, R. Gayle, E. Andersen, D. Manocha, Surface distance maps, in: Proceedings of Graphics Interface 2007, ACM, 2007,

A. Sud, N. Govindaraju, R. Gayle, D. Manocha, Interactive 3D distance field computation using linear factorization, in: Proceedings of the 2006 Symposium on Interactive 3D Graphics and Games, ACM, 2006, pp.

G. Rong, T.-S. Tan, Jump flooding in GPU with applications to Voronoi diagram and distance transform, in: Proceedings of the 2006 Symposium on Interactive 3D Graphics and Games, ACM, 2006, pp. 109–116.

C. Sigg, R. Peikert, M. Gross, Signed distance transform using graphics hardware, in: Visualization, 2003. VIS 2003, IEEE, 2003, pp.