source impl - 网格差异可视化

source impl - 网格差异可视化

[[paper-1998-metro-measuring-error-on-simplified-surfaces]] 介绍了网格近似误差的计算。这里需要完成的是输入两个网格（通常是基准网格和变化后的网格，如精简，重新生成，细分等）。计算变化后的网格上的所有的顶点，相对于基准网格的距离，然后对变化后的网格进行绘制，并将距离用伪彩的颜色进行显示。

此处借助八叉树的空间划分结构。划分的对象为三角网格的顶点，八叉树的实现参考：brandonpelfrey/SimpleOctree: A simple octree with good commenting for learning how octrees work. (github.com)

空间划分结束后，遍历变化后的网格的所有顶点v_i，在构建的八叉树中查找对应的box。从该box中取出含有的基准网格的顶点v_j。然后计算v_i和v_j相邻三角形的最短距离，即为最后计算得到的结果。伪代码如下：

# input: triMesh, triMeshBase
# output: triMesh with min distance vertex property
octree = constructOctree(triMeshBase)
for vertex in triMesh:
	leaf = octree.findLeaf(vertex)
	for vertexBase in leaf:
		for triangle around vertexBase:
			vertex.minDis = min(vertex.minDis, distance(vertex, triangle))

openmesh 顶点划分的八叉树

如果直接利用链接中的实现，对点云进行八叉树划分，那么点对应的面，边的拓扑信息就会丢失，因此，这里对原来的实现进行了更改，使得每个叶子节点存储openmesh的顶点handle，这样就很方便获取拓扑信息。同时对八叉树的深度进行了限制。

利用八叉树，可以找到某个点最近的顶点，然后获取该顶点周围的三角形，进一步计算顶点和三角形之间的距离，此处可以参考：GeometricTools/DistPointTriangle.h at master · davideberly/GeometricTools (github.com) 。

八叉树的主要代码如下：

// ref: https://github.com/brandonpelfrey/SimpleOctree
// https://www.cnblogs.com/Glucklichste/p/11505743.html

#ifndef OPENMESH_Octree_H
#define OPENMESH_Octree_H

#include <cstddef>
#include <vector>

#include "openmesh_typedef.h"
#include "openmesh_utils.h"

/**!
 * Octree data struct used for openmesh datastruct
 */
class OpenMeshOctree {
    /*
        Children follow a predictable pattern to make accesses simple.
        Here, - means less than 'origin' in that dimension, + means greater than.
        child:	0 1 2 3 4 5 6 7
        x:      - - - - + + + +
        y:      - - + + - - + +
        z:      - + - + - + - +
     */
public:
    OpenMeshOctree(const TriMesh& triMesh, const TriMesh::Point& origin, const TriMesh::Point& halfDimension, unsigned int currentDepth)
    : triMesh_(triMesh), origin_(origin), halfDimension_(halfDimension), currentDepth_(currentDepth)
    {
        // Initially, there are no children
        for(int i=0; i<8; ++i) 
            children_[i] = nullptr;
    }

    OpenMeshOctree(const OpenMeshOctree& copy) = delete;

    ~OpenMeshOctree() 
    {
        // Recursively destroy octants
        for (int i = 0; i < 8; ++i)
        {
            if (children_[i])
                delete children_[i];
        }
    }

    void Insert(const TriMesh::VertexHandle& vh) {
        if (currentDepth_ == 0)  // Reach the max depth
        {
            data_.insert(vh);
            return;
        }
        else if (!hasChild_ && data_.empty()) // the current node has no data and has no child
        {
            data_.insert(vh);
            return;
        }
        else if (!hasChild_ && !data_.empty()) // the current node has no child and has data
        {
            // We're at a leaf, but there's already something here
            // We will split this node so that it has 8 child octants
            // and then insert the old data that was here, along with 
            // this new data point
            std::set<TriMesh::VertexHandle> oldData;
            oldData.swap(data_);

            assert(oldData.size() == 1);

            // only create used child
            int idxChild0 = GetOctantContainingPoint(*oldData.begin());
            int idxChild1 = GetOctantContainingPoint(vh);
            int idxChild[] = { idxChild0, idxChild1 };
            int idxChildCount = idxChild0 == idxChild1 ? 1 : 2;
            for (int i = 0; i < idxChildCount; ++i)
            {
                if (children_[idxChild[i]] == nullptr)
                {
                    TriMesh::Point newOrigin = origin_;
                    newOrigin[0] += halfDimension_[0] * (idxChild[i] & 4 ? .5f : -.5f);
                    newOrigin[1] += halfDimension_[1] * (idxChild[i] & 2 ? .5f : -.5f);
                    newOrigin[2] += halfDimension_[2] * (idxChild[i] & 1 ? .5f : -.5f);
                    children_[idxChild[i]] = new OpenMeshOctree(triMesh_, newOrigin, halfDimension_ * .5f, currentDepth_ - 1);
                }
            }

            // Re-insert the old point, and insert this new point
            // (We wouldn't need to insert from the root, because we already
            // know it's guaranteed to be in this section of the tree)
            children_[idxChild0]->Insert(*oldData.begin());
            children_[idxChild1]->Insert(vh);
            hasChild_ = true;
        }
        else
        {
            // We are at an interior node. Insert recursively into the 
            // appropriate child octant
            int octant = GetOctantContainingPoint(vh);
            if (children_[octant] == nullptr)
            {
                TriMesh::Point newOrigin = origin_;
                newOrigin[0] += halfDimension_[0] * (octant & 4 ? .5f : -.5f);
                newOrigin[1] += halfDimension_[1] * (octant & 2 ? .5f : -.5f);
                newOrigin[2] += halfDimension_[2] * (octant & 1 ? .5f : -.5f);
                children_[octant] = new OpenMeshOctree(triMesh_, newOrigin, halfDimension_ * .5f, currentDepth_ - 1);
            }
            children_[octant]->Insert(vh);
        }
    }

    // The PointType must support
    // pt[0], pt[1], pt[2] to access the coordinate value
    template <typename PointType>
    void GetNodeContainPoint(const PointType& pt, OpenMeshOctree*& result)
    {
        // Compute the min/max corners of this child octant
        auto cmax = origin_ + halfDimension_;
        auto cmin = origin_ - halfDimension_;

        // If the query rectangle is outside the child's bounding box, 
        // then continue
        if (cmax[0] < pt[0] || cmax[1] < pt[1] || cmax[2] < pt[2]) return;
        if (cmin[0] > pt[0] || cmin[1] > pt[1] || cmin[2] > pt[2]) return;

        result = this;

        bool isLeafNode = !hasChild_ || currentDepth_ == 0;
        if (!isLeafNode)
        {
            for (int i = 0; i < 8; ++i) {
                if (children_[i] == nullptr) continue;

                // At this point, we've determined that this child is containing the pt 
                children_[i]->GetNodeContainPoint(pt, result);
            }
        }
    }

    void GetDataInCurrentNode(std::set<TriMesh::VertexHandle>& data)
    {
        bool isLeafNode = !hasChild_ || currentDepth_ == 0;

        if (isLeafNode)
        {
            data.insert(data_.begin(), data_.end());
        }
        else
        {
            for (int i = 0; i < 8; ++i)
            {
                if (children_[i] == nullptr) continue;
                children_[i]->GetDataInCurrentNode(data);
            }
        }
    }

private:
    // Determine which octant of the tree would contain 'point'
    int GetOctantContainingPoint(const TriMesh::VertexHandle& vh) const {
        const TriMesh::Point& point = triMesh_.point(vh);
        int oct = 0;
        if (point[0] >= origin_[0]) oct |= 4;
        if (point[1] >= origin_[1]) oct |= 2;
        if (point[2] >= origin_[2]) oct |= 1;
        return oct;
    }

    const TriMesh& triMesh_;

    // Physical position/size. This implicitly defines the bounding 
    // box of this node
    TriMesh::Point origin_;         //! The physical center of this node
    TriMesh::Point halfDimension_;  //! Half the width/height/depth of this node

    // The tree has up to eight children and can additionally store
    // a point, though in many applications only, the leaves will store data.
    OpenMeshOctree* children_[8]; //! Pointers to child octants
    std::set<TriMesh::VertexHandle> data_;   //! Data point to be stored at a node

    unsigned int currentDepth_ = 0; // The depth of root is max, the depth of leaf node is 0 or all child is null
    bool hasChild_ = false;
};

/// \brief Create octree data struct from openmesh trimesh 
/// \param[in] trimesh input triangle mesh
/// \param[in] maxDepth max depth of octree, the depth is from 16(root) to 0
OpenMeshOctree* CreateOpenMeshOctree(const TriMesh& trimesh, unsigned int maxDepth = 16)
{
    TriMesh::Point low, high;
    GetTriMeshBoundingBox(trimesh, low, high);

    TriMesh::Point center = (low + high) * 0.5;
    TriMesh::Point halfDimension = (high - low) * 0.5;

    OpenMeshOctree* root = new OpenMeshOctree(trimesh, center, halfDimension, maxDepth);
    for (auto vh : trimesh.vertices())
    {
        root->Insert(vh);
    }

    return root;
}

OpenMeshOctree* CreateOpenMeshOctree(const TriMesh& trimesh, const TriMesh::Point& low, const TriMesh::Point& high, unsigned int maxDepth = 16)
{
    TriMesh::Point center = (low + high) * 0.5;
    TriMesh::Point halfDimension = (high - low) * 0.5;

    OpenMeshOctree* root = new OpenMeshOctree(trimesh, center, halfDimension, maxDepth);
    for (auto vh : trimesh.vertices())
    {
        root->Insert(vh);
    }

    return root;
}

#endif

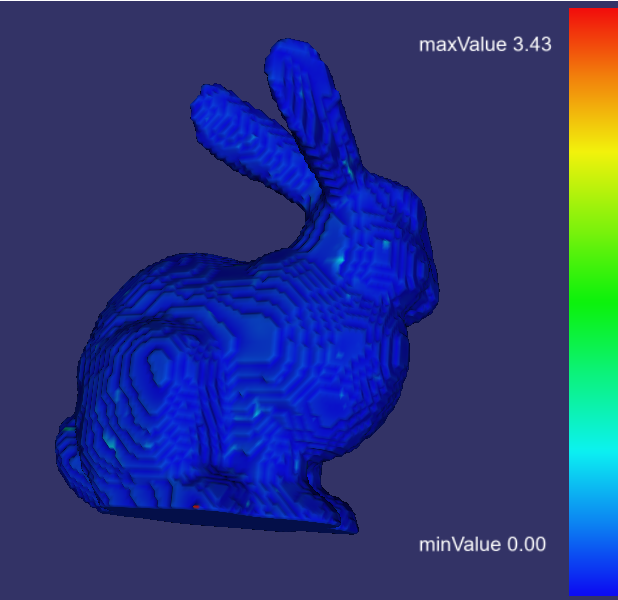
OSG可视化结果