games101 - 1 - Rasterization

games101 - 1 - Rasterization

GAMES101:现代计算机图形学入门 – 计算机图形学与混合现实研讨会 (games-cn.org)

涉及到的课程有：Lecture 5 ~ Lecture 6

• 简介
• 采样
• 采样引入的问题
• 反走样原理及实现

简介

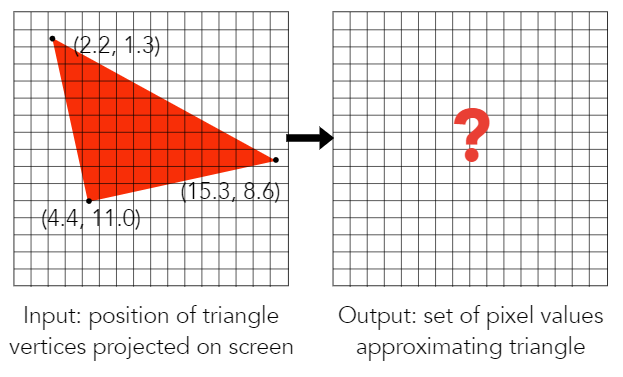
光栅化的过程主要是为了描述如何利用像素值去表示几何（如，图中的三角形）。

光栅化的实现，最常见的方法是采样。而采样会引入一些问题，如要借助一些技术解决这些问题。

采样

什么是采样：对一个连续对象（可以是连续函数，绘制的几何对象），离散化的过程就是采样。比如：

for (int x = 0; x < xmax; ++x)
	output[x] = f(x);

在图形学中，常见的采样对象可以是：时域，面积，方向，体积（time，area，direction，volume）等。对于三角形的光栅化，可以考虑成在面积上进行采样，对每个像素点，判断是不是位于三角形内部，如果是则进行填色，否则略过，如下图：

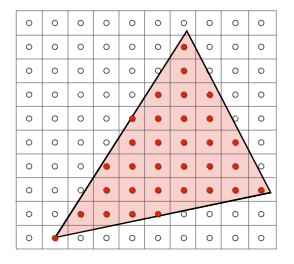
伪代码如下：

for (int x = 0; x < xmax; ++x)
    for (int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri, x+0.5, y+0.5);

由于此处采样的是像素点的中心，因此有0.5的偏移，如下图所示：

关于软光栅化可以参见：软光栅-uraster代码阅读（入门极品） - grassofsky - 博客园 (cnblogs.com)

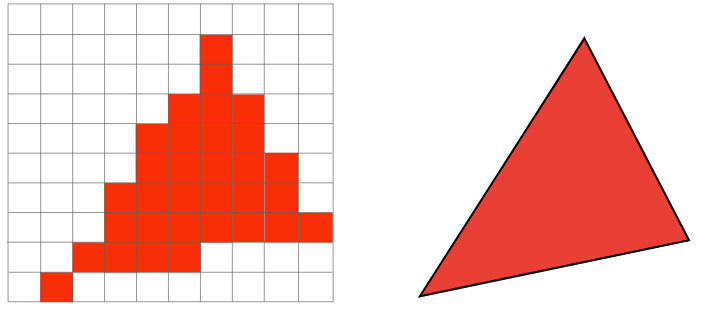
最后给出采样后和原始三角形的对比图：

采样引入的问题（走样，Aliasing）

上一节中我们可以看到采样后的结果，也可以发现一个很明显的问题：存在严重的锯齿，边界过度不够自然。除了锯齿，采样还会引起别的什么问题呢？

摩尔纹：

车轮错觉:

还有别的很多问题【TODO】

这些问题的背后的原因是什么呢？

信号改变的太快（高频信号），但是采样的太慢（低频采样）

反走样Anti-Aliasing原理及实现

反走样的简单实现：先平滑（滤波）后采样

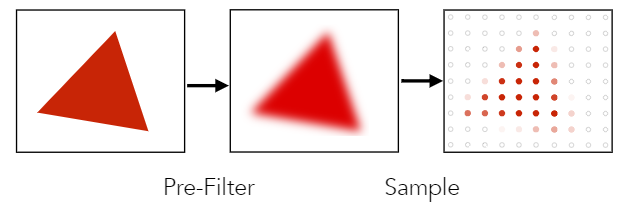
此时生成的结果的边界不再是名下的纯色，而是渐变的过度色，这样视觉上，锯齿的现象就不明显了。具体效果：

这里有一点需要注意的是，需要对原始连续图像进行平滑，然后再进行采样，不能先进行采样，再进行平滑。先采样，导致锯齿已经存在了，再进行平滑，只是会将锯齿变糊，并不能去掉锯齿，如下对比图所示：

那么此处会产生以下问题：

• 为什么欠采样会引起锯齿？
• 为什么先平滑（滤波）再采样可以抗锯齿？

走样背后的原理

先来看下傅里叶变换：深入浅出的讲解傅里叶变换（真正的通俗易懂） - h2z - 博客园 (cnblogs.com)

接着看些欠采样会有什么问题：

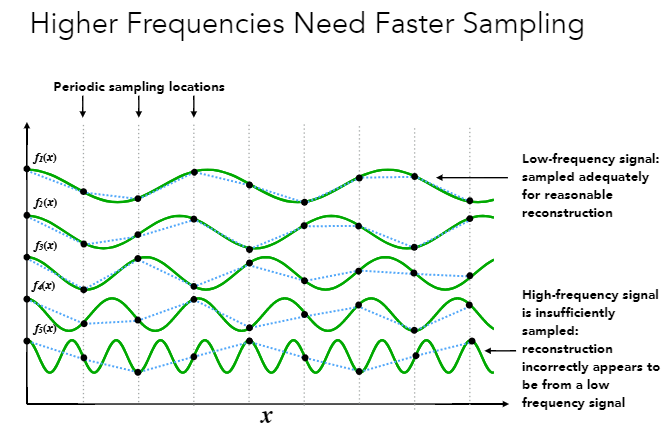
从上图可以知道，对于高频信号，如果采样频率不够，那么采样得到的结果和原始结果会相差十万八千里。

滤波的作用是剔除掉特定频率内容

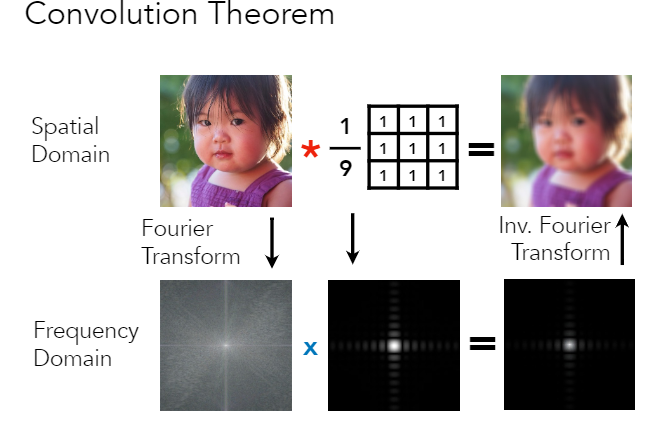
滤波 = 卷积 = 平均

分为时域卷积定理和频域卷积定理，时域卷积定理即时域内的卷积对应频域内的乘积；频域卷积定理即频域内的卷积对应时域内的乘积，两者具有对偶关系。具体公式如下：

\[F[f_1(t) * f_2(t) ] = F_1(\omega) \bullet F_2(\omega) \\ F[f_1(t) \bullet f_2(t)] = \frac{1}{2\pi}F_1(\omega)*F_2(\omega) \]

其中\(*\)表示卷积。示意图如下：

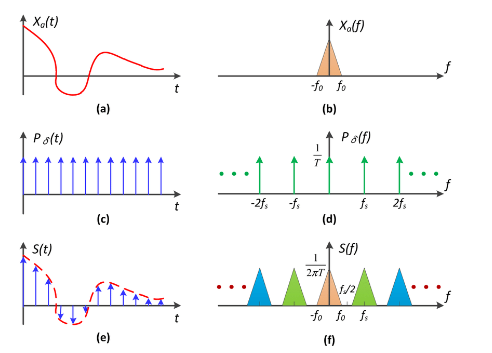
时域上的采样 = 频域上的卷积 = 重复频域中的内容

走样 = 频域中内容出现混叠

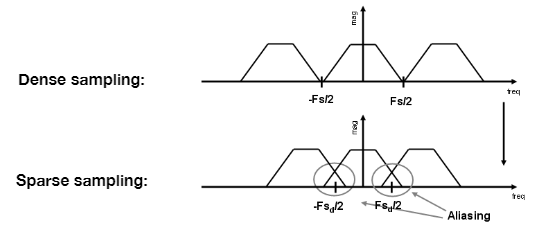
减少走样背后的原理

那么如何实现反走样呢？通常有两种途径：

第一种途径是增加采样频率：

• 本质是增加频域内重复对象之间的距离；
• 通常可以借助更高分辨率的显示器，探测器，framebuffer等实现；

这种方法通常开销大，以及需要更高的分辨率。

第二种途径是：利用反走样技术。

• 使得频域中的对象在重复之前，进行裁剪；比如，在采样之前过滤高频的部分，如下图所示：

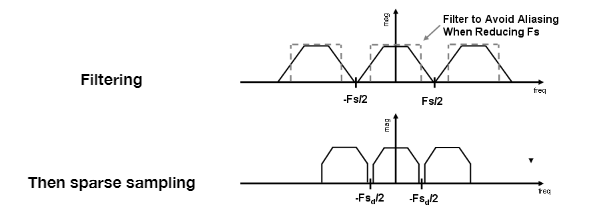
反走样 = Limiting，then repeating

反走样的实现

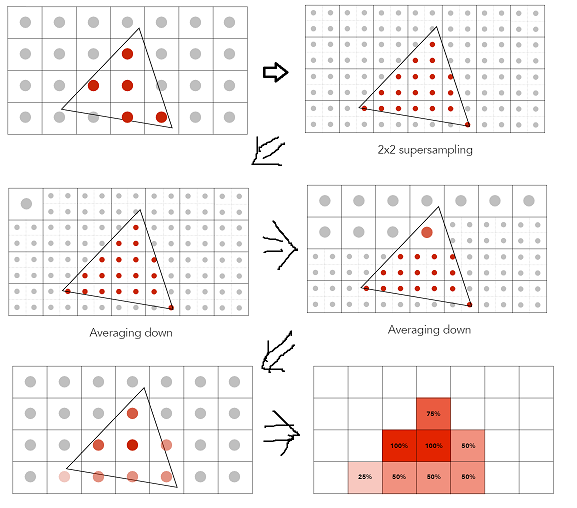
Antialiasing By Supersampling (MSAA)

原理实现如下图所示：

其他的反走样实现【todo】

• FXAA (Fast Approximate AA)
• TAA (Temporal AA)
• DLSS (Deep Learning Super Sampling)