mysql索引B+树

注：数据结构与算法，这门学科从诞生到现在，自始至终都让人难以理解，但国外有一个比较厉害的程序员，为了帮助他人更好的理解数据结构，自己搭建了一个数据结构的动画演示平台，里面提供了非常多丰富的数据结构类型，我们在其中能以动画的形式观测数据结构的变化。

索引存储数据结构

1、哈希表

哈希表是一种以键-值（key-value）存储数据的结构，我们只要输入待查找的值即key，就可以找到其对应的值即Value。哈希的思路很简单，把值放在数组里，用一个哈希函数把key换算成一个确定的位置，然后把value放在数组的这个位置。

不可避免地，多个key值经过哈希函数的换算，会出现同一个值的情况。处理这种情况的一种方法是，拉出一个链表。

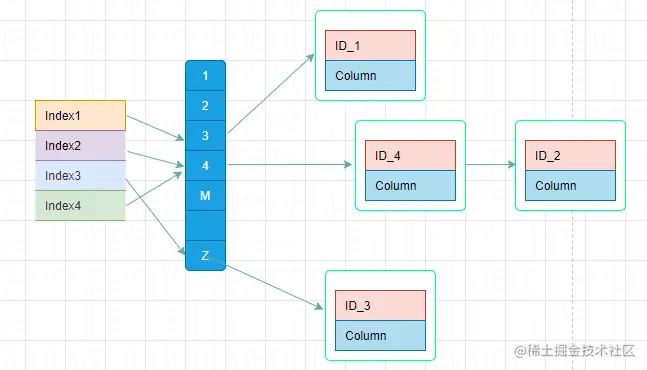
所以，需要注意，哈希表后的链表并不是有序的，区间查询的话需要扫描链表，所以哈希表这种结构适用于只有等值查询的场景，比如Memcached及其他一些NoSQL引擎。

2、有序数组

另外一个大家比较熟悉的数组结构，有序数组在等值查询和范围查询场景中的性能都非常优秀。

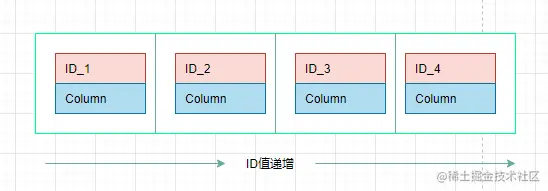
如果仅仅看查询效率，有序数组是非常棒的数据结构。但是，在需要更新数据的时候就麻烦了，你往中间插入一个记录就必须得挪动后面所有的记录，成本太高。

所以，有序数组索引只适用于静态存储引擎，比如你要保存的是2017年某个城市的所有人口信息，这类不会再修改的数据。

这两种都不是最主要的索引，常见的索引使用的数据结构是树结构，树是数据结构里相对复杂一些的数据结构，我们来一步步认识索引的树结构。

3、二分查找

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

查找方法：首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

上面提到的有序数组的等值查询和比较查询效率非常高，但是更新数据存在问题。

为了支持频繁的修改，比如插入数据，我们需要采用链表。链表的话，如果是单链表，它的查找效率还是不够高。

所以，有没有可以使用二分查找的链表呢?

为了解决这个问题，BST(Binary Search Tree)也就是我们所说的二叉查找树诞生了。

4、二叉查找树

二叉树具有以下性质：左子树的键值小于根的键值，右子树的键值大于根的键值。

如下图所示就是一棵二叉查找树，

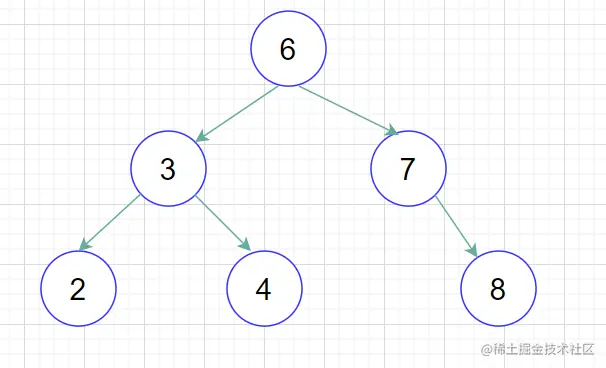
在这种比较平衡的状态下查找时间复杂度是O(log(n))。

但是二叉查找树存在一个问题：在某些极端情况下会退化成链表。

同样是2,3,4,6,7,8这六个数字，如果我们插入的数据刚好是有序的，那它就变成这样👇

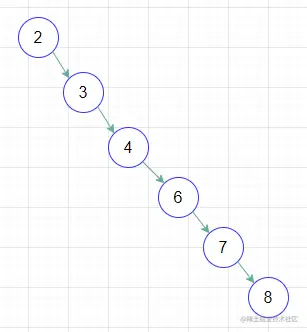
这个时候，二叉查找树查找的时间复杂度就和链表一样，是O(n)。

造成它“叉劈”的原因是什么呢? 因为左右子树深度差太大，这棵树的左子树根本没有节点——也就是它不够平衡。

所以，我们有没有左右子树深度相差不是那么大，更加平衡的树呢? ——那就就是平衡二叉树，叫做 Balanced binary search trees，或者 AVL 树。

5、AVL 树

AVL Trees (Balanced binary search trees) 平衡二叉树的定义:左右子树深度差绝对值不能超过 1。

例如左子树的深度是 2，右子树的深度只能是 1 或者 3。 这个时候我们再按顺序插入 2,3,4,6,7,8，就不会“叉劈”👇

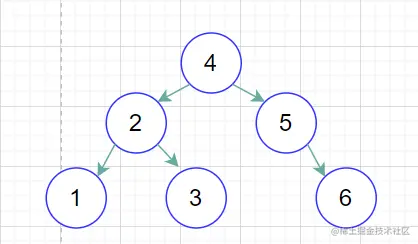
AVL树的平衡是怎么做到的呢？主要用到了两个操作左旋、右旋。

• 插入 1、2、3。

  当我们插入了 1、2 之后，如果按照二叉查找树的定义，3 肯定是要在 2 的右边的，这个时候根节点 1 的右节点深度会变成 2，但是左节点的深度是 0，因为它没有子节点，所以就会违反平衡二叉树的定义。

  那应该怎么办呢?因为它是右节点下面接一个右节点，右–右型，所以这个时候我们要把 2 提上去，这个操作叫做左旋。

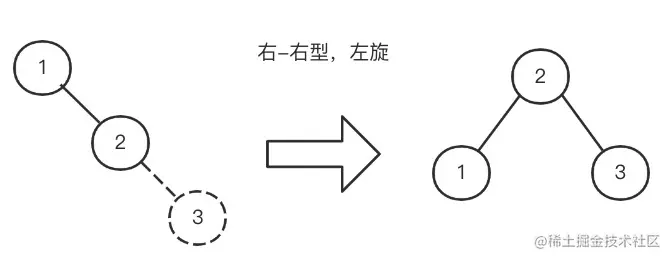
• 同样的，如果我们插入3、2、1，这个时候会变成左左型，就会发生右旋操作，把 2提上去。

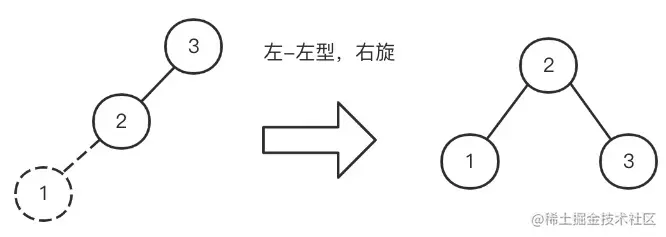
既然平衡二叉树能保持平衡，不会退化，那么我们用平衡二叉树存储索引可以吗？——可以的。

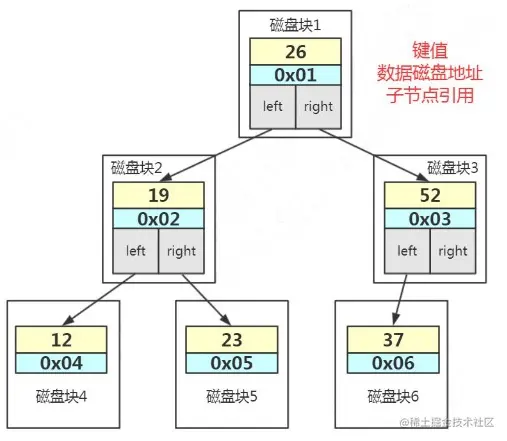
当我们用树的结构来存储索引的时候，访问一个节点就要跟磁盘之间发生一次 IO。 InnoDB 操作磁盘的最小的单位是一页(或者叫一个磁盘块)。与主存不同，磁盘I/O存在机械运动耗费，因此磁盘I/O的时间消耗是巨大的。

所以如果每个节点存储的数据太少，从索引中找到我们需要的数据，就要访问更多的节点，意味着跟磁盘交互次数就会过多。

那么解决方案是什么？

• 让每个节点存储更多的数据。

• 让节点上有更多的关键字。

节点上的关键字的数量越多，我们的指针数也越多，也就是意味着可以有更多的分叉(我们把它叫做“路数”)。

因为分叉数越多，树的深度就会减少(根节点是 0)。 这样，树就从瘦高变成了矮胖。

这个时候，我们的树就不再是二叉了，而是多叉，或者叫做多路。

6、多路平衡查找树（B-Tree）

接下来看一下多路平衡查找树，也就是B树。

B树是一种多叉平衡查找树，如下图主要特点：

• B树的节点中存储着多个元素，每个内节点有多个分叉。
• 节点中的元素包含键值和数据，节点中的键值从大到小排列。也就是说，在所有的节点都储存数据。
• 父节点当中的元素不会出现在子节点中。
• 所有的叶子结点都位于同一层，叶节点具有相同的深度，叶节点之间没有指针连接。

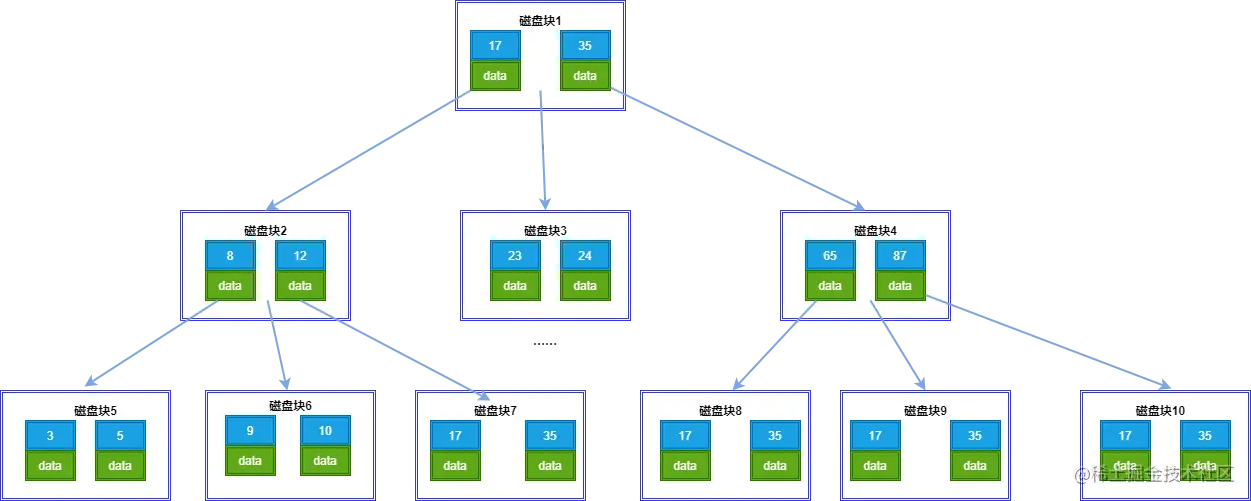
以上图为例，我们来简单看几个查询：

• 如果查找key<17，就走左边子节点；
• 如果查找17<key<35，就走中间子节点；
• 如果查找key>35，就走右边子节点；
• 如果查找key=17，直接命中；
• 如果查找key=35，直接命中；

B树看起来很完美，到这就结束了吗？并没有。

• B树不支持范围查询的快速查找，你想想这么一个情况如果我们想要查找10和35之间的数据，查找到15之后，需要回到根节点重新遍历查找，需要从根节点进行多次遍历，查询效率有待提高。

• 如果data存储的是行记录，行的大小随着列数的增多，所占空间会变大。这时，一个页中可存储的数据量就会变少，树相应就会变高，磁盘IO次数就会变大

所以接下来就引入我们的终极数据结构——B+树。

7、加强版多路平衡查找树(B+Tree)

B+树，作为B树的升级版，在B树基础上，MySQL在B树的基础上继续改造，使用B+树构建索引。B+树和B树最主要的区别在于非叶子节点是否存储数据的问题

• B树：非叶子节点和叶子节点都会存储数据。
• B+树：只有叶子节点才会存储数据，非叶子节点至存储键值。叶子节点之间使用双向指针连接，最底层的叶子节点形成了一个双向有序链表。

来看一下InnoDB里的B+树的具体存储结构：

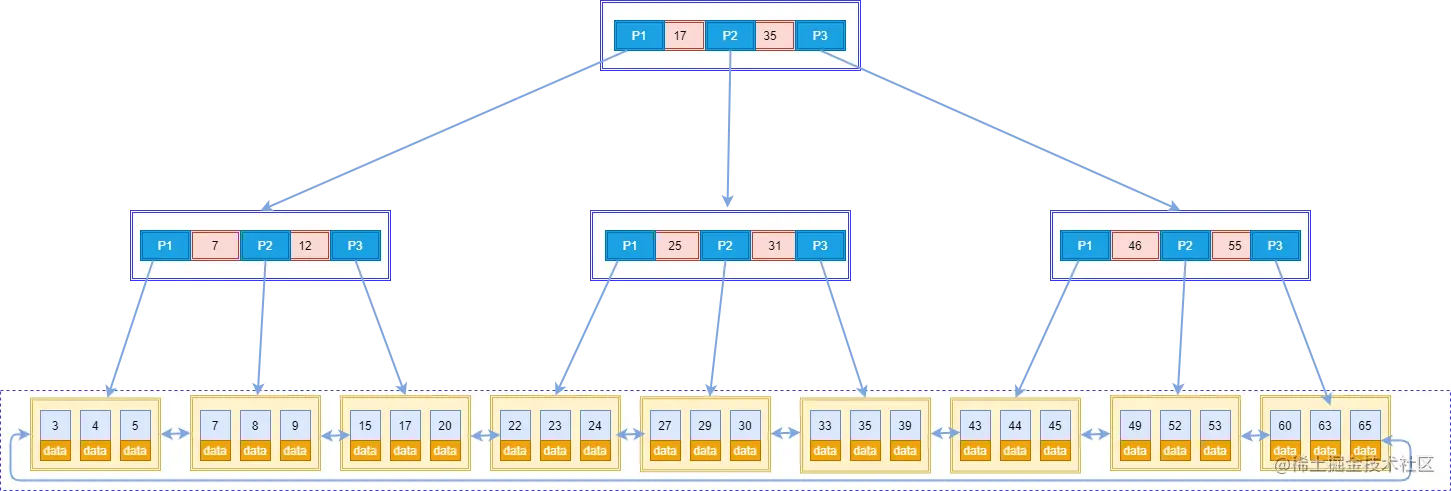
来说一下这张图的重点：

• 最外面的方块，的块我们称之为一个磁盘块，可以看到每个磁盘块包含几个数据项（粉色所示）和指针（黄色/灰色所示），如根节点磁盘包含数据项17和35，包含指针P1、P2、P3，P1表示小于17的磁盘块，P2表示在17和35之间的磁盘块，P3表示大于35的磁盘块。真实的数据存在于叶子节点即3、4、5……、65。非叶子节点只不存储真实的数据，只存储指引搜索方向的数据项，如17、35并不真实存在于数据表中。
• 叶子节点之间使用双向指针连接，最底层的叶子节点形成了一个双向有序链表。

7.1、存储容量

首先，查看 MySQL 默认一个节点页的大小：

SHOW GLOBAL STATUS like 'Innodb_page_size';

如下图：大小为 16K。

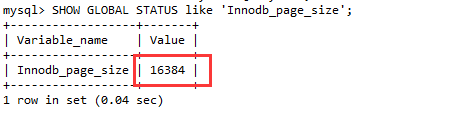
举个例子:假设一条记录是 1K，一个叶子节点(一页)可以存储 16 条记录。非叶子节点可以存储多少个指针?

假设索引字段是 bigint 类型，长度为 8 字节。指针大小在 InnoDB 源码中设置为 6 字节，这样一共 14 字节。非叶子节点(一页)可以存储 16384/14=1170 个这样的 单元(键值+指针)，代表有 1170 个指针。

树深度为 2 的时候，有 1170^2 个叶子节点，再假设最后一层，存放的数据 data 为 1k 大小（能存很多内容了），那么

A. 第一层最大节点数为： 16k / (8B + 6B) = 1170 (个)；

B. 第二层最大节点数也应为：1170 个；

C. 第三层最大节点数为：16k / 1k = 16 (个)。

可以存储的数据为 1170*1170*16=21902400。

在查找数据时一次页的查找代表一次 IO，也就是说，一张 2000 万左右的表，查询数据最多需要访问 3 次磁盘。

所以在 InnoDB 中 B+ 树深度一般为 1-3 层，它就能满足千万级的数据存储。

7.2、查询效率

我们来看一下 B+Tree 的数据搜寻过程:

1. 例如我们要查找 35，在根节点就找到了键值，但是因为它不是页子节点，所以会继续往下搜寻，25 是[17,35)的左闭右开的区间的临界值，所以会走中间的子节点，然 后继续搜索，它又是[28,34)的左闭右开的区间的临界值，所以会走左边的子节点，最后在叶子节点上找到了需要的数据。
2. 如果是范围查询，比如要查询从 22 到 60 的数据，当找到 22 之后，只需要顺着节点和指针顺序遍历就可以一次性访问到所有的数据节点，这样就极大地提高 了区间查询效率(不需要返回上层父节点重复遍历查找)。

3. 添加了指向相邻叶节点的指针**，形成了带有顺序访问指针的B+Tree，这样做是为了**提高区间查找的效率，只要找到第一个值那么就可以顺序的查找后面的值。

7.3、B+树特点总结

总结一下，InnoDB 中的 B+Tree 的特点:

1. 它是 B Tree 的变种，B Tree 能解决的问题，它都能解决。B Tree 解决的两大问题是什么?(每个节点存储更多关键字；路数更多)
2. 扫库、扫表能力更强(如果我们要对表进行全表扫描，只需要遍历叶子节点就可以 了，不需要遍历整棵 B+Tree 拿到所有的数据)
3. B+Tree 的磁盘读写能力相对于 B Tree 来说更强(根节点和枝节点不保存数据区， 所以一个节点可以保存更多的关键字，一次磁盘加载的关键字更多)
4. 排序能力更强(因为叶子节点上有下一个数据区的指针，数据形成了链表)
5. 效率更加稳定(B+Tree 永远是在叶子节点拿到数据，所以 IO 次数是稳定的)

参考：
https://juejin.cn/post/6935439646901927943