[LeetCode] 1368. Minimum Cost to Make at Least One Valid Path in a Grid 使网格图至少有一条有效路径的最小代价
Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:
1which means go to the cell to the right. (i.e go fromgrid[i][j]togrid[i][j + 1])2which means go to the cell to the left. (i.e go fromgrid[i][j]togrid[i][j - 1])3which means go to the lower cell. (i.e go fromgrid[i][j]togrid[i + 1][j])4which means go to the upper cell. (i.e go fromgrid[i][j]togrid[i - 1][j])
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
Return the minimum cost to make the grid have at least one valid path.
Example 1:
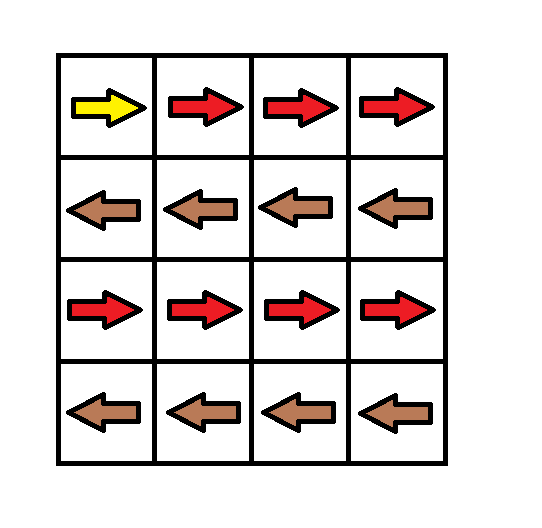
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
Example 2:
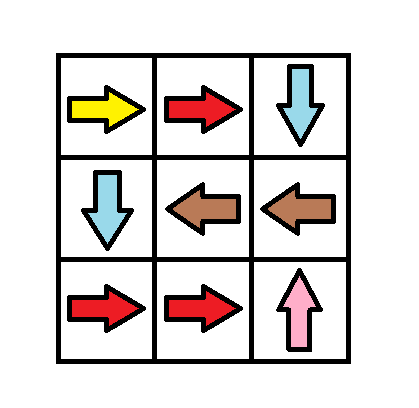
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).
Example 3:
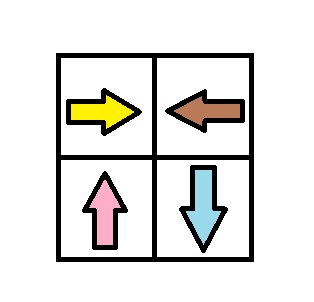
Input: grid = [[1,2],[4,3]]
Output: 1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1001 <= grid[i][j] <= 4
这道题说是给了一个 mxn 的二维数组,值为 1,2,3,4 中的数字,代表右,左,下,上,四个方向,说是如果按照指示的方向到下一个位置,就没有 cost,否则会有1个 cost。现在问以左上角为起点,走到右下角的终点最少需要多少个 cost。乍眼一看感觉像是个迷宫遍历求最短路径的问题,但是这道题求的却不是能到达终点的最少步数,而是问最小 cost,那么步数的多少和 cost 的大小并没有直接的联系,比如例子2中是把数组中的所有位置走了个遍,才能得到 cost 为0的最优解。
将这里箭头的方向看作是权重值为0的边,其他方向则是权重为1的边,则这里的数组就可以看作是有向权重图,求的就是单源点的最短路径了。当然在有向权重图里的最短路径就是权重和最小的路径,正好就是本题中的 cost,完美契合。此时就要祭出神器迪杰斯特拉算法 Dijkstra Algorithm 了,LeetCode 中使用了该算法的题目还有 Network Delay Time 和 The Maze II。Dijkstra 算法是以起点为中心,向外层层扩展,直到扩展到终点为止。
根据这特性,用 BFS 来实现时再好不过了,这里要先引入松弛操作 Relaxtion,这是这个算法的核心思想,当有条路径 (u, v) 是位置u到位置v,如果 cost(v) > cost(u) + w(u, v),那么 dist(v) 就可以被更新,这里的 cost(x) 就是从原点到达位置x的花费,w(u, v) 就是位置u和位置v的权重。在这道题中一般都是相邻的两个点进行比较,所以权重就是0或者1。这里使用 BFS 来进行遍历,首先创建一个代表方向的二维数组,顺序就按照题目中给定的顺序右,左,下,上,这样下标加1就是 grid 数组中的值了。然后还要建立一个二维数组 cost,这里 cost[i][j] 就表示从原点到达位置 (i, j) 的最小 cost,将 cost[0][0] 初始化为0,其他所有值初始化为 m + n - 2,这是因为就算每一步都增加1个花费,最多也就需要 m + n - 2 个花费就能到达终点。
接下来创建一个队列 queue,里面放二维坐标 encode 成的一维坐标,比如二维坐标 (i, j) 就可以通过 i * n + j 变成一维坐标,初始化把0加入队列中。接下来开始遍历,当队列不为空时进行循环,取出队首元素,并且还原出二维坐标 (i, j)。此时判断,若当前已经到达终点了,则用当前 cost[i][j] 更新结果 res,这里并不能直接返回 res,因为第一次到达终点时,并不能代表 cost 时最小的,所以是要遍历整个数组的。然后对当前位置的右,左,下,上,四个方向进行遍历,算出新的二维坐标,同时根据 grid 数组中的值算下要不要增加1个花费。之后进行判断,假如新的位置越界了,直接跳过;或者当前算出的 curCost 大于 cost 数组中的值,则也跳过,这个实际就是松弛操作; 或者 curCost 大于结果 res 时,也跳过,通过这个剪枝可以提高运行效率。否则就用 curCost 来更新 cost 数组中对应的位置,并把当前位置加入队列中,最终返回结果 res 即可,参见代码如下:
class Solution {
public:
int minCost(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size(), res = m + n - 2;
vector<vector<int>> dirs{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
vector<vector<int>> cost(m, vector<int>(n, m + n - 2));
cost[0][0] = 0;
queue<int> q{{0}};
while (!q.empty()) {
auto t = q.front(), i = t / n, j = t % n;
q.pop();
if (i == m - 1 && j == n - 1) {
res = min(res, cost[i][j]);
}
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k][0], y = j + dirs[k][1];
int curCost = grid[i][j] == k + 1 ? cost[i][j] : (cost[i][j] + 1);
if (x < 0 || x >= m || y < 0 || y >= n || curCost >= cost[x][y] || curCost >= res) continue;
cost[x][y] = curCost;
q.push(x * n + y);
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1368
类似题目:
Minimum Weighted Subgraph With the Required Paths
Disconnect Path in a Binary Matrix by at Most One Flip
参考资料:
https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/





 浙公网安备 33010602011771号
浙公网安备 33010602011771号