[LeetCode] 1344. Angle Between Hands of a Clock 时钟指针的夹角
Given two numbers, hour and minutes, return the smaller angle (in degrees) formed between the hour and the minute hand.
Answers within 10-5 of the actual value will be accepted as correct.
Example 1:
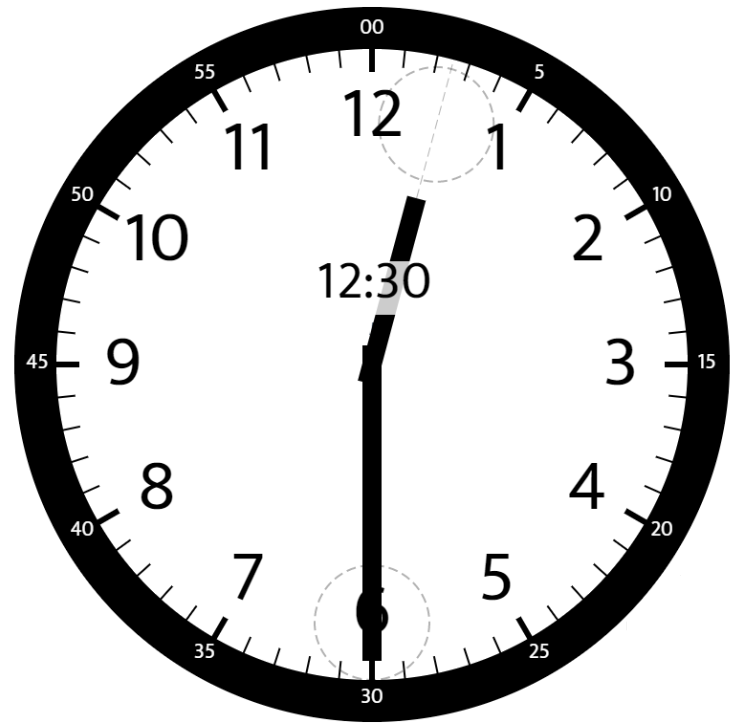
Input: hour = 12, minutes = 30
Output: 165
Example 2:
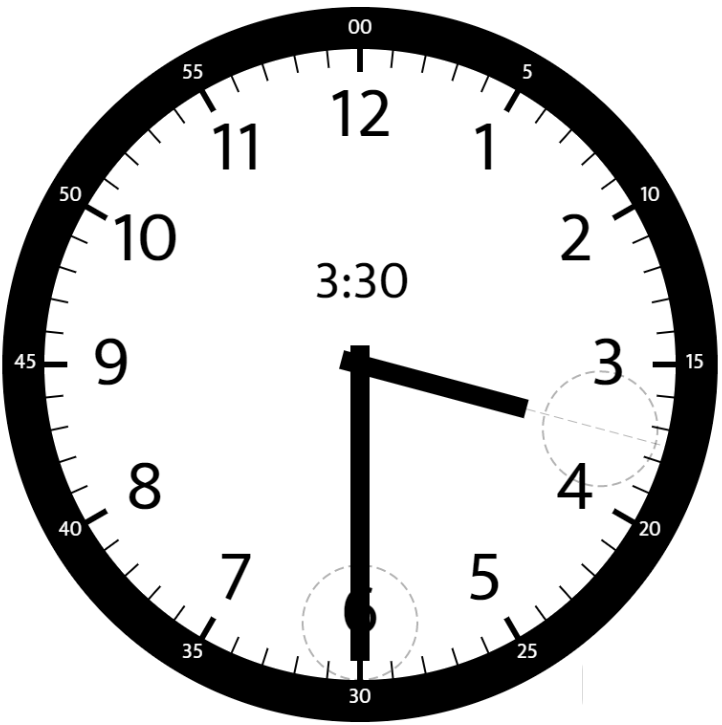
Input: hour = 3, minutes = 30
Output: 75
Example 3:
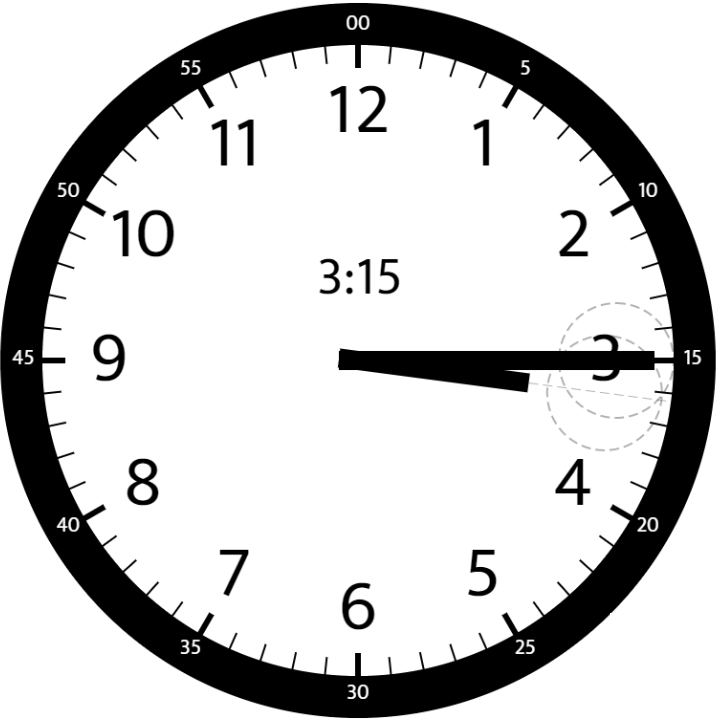
Input: hour = 3, minutes = 15
Output: 7.5
Constraints:
1 <= hour <= 120 <= minutes <= 59
这道题说给定了任意一个时间，让求时针分针之间的最小夹角。想必我们都对钟表都不陌生，一圈 360 度，一共 12 个数字，每两个数字之间为 30 度，有的表会在每两个数字之间分为五段，则每一段为6度。整点的夹角比较容易求，因为分针都指向 12，时针都精确地指向某个数字，比如六点整的时候时针分针夹角为 180 度。但对于任意时间，比如1点30分的时候，时针就指向数字1和2的正中间，时针的具体位置其实是根据分针指向的位置来确定的，分针走过的 360 度中的百分比，就等于时针走过的 30 度中的百分比。
这里以 12 点的位置为0度，则可以根据小时数先求出整点时的角度，这里由于 12 点就是0度，所以用个小 trick，hour 对 12 取余，然后再乘以 30，就是该小时数整点时的时针角度。然后再计算偏移量，根据分钟数除以60，再乘以 30 度，就是时针的偏移度数了。然后分针的角度就比较好算了，每一分钟的角度是6度，所以分钟数直接乘以6就行了。接下来算夹角，直接二者相减，并取绝对值，由于要返回最小的夹角，则跟其补角比较一下，返回较小值即可，参见代码如下：
class Solution {
public:
double angleClock(int hour, int minutes) {
double hourDegree = (hour % 12) * 30 + double(minutes) / 60 * 30;
double minDegree = minutes * 6;
double diff = abs(hourDegree - minDegree);
return min(diff, 360 - diff);
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1344
参考资料：
https://leetcode.com/problems/angle-between-hands-of-a-clock
