[LeetCode] 1329. Sort the Matrix Diagonally 将矩阵按对角线排序

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

Example 1:

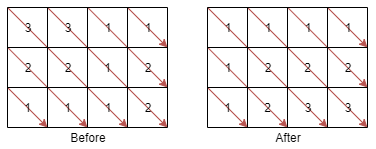
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

这道题让给一个矩阵的对角线排序，然后返回排序后的矩阵。对角线的排序可不像矩阵的行或者列排序那么容易，想要按顺序遍历对角线绝非易事，需要很复杂的坐标变换。这道题实际上考察了一个对角线坐标的性质，即处于同一条对角线上的点的横纵坐标的差均相同。这其实也不难理解，因为同一条对角线上的点可以看作是共线的，那么其斜率是相同的，则横纵坐标的差值一定相同。知道了这条性质后，对于任意一个坐标位置 (i, j)，就知道其属于 i-j 的那条对角线，于是可以建立一个差值和其对应的所有的点的映射，将同一条对角线上的所有点放到一个数组中，然后再对每个一个数组排序，注意这里是按从大到小排序，这样从后往前取就是所求的顺序了。之后再遍历一次矩阵，对于每一个位置 (i, j)，到 i-j 对应的集合中，取出当前最后的一个数字用来更新 mat[i][j] 即可，参见代码如下：

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        unordered_map<int, vector<int>> diagMap;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                diagMap[i - j].push_back(mat[i][j]);
            }
        }
        for (auto &a : diagMap) {
            sort(a.second.rbegin(), a.second.rend());
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                mat[i][j] = diagMap[i - j].back();
                diagMap[i - j].pop_back();
            }
        }
        return mat;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1329

参考资料：

https://leetcode.com/problems/sort-the-matrix-diagonally/

https://leetcode.com/problems/sort-the-matrix-diagonally/solutions/489749/java-python-straight-forward/

https://leetcode.com/problems/sort-the-matrix-diagonally/solutions/489775/c-elegant-map-solution-easy-to-understand/

LeetCode All in One 题目讲解汇总(持续更新中...)