[LeetCode] 1319. Number of Operations to Make Network Connected 连通网络的操作次数
There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [ai, bi] represents a connection between computers ai and bi. Any computer can reach any other computer directly or indirectly through the network.
You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.
Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.
Example 1:
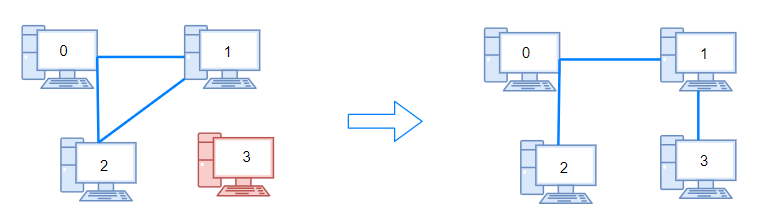
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.
Example 2:
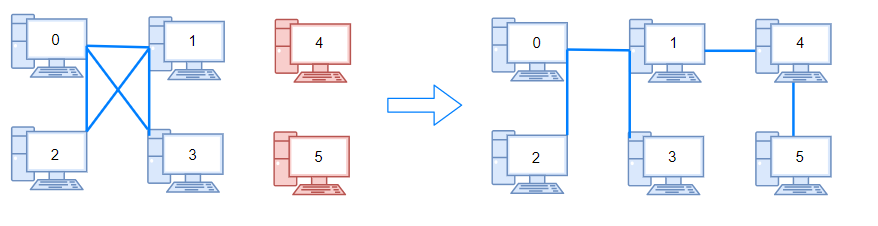
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2
Example 3:
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.
Constraints:
1 <= n <= 1051 <= connections.length <= min(n * (n - 1) / 2, 105)connections[i].length == 20 <= ai, bi < nai != bi- There are no repeated connections.
- No two computers are connected by more than one cable.
这道题说是有n台电脑,编号为0到 n-1。它们之间有些会有网线连接,现在说是可以将任意连着的网线断开,连到其他的位置,问为了使所有的电脑都连着,最少需要移动多少根网线(若无法连接所有电脑则返回 -1)。首先来分析一下什么情况下无法连接所有电脑,由于连接n台电脑最少需要 n-1 根网线,所以若给定的连接数少于 n-1,则可以直接返回 -1。再来分析一下什么情况下不用移动网线,即当前所有电脑已经都连接在一起了,若存在孤立的电脑,或者不同的群组,就需要移动网线了。这不由得让博主想起了之前的那道求岛屿个数的题 Number of Islands,这里也是类似,只要知道了有多少群组的电脑,就知道要移动的网线个数了,所以这道题就变成了求电脑群组的个数。
明白了要求什么,就来考虑数据结构和算法吧,其实就是个无向图,可以使用 DFS 来遍历,首先建立图的结构,这里可以使用邻接数组,其中 g[i] 表示所有和结点i相连的结点组成的数组。建立好邻接数组之后就可以开始遍历了,需要使用一个 visited 数组来记录访问过的结点,从结点0开始遍历,若该结点未被访问,则说明找到了一个新的群组,cnt 自增1,然后对该结点调用递归函数。在递归函数中,先对该结点标记为已访问,然后遍历和其所有相连的结点,对于未被访问过的结点再调用递归函数即可,这样就可以找到所有相连的结点了。最后计算出了群组个数 cnt 后,返回 cnt-1 即可,参见代码如下:
解法一:
class Solution {
public:
int makeConnected(int n, vector<vector<int>>& connections) {
if (connections.size() < n - 1) return -1;
int cnt = 0;
vector<vector<int>> g(n);
vector<bool> visited(n);
for (auto &c : connections) {
g[c[0]].push_back(c[1]);
g[c[1]].push_back(c[0]);
}
for (int i = 0; i < n; ++i) {
if (visited[i]) continue;
++cnt;
dfs(g, i, visited);
}
return cnt - 1;
}
void dfs(vector<vector<int>>& g, int i, vector<bool>& visited) {
visited[i] = true;
for (int next : g[i]) {
if (visited[next]) continue;
dfs(g, next, visited);
}
}
};
其实对于找群组的题目天然适合并查集 Union Find 的解法,LeetCode 中有很多道题都利用了这个解法。这里博主大致讲下该算法的原理,计算n个结点的群组的方法,首先假设这n个结点分别属于不同的群组,给它们依次分配一个 root 值:0到 n-1。这里还需要一个计算 root 值的函数 getRoot,对于相同群组的结点,其 root 值应该是相同的,若计算得出的 root 值不同,说明这两个点还没有被连接,此时更新其中一个结点的 root 值为另一个结点的 root 值,并且 cnt 自减1(这里 cnt 初始化为n,假设开始有n个群组)。接下来讲一下 getRoot 函数,需要传两个参数,root 数组和结点序号,此时判断,若该结点的 root 值与序号相同,则可直接返回序号值,否则需要对其 root 值再调用递归,为了提高计算效率,此时可以将该结点的 root 值更新为递归的返回值。通过使用 Union Find 的算法可以快速计算出群组个数 cnt, 返回 cnt-1 即可,参见代码如下:
解法二:
class Solution {
public:
int makeConnected(int n, vector<vector<int>>& connections) {
if (connections.size() < n - 1) return -1;
int cnt = n;
vector<int> root(n);
for (int i = 0; i < n; ++i) root[i] = i;
for (auto &c : connections) {
int x = getRoot(root, c[0]), y = getRoot(root, c[1]);
if (x != y) {
--cnt;
root[x] = y;
}
}
return cnt - 1;
}
int getRoot(vector<int>& root, int i) {
return (root[i] == i) ? i : (root[i] = getRoot(root, root[i]));
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1319
类似题目:
参考资料:
https://leetcode.com/problems/number-of-operations-to-make-network-connected/description/






 浙公网安备 33010602011771号
浙公网安备 33010602011771号