[LeetCode] 1263. Minimum Moves to Move a Box to Their Target Location 推箱子
A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an m x n grid of characters grid where each element is a wall, floor, or box.
Your task is to move the box 'B' to the target position 'T' under the following rules:
- The character
'S'represents the player. The player can move up, down, left, right ingridif it is a floor (empty cell). - The character
'.'represents the floor which means a free cell to walk. - The character
'#'represents the wall which means an obstacle (impossible to walk there). - There is only one box
'B'and one target cell'T'in thegrid. - The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
- The player cannot walk through the box.
Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.
Example 1:
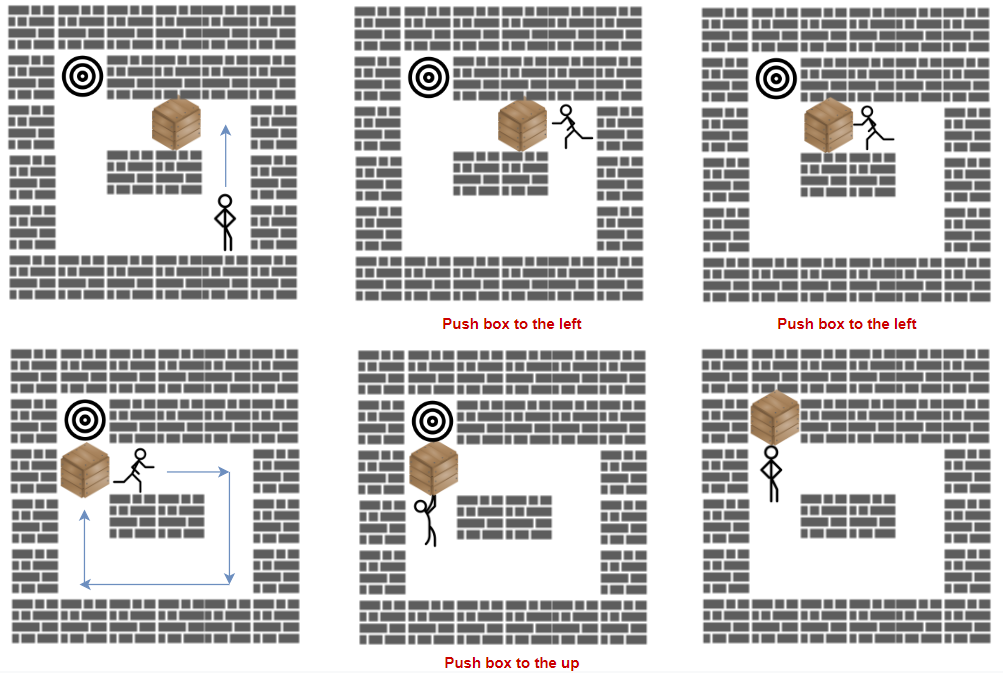
Input: grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.
Example 2:
Input: grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: -1
Example 3:
Input: grid = [["#","#","#","#","#","#"],
["#","T",".",".","#","#"],
["#",".","#","B",".","#"],
["#",".",".",".",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: 5
Explanation: push the box down, left, left, up and up.
Example 4:
Input: grid = [["#","#","#","#","#","#","#"],
["#","S","#",".","B","T","#"],
["#","#","#","#","#","#","#"]]
Output: -1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 20gridcontains only characters'.','#','S','T', or'B'.- There is only one character
'S','B', and'T'in thegrid.
这道题给了一个二维数组 grid,代表一个迷宫,里面有个人在推箱子,人的位置用字母S表示,箱子位置是B,需要将其推到位置T,迷宫中的点表示可以通行的区域,井号#表示墙,即不能通行的位置,问最少需要推几次才能把箱子推到目标位置。如果没有仔细读题目的话,很可能就把这题当成了一道普通的迷宫遍历问题了,但这是一道 Hard 题目,肯定不是随随便便一个 BFS 就能打发了题目。想想为什么要引入人推箱子这个设定,而且题目中还强调了人不能穿过箱子。箱子要移动,必须要有人去推才行,比如箱子要向左移动一格,则这个人一定要在箱子的右边,若接下来箱子想向下移动,则人一定要到箱子的上边,此时需要满足两个条件,一个是箱子的上边一定要是空着的,不能是障碍物,另一个是人必须能够到达上边的位置,也就是说即便箱子上方是空的,人若无法走到该位置的话,也是白搭,完全模拟了现实中的推箱子操作。
虽然说存在人推箱子这个设定,但这道题的本质还是迷宫遍历,求到达目标位置的最小步数还是首选广度优先遍历 Breadth-frist Search,不过此时的状态不再单单是箱子的位置,还应该包括人的位置,二者一起组成 BFS 中的状态,同时,要进入下一个状态的前提条件是,人必须要能够达到指定的推箱子的位置,这个判定就需要一个额外的 BFS 来做了,所以这道题实际需要写两个 BFS,是不是感觉很叼~先来写主 BFS 函数吧,需要用一个 queue 来遍历,根据前面的分析,每个状态由箱子和人的位置一起组成,所以 queue 里放一个 pair 对儿,注意这里把二维的位置坐标 encode 成一个整型数。用一个包含字符串的 HashSet 来记录访问过的状态,这里为了利用 HashSet 的常数级的查找效率,把状态的 pair 对儿又 encode 成了一个字符串。接下来要先遍历一遍数组 grid,找到箱子,人,还有目标点的位置,分别保存到 box,player,和 target 变量中,然后将这些非井号的字符都标记为点,表示是箱子可以通过的位置。
将箱子的起始位置和人的位置组成 pair 对儿加入 queue 中就可以开始 BFS 遍历了,由于要求最小步数,所以应该用层序的写法,在 while 循环的内部套一个 for 循环(必须写成初始化为 q.size() 的形式,而不能将其放到中间的判定部分,因为之后 queue 的大小会改变)。取出队首状态,得到箱子和人的位置,若此时箱子已经在目标位置了,则直接返回结果 res。否则就接着计算出箱子的横纵坐标,然后开始遍历其周围的四个位置,计算出箱子的新位置,同时也要计算出人推箱子需要站的位置,若这两个位置中任何一个位置越界或者是墙的话,则跳过当前循环,否则将箱子和人的新位置 encode 成一个字符串,在 HashSet 中查询,若已经存在了,则跳过,若不存在,还需要用另一个 BFS 来判断人是否能从之前的位置到达新的位置,把这个 BFS 放到一个单独的子函数中,就是经典的写法,这里就不单独讲了(唯一要注意的是遍历前要将箱子的位置标记成井号,因为人不能穿过箱子,最后返回结果前要复原)。若 BFS 返回 true 了,再把这个新状态排入队列 queue 中,并且加入 HashSet,每层遍历完之后,结果 res 自增1。若 while 循环退出了,说明无法推到目标位置,返回 -1 即可,参见代码如下:
class Solution {
public:
int minPushBox(vector<vector<char>>& grid) {
int res = 0, m = grid.size(), n = grid[0].size(), start = 0, target = 0, player = 0;
vector<vector<int>> dirs{{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
queue<pair<int, int>> q;
unordered_set<string> st;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'B') start = i * n + j;
else if (grid[i][j] == 'T') target = i * n + j;
else if (grid[i][j] == 'S') player = i * n + j;
if (grid[i][j] != '#') grid[i][j] = '.';
}
}
q.push({start, player});
while (!q.empty()) {
for (int i = q.size(); i > 0; --i) {
auto t = q.front(); q.pop();
int box = t.first, player = t.second;
if (box == target) return res;
int xbox = box / n, ybox = box % n;
for (auto dir : dirs) {
int x = xbox + dir[0], y = ybox + dir[1], xp = xbox - dir[0], yp = ybox - dir[1];
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == '#') continue;
if (xp < 0 || xp >= m || yp < 0 || yp >= n || grid[xp][yp] == '#') continue;
string str = to_string(box) + "_" + to_string(xp * n + yp);
if (st.count(str)) continue;
if (canReach(grid, player, xp * n + yp, box)) {
q.push({x * n + y, box});
st.insert(str);
}
}
}
++res;
}
return -1;
}
bool canReach(vector<vector<char>>& grid, int start, int target, int box) {
int m = grid.size(), n = grid[0].size();
queue<int> q{{start}};
vector<vector<int>> dirs{{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
vector<bool> visited(m * n);
visited[start] = true;
grid[box / n][box % n] = '#';
while (!q.empty()) {
int t = q.front(); q.pop();
if (t == target) {
grid[box / n][box % n] = '.';
return true;
}
int x0 = t / n, y0 = t % n;
for (auto &dir : dirs) {
int x = x0 + dir[0], y = y0 + dir[1];
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] != '.' || visited[x * n + y]) continue;
visited[x * n + y] = true;
q.push(x * n + y);
}
}
grid[box / n][box % n] = '.';
return false;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1263
参考资料:
https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/






 浙公网安备 33010602011771号
浙公网安备 33010602011771号