[LeetCode] 1104. Path In Zigzag Labelled Binary Tree 之字形二叉树路径
In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
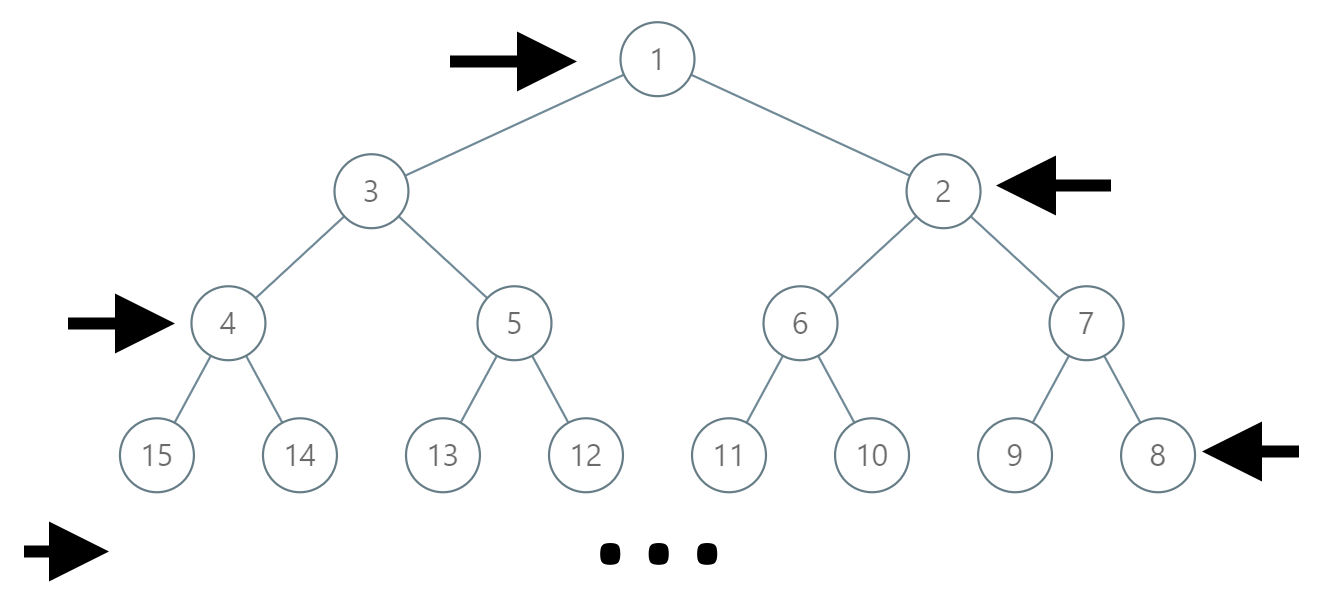
Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.
Example 1:
Input: label = 14
Output: [1,3,4,14]
Example 2:
Input: label = 26
Output: [1,2,6,10,26]
Constraints:
1 <= label <= 10^6
这道题说是有一棵无穷大的二叉树，结点值是从1开始按每层的顺序‘之’字形增长的，遇到奇数行，是从左到右增长，遇到偶数行，是从右到左增长。现在任意给一个结点值，让返回从根结点到该结点路径上的所有结点。题目中给的图片可以很好的帮助我们理解，由于是任意给的结点值，所以首先需要确定的是该结点位于第几层，这个不难计算，因为给定的一棵完全二叉树，所以每层的结点个数的确定的，通过和每层的总结点数比较，就可以知道当前的层数了。假如这棵二叉树不是按照‘之’字形排列的，那么某个结点的父结点值就是当前的结点值除以2得到。但是这里确实是‘之’字形排列的，怎么由当前结点得到父结点值呢？其实是该层的最大结点值加上最小结点值减去当前结点值并除以2，不要问博主为什么，因为博主也不知道（这里求大神们留言讲解啊），公众号上热心网友 那你很胖胖哦 留言给博主讲解了一下，这里直接摘抄过来啦，首先之字形和正常的完全二叉树比是奇数行相同，偶数行相反的。对于每一行，都有 min+max=current+(min+max-current)，因此这里实际上是做了一个取反的操作。max-current+1 可以得到当前节点是本行第几大的数，那么对于一个在偶数行的节点，(max-current+1)+(min-1) 可以算出这个节点如果按本行正序的话是哪个数，然后除以二取整，就得到了上一层奇数行的父节点值。对于一个在奇数行的节点，(max-current+1)+(min-1) 可以算出这个节点如果按本行逆序的话是哪个数，然后除以二取整，就得到了上一层偶数行的父节点值。由于奇偶行的处理是相同的，也可以直接合并起来，就不分奇偶了，用这个方法就可以快速的求出每层的父结点了，参见代码如下：
class Solution {
public:
vector<int> pathInZigZagTree(int label) {
int level = 0, cur = label;
while (1 << level <= label) ++level;
vector<int> res(level);
while (label >= 1) {
res[level - 1] = label;
label = (1 << level) - 1 - label + (1 << (level - 1));
label /= 2;
--level;
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1104
参考资料：
https://leetcode.com/problems/path-in-zigzag-labelled-binary-tree/
https://leetcode.com/problems/path-in-zigzag-labelled-binary-tree/discuss/323293/C%2B%2B-O(log-n)
