[LeetCode] 1080. Insufficient Nodes in Root to Leaf Paths 根到叶路径上的不足节点

Given the root of a binary tree, consider all root to leaf paths: paths from the root to any leaf.  (A leaf is a node with no children.)

A node is insufficient if every such root to leaf path intersecting this node has sum strictly less than limit.

Delete all insufficient nodes simultaneously, and return the root of the resulting binary tree.

Example 1:

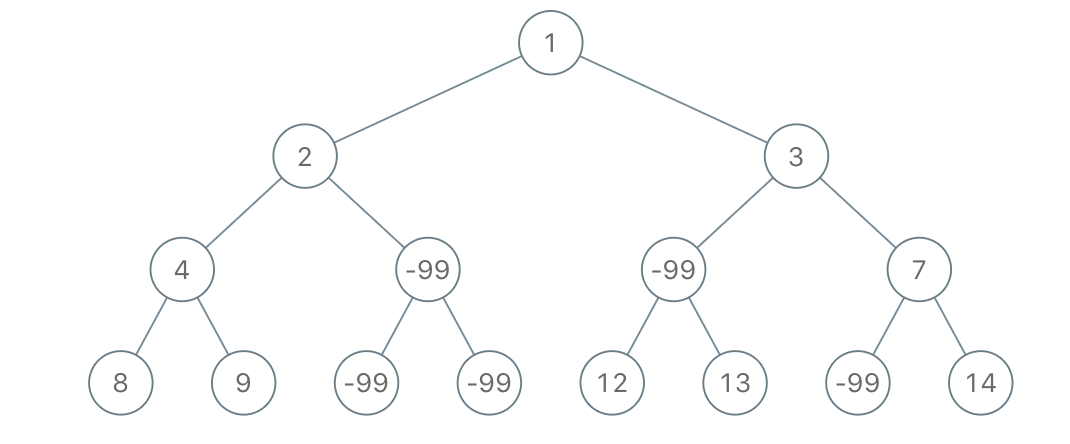
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1

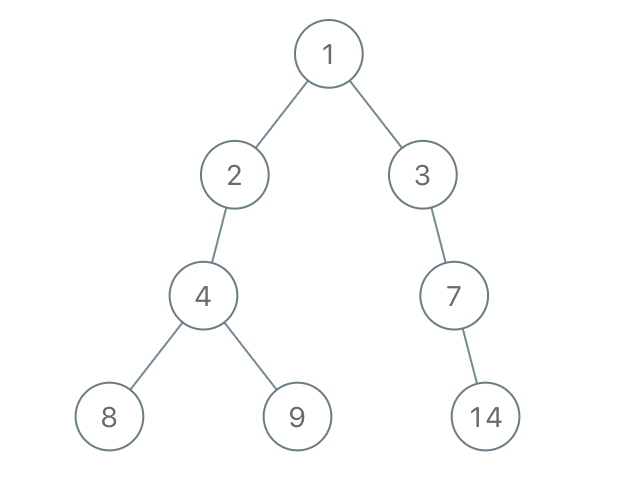
Output: [1,2,3,4,null,null,7,8,9,null,14]

Example 2:

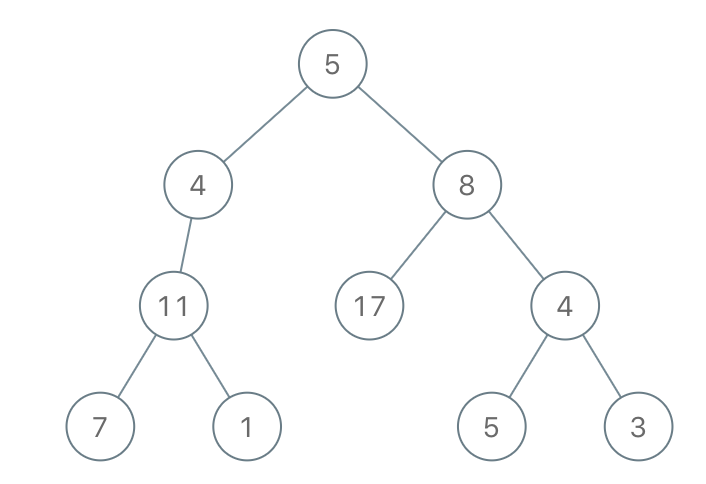
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22

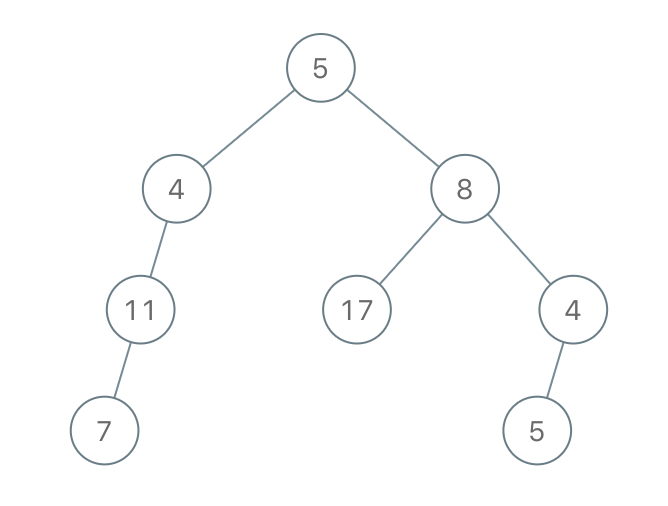
Output: [5,4,8,11,null,17,4,7,null,null,null,5]

Example 3:

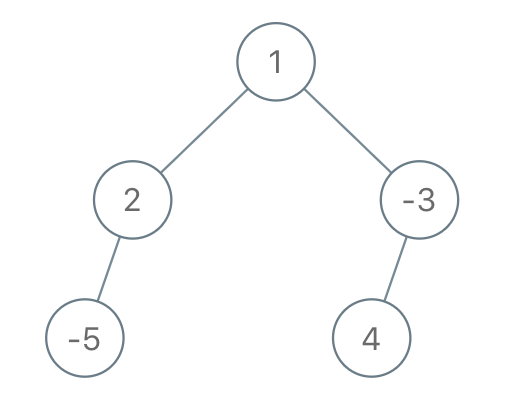
Input: root = [1,2,-3,-5,null,4,null], limit = -1

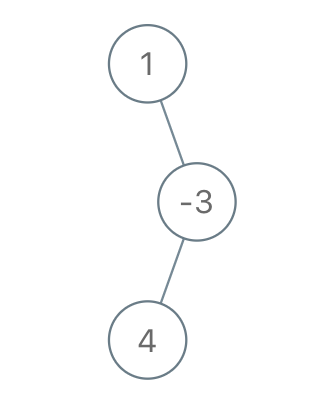
Output: [1,null,-3,4]

Note:

1. The given tree will have between 1 and 5000 nodes.
2. -10^5 <= node.val <= 10^5
3. -10^9 <= limit <= 10^9

这道题定义了一种不足结点，就是说经过该结点的所有根到叶路径之和的都小于给定的 limit，现在让去除所有的这样的不足结点，返回剩下的结点组成的二叉树。这题好就好在给的例子都配了图，能够很好的帮助我们理解题意，给的例子很好的覆盖了大多数的情况，博主能想到的唯一没有覆盖的情况就是可能根结点也是不足结点，这样的话有可能会返回空树。对于二叉树的问题，根据博主以往的经验，十有八九是要用递归来解的，而且往往写法很简洁，但是比较难想。这里首先处理一下 corner case，即根结点是叶结点的情况，这样只需要看根结点值是否小于 limit，是的话直接返回空指针，因为此时的根结点是个不足结点，需要被移除，否则直接返回根结点。一个比较快速的判断是否是叶结点的方法是看其左右子结点是否相等，因为只有均为空的时候才会相等。若根结点不为叶结点，且其左子结点存在的话，就对其左子结点调用递归，此时的 limit 需要减去根结点值，将返回的结点赋值给左子结点。同理，若其右子结点存在的话，就对其右子结点调用递归，此时的 limit 需要减去根结点值，将返回的结点赋值给右子结点。最后还需要判断一下，若此时的左右子结点都被赋值为空了，则当前结点也需要被移除，因为经过其左右子结点的根到叶路径就是经过该结点的所有路径，若其和均小于 limit，则当前结点也需要被移除，参见代码如下：

class Solution {
public:
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        if (root->left == root->right) {
            return root->val < limit ? nullptr : root;
        }
        if (root->left) {
            root->left = sufficientSubset(root->left, limit - root->val);
        }
        if (root->right) {
            root->right = sufficientSubset(root->right, limit - root->val);
        }
        return root->left == root->right ? nullptr : root;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1080

参考资料：

https://leetcode.com/problems/insufficient-nodes-in-root-to-leaf-paths/

https://leetcode.com/problems/insufficient-nodes-in-root-to-leaf-paths/discuss/308326/JavaC%2B%2BPython-Easy-and-Concise-Recursion

LeetCode All in One 题目讲解汇总(持续更新中...)