[LeetCode] 935. Knight Dialer 骑士拨号器
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
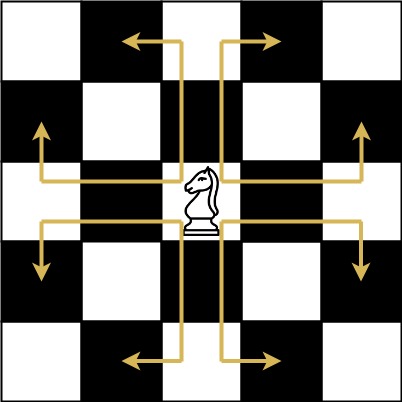
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).
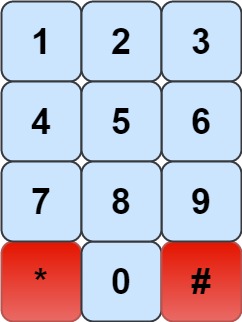
Given an integer n, return how many distinct phone numbers of length n we can dial.
You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.
As the answer may be very large, return the answer modulo 109 + 7.
Example 1:
Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
Example 2:
Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
Example 3:
Input: n = 3
Output: 46
Example 4:
Input: n = 4
Output: 104
Example 5:
Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.
Constraints:
1 <= n <= 5000
这道题说是有一种骑士拨号器,在一个电话拨号盘上跳跃,其跳跃方式是跟国际象棋中的一样,不会国际象棋的童鞋可以将其当作中国象棋中的马,马走日象飞田。这个骑士可以放在 10 个数字键上的任意一个,但其跳到的下一个位置却要符合其在国际象棋中的规则,也就是走日。现在给了一个整数N,说是该骑士可以跳N次,问能拨出多个不同的号码,并且提示了结果要对一个超大数字取余。看到这里,对于各位刷题老司机来说,肯定能反应过来要用动态规划 Dynamic Programming 了吧,因为数字可能巨大无比,强行暴力递归破解可能会爆栈。这里使用一个二维数组 dp,其中 dp[i][j] 表示骑士第i次跳到数字j时组成的不同号码的个数,那么最终所求的就是将 dp[N-1][j] 累加起来,j的范围是0到9。接下来看状态转移方程怎么写,当骑士在第i次跳到数字j时,考虑其第 i-1 次是在哪个位置,可能有多种情况,先来分析拨号键盘的结构,找出从每个数字能到达的下一个位置,可得如下关系:
0 -> 4, 6
1 -> 6, 8
2 -> 7, 9
3 -> 4, 8
4 -> 3, 9, 0
5 ->
6 -> 1, 7, 0
7 -> 2, 6
8 -> 1, 3
9 -> 4, 2
可以发现,除了数字5之外,每个数字都可以跳到其他位置,其中4和6可以跳到三个不同位置,其他都只能取两个位置。反过来想,可以去的位置,就表示也可能从该位置回来,所以根据当前的位置j,就可以在数组中找到上一次骑士所在的位置,并将其的 dp 值累加上即可,这就是状态转移的方法,由于第一步是把骑士放到任意一个数字上,就要初始化 dp[0][j] 为1,然后进行状态转移就行了,记得每次累加之后要对超大数取余,最后将 dp[N-1][j] 累加起来的时候,也要对超大数取余,参见代码如下:
解法一:
class Solution {
public:
int knightDialer(int N) {
int res = 0, M = 1e9 + 7;
vector<vector<int>> dp(N, vector<int>(10));
vector<vector<int>> path{{4, 6}, {6, 8}, {7, 9}, {4, 8}, {3, 9, 0}, {}, {1, 7, 0}, {2, 6}, {1, 9}, {4, 2}};
for (int i = 0; i < 10; ++i) dp[0][i] = 1;
for (int i = 1; i < N; ++i) {
for (int j = 0; j <= 9; ++j) {
for (int idx : path[j]) {
dp[i][j] = (dp[i][j] + dp[i - 1][idx]) % M;
}
}
}
for (int i = 0; i < 10; ++i) res = (res + dp.back()[i]) % M;
return res;
}
};
我们也可以用递归+记忆数组的方式来写,整体思路和迭代的方法并没有什么区别,之前类似的题目也不少,就不多解释了,可以对照上面的讲解和代码来理解,参见代码如下:
解法二:
class Solution {
public:
int knightDialer(int N) {
int res = 0, M = 1e9 + 7;
vector<vector<int>> memo(N + 1, vector<int>(10));
vector<vector<int>> path{{4, 6}, {6, 8}, {7, 9}, {4, 8}, {3, 9, 0}, {}, {1, 7, 0}, {2, 6}, {1, 9}, {4, 2}};
for (int i = 0; i < 10; ++i) {
res = (res + helper(N - 1, i, path, memo)) % M;
}
return res;
}
int helper(int n, int cur, vector<vector<int>>& path, vector<vector<int>>& memo) {
if (n == 0) return 1;
if (memo[n][cur] != 0) return memo[n][cur];
int res = 0, M = 1e9 + 7;
for (int idx : path[cur]) {
res = (res + helper(n - 1, idx, path, memo)) % M;
}
return memo[n][cur] = res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/935
类似题目:
Letter Combinations of a Phone Number
参考资料:
https://leetcode.com/problems/knight-dialer/
https://leetcode.com/problems/knight-dialer/discuss/189265/Concise-Java-DP-Solution
https://leetcode.com/problems/knight-dialer/discuss/189271/Java-Top-Down-Memo-DP-O(N)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号