2021牛客寒假算法训练营3题解（9/10）

2021牛客寒假训练营3题解

A.模数的世界

题目链接：A.模数的世界

相关：数论

参考题解：https://ac.nowcoder.com/discuss/594509?type=101&channel=-1&source_id=0

引用题解的结论（自己太菜，推不出来。。。）：

对于最大值，可以猜想除非a == b == 0时最大值为0，此时x == y == p；否则最大值一定为p - 1

假设a >= b

1. 当b == 0 && a != 0时，x = (p - a) * (p - 1); y = (p - b) * (p - 1)

2. 当a != 0 && b != 0时：

   由\(k_1 * (p-1) \% p = a\) 和\(k_2 * (p-1) \% p = b\) 可得k1 = (p - a), k2 = (p - b) 此时\(k_1 \leq k_2\)，且\(k_1 和 k_2\)可能并不互质

   此时设x = (m * p + k1) * (p - 1), y = k2 * (p - 1)

   注意到k2!=0且 k2 必然和 p 互质，那么 mp+nk2=1 必有解。利用exgcd解出系数，并让m大于0,此时该式子等价于$ m*p\equiv1(mod\ k2) $。构造((k2 + 1 - k1) * m * p + k1) * (p - 1) = x, k2 * (p - 1) = y为解,可证满足上述方程，且二者gcd为p-1。

代码：

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

int t;

LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    
    return d;
}

int main()
{
    cin >> t;
    
    while(t--)
    {
        LL a, b, p, ra, rb, k1, k2, x, y;
        scanf("%lld%lld%lld", &a, &b, &p);
        if(!a && !b) printf("0 %lld %lld\n", p, p);
        else if(!a || !b) 
        {
            ra = (p - a)*(p - 1);
            rb = (p - b)*(p - 1);
            printf("%lld %lld %lld\n", p - 1, ra, rb);
        }
        else
        {
            bool flag = false;
            if(a < b) swap(a, b), flag = true;
            k1 = p - a, k2 = p - b;
            exgcd(p, k2, x, y);
            if(x < 0) x = (x % k2 + k2) % k2;
            ra = ((k2 + 1 - k1) * x * p + k1) * (p - 1);
            rb = k2 * (p - 1);
            if(flag) swap(ra, rb);
            printf("%lld %lld %lld\n", p - 1, ra, rb);
        }
    }
    
    return 0;
}

B.内卷

题目链接：B.内卷

相关：尺取法

待补。。。

C.重力坠击

题目链接：C.重力坠击

相关：搜索（DFS）、数学

题目数据不大，枚举每一个点，记录最大值即可。注意去重

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>

using namespace std;

const int N = 11, M = 20;

int n, k, R, ans;
bool bat[N], back_bat[4][N];

struct Enemy
{
    int x, y, r;
}e[N];

int check(int x, int y)
{
    int res = 0;
    for(int i = 0; i < n; i++)
        if(!bat[i])
        {
            int a = e[i].x, b = e[i].y, r = e[i].r;
            int dist = (a-x)*(a-x) + (b-y)*(b-y);
            if(dist <= (r + R) * (r + R)) 
            {
                res++;
                bat[i] = true;
            }
        }
    return res;
}

void dfs(int num, int at)
{
    if(num == k)
    {
        ans = max(ans, at);
        return ;
    }
    for(int i = -7; i <= 7; i++)
        for(int j = -7; j <= 7; j++)
        {
            memcpy(back_bat[num], bat, sizeof bat);
            dfs(num+1, at + check(i, j));
            memcpy(bat, back_bat[num], sizeof bat);
        }
}

int main()
{
    cin >> n >> k >> R;
    for(int i = 0; i < n; i++)
    {
        int x, y, r;
        scanf("%d%d%d", &x, &y, &r);
        e[i] = {x, y, r};
    }
    
    dfs(0, 0);
    cout << ans << endl;
    
    return 0;
}

D. Happy New Year!

题目链接：D. Happy New Year!

签到题

代码：

#include <iostream>

using namespace std;

string s;

int main()
{
    int x;
    cin >> x;
    if(x % 10) cout << x-1+10 << endl;
    else cout << (x/1000)*1000 + 100 + ((x % 100)/10 - 1) << endl;
    
    return 0;
}

E.买礼物

题目链接：E.买礼物

相关：线段树

第一次线段树实战演练，掌握十分不牢靠

由题意分析可得：实际是要模拟一下链表的操作，用last[i]记录a[i]前面第一个等于自己的位置，不存在则置0；用ne[i]记录a[i]后面第一个等于自己的位置，不存在则置n+1。

对于购买操作：

void del(int x)
{
    ne[last[x]] = ne[x];
    last[ne[x]] = last[x];
    last[x] = 0;
    ne[x] = n+1;
}

对于询问操作：

查询区间[l, r]中最小的ne[i]，判断其是否小于等于r，小于等于则输出1， 否则输出0。(也可以查询最大的last[i]是否大于等于l)

如果每次询问都是暴力查询，则会TLE， 所以要用到线段树维护区间的最小ne[]，实现单点修改，区间查询。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 5e5+10, M = 1e6+10, INF = 0X3f3f3f3f;

int n, q;
int a[N];
int last[N], ne[N], pos[M];

struct Node
{
    int l, r, v;
}tr[4 * N];

void pushup(int u)
{
    tr[u].v = min(tr[u << 1].v, tr[u << 1 | 1].v);
}

void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if(l == r) 
    {
        tr[u].v = ne[l];
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
} 

void modify(int u, int x, int v)
{
    if(tr[u].l == x && tr[u].r == x) tr[u].v = v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    
    int mid = tr[u].l + tr[u].r >> 1;
    int v = INF;
    if(l <= mid) v = query(u << 1, l, r);
    if(r > mid) v = min(v, query(u << 1 | 1, l, r));
    return v;
}

void del(int x)
{
    ne[last[x]] = ne[x];
    last[ne[x]] = last[x];
    last[x] = 0;
    ne[x] = n+1;
}

int main()
{
    cin >> n >> q;
    for(int i = 1; i <= n; i++)
    {
        last[i] = 0, ne[i] = n+1;
        scanf("%d", &a[i]);
        if(pos[a[i]]) 
        {
            last[i] = pos[a[i]];
            ne[pos[a[i]]] = i;
        }
        pos[a[i]] = i;
    }
    
    build(1, 1, n);
/*    puts("");
    for(int i = 1; i <= 9; i++)
            cout << tr[i].l <<',' << tr[i].r <<  ':' << tr[i].v << endl;*/
    while(q--)
    {
        int op, x, l, r;
        scanf("%d", &op);
        if(op == 1)
        {
            scanf("%d", &x);
            modify(1, x, n+1);
            modify(1, last[x], ne[x]);
            del(x);
        }
        else 
        {
            scanf("%d%d", &l, &r);
            printf("%d\n", query(1, l, r) <= r ? 1 : 0);
        }
    }
    return 0;
}

F.匹配串

题目链接：F.匹配串

相关：字符串

因为每个字符串都至少含有一个'#'，所以答案只有0和-1。

可以预处理出每个字符串第一个'#'的前缀和最后一个'#'的后缀，然后逐一比对，如果每个前后缀都是最长的那个前后缀的子串，那么答案为-1， 否则为0。

代码：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e6+10;

int n;
string s[N];
int lma = 0, rma = 0;
vector<PII> l_r;

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> s[i];;
        int a = 0, b = s[i].length() - 1;
        for(int j = 0; j <= b; j++)
            if(s[i][j] == '#')
            {
                a = j-1;
                break;
            }
        for(int j = b; ~j; j--)
            if(s[i][j] == '#')
            {
                b = b - j;
                break;
            }
        l_r.push_back({a, b});
        lma = max(lma, a);
        rma = max(rma, b);
    }
    
    for(int i = 0; i <= lma; i++)
        for(int j = 0; j < n - 1; j++)
            if(s[j][i] != s[j+1][i] && i <= l_r[j].first && i <= l_r[j+1].first)
            {
                cout << 0 << endl;
                return 0;
            }
    
    for(int i = 1; i <= rma; i++)
        for(int j = 0; j < n-1; j++)
            if(s[j][s[j].length()-i] != s[j+1][s[j+1].length()-i] && i <= l_r[j].second && i <= l_r[j+1].second)
            {
                cout << 0 << endl;
                return 0;
            }
    
    cout << -1 << endl;
    
    return 0;
}

G.糖果

题目链接：G.糖果

相关：搜索（dfs、bfs)、连通块

根据题意将每个小朋友作为顶点，两人是朋友则连一条无向边，建图。题目即可转化为求每个连通块的点数和最大糖果数，答案即为：

\(\sum{点数*最大糖果数}\)

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

typedef long long LL;

using namespace std;

const int N = 1e6+10;

int n, m, a[N];
int h[N], e[N*2], ne[N*2], idx;
bool st[N];
LL ans;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dfs(int x, int &ma, int &num)
{
    queue<int> q;
    q.push(x);
    ma = max(a[x], ma);
    num++;
    st[x] = true;
    
    while(q.size())
    {
        int t = q.front();
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(!st[j])
            {
                num++;
                ma = max(ma, a[j]);
                q.push(j);
                st[j] = true;
            }
        }
    }
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    memset(h, -1, sizeof h);
    for(int i = 1; i <= m; i++)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
    }
    
    for(int i = 1; i <= n; i++) 
    {
        int ma = 0, num = 0;
        if(!st[i]) dfs(i, ma, num);
 //       cout << ma << ' ' << num << endl;
        ans += (LL)ma * num;
    }
    
    cout << ans << endl;
    
    return 0;
}

H.数字串

题目链接：H.数字串

相关：字符串处理、模拟

考虑两种情况即可：字符是否可以拆分（如：k为11，可拆分为aa）,两个字符是否可以合并（如：aa为11，可合并为k）

两种情况任意一种被执行一次即可

特别注意：10、20不可拆分，也不可参与合并

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

string s, t, ans;
bool ok;

string ctn(char c)
{
    return to_string(c - 'a' + 1);
}

string ntc(string n)
{
    string res = "";
    res += 'a' + stod(n) - 1;
    return res;
}

int main()
{
    cin >> s;
    int ls = s.length();
    for(int i = 0; i < ls; i++)
    {
        if(!ok)
        {
            char c = s[i];
            t += ctn(c);
//            cout << c << ' ' << t << ' ' << ans << endl;
            if(t.length() == 2 && (t[0]-'0') * 10 + (t[1]-'0') <= 26 && t[1] != '0')
            {
                //分
                if(c > 'j')
                {
                    string t0 = "", t1 = "";
                    t0 += t[0];
                    t1 += t[1];
                    ans += ntc(t0);
                    ans += ntc(t1);
 //                   cout << "ok:" << ok << ' ' << t0 << ' ' << t1  << ' ' << ans << endl;
                }
                else ans += ntc(t); //合
                ok = true;
            }
            else if(t.length() == 3 && t[2] != '0')
            {
                string t0 = "", t1 = "";
                t0 += t[0];
                t0 += t[1];
                t1 += t[2];
//                cout << t0 << ' ' << t1 << endl;
                ans += ntc(t0);
                ans += ntc(t1);
                ok = true;
//                cout << ok << ' ' << ans << endl;
            }
            else if(t[0] > '2' || t.length() == 2 && t[1] == '0')
            {
                ans += s[i];
                t = "";
            }
            else if((t[0]-'0') * 10 + (t[1]-'0') > 26 || t.length() == 3 && t[2] == '0')
            {
                ans += s[i-1];
                ans += s[i];
                t = "";
            }
        }
        else ans += s[i];
    }
//    cout << ok << endl;
    if(ok) cout << ans << endl;
    else cout << -1 << endl;
    
    return 0;
}

I.序列的美观度

题目链接：I.序列的美观度

相关：动态规划、优化

感觉和最长上升子序列很像，然后推出来的DP做法是对的，但是时间复杂度为O(N²)，很明显超时了，需要优化

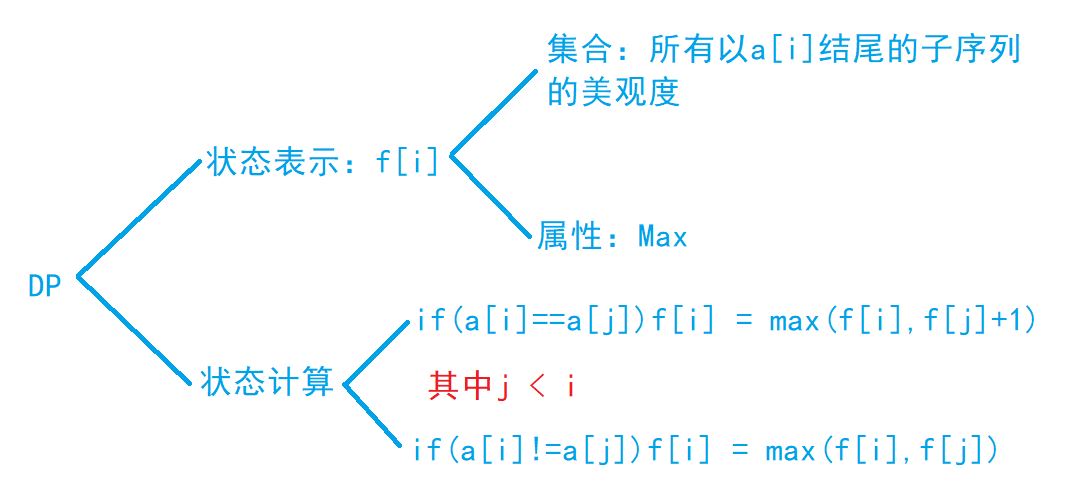
对于两种情况：

• a[i] != a[j]：f[i] = max(f[i], f[j])，是用f[1]~f[i-1]中的最大值来更新f[i]， 所以在求每个f[i]的时候可以用一个ma变量来存最大值，这样状态转移方程即可变为：f[i] = ma
• a[i] == a[j]：f[i] = max(f[i], f[j]+1)，这里可以直接去a[i]前最后一个与其相等的位置的f[j]来更新，然后我们可以通过一个pos[]数组来记录前一个和当前位置值相等的位置，这样状态转移方程即可变为：f[i] = max(ma, f[pos[a[i]]] + 1)

经过这两个优化，时间复杂度变为O(n)

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e6+10;

int n, ans;
int a[N], pos[N], f[N];

int main()
{
    cin >> n;
    
    int ma = 0;
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        if(!pos[a[i]]) f[i] = ma;
        else f[i] = max(f[pos[a[i]]] + 1, ma);
        ma = max(ma, f[i]);
        pos[a[i]] = i;
    }
    cout << ma << endl;
    
    return 0;
}

J.加法和乘法

题目链接：J.加法和乘法

相关：博弈论、找规律

• 对加法：奇数+奇数=偶数，奇数+偶数=奇数，偶数+偶数=偶数
• 对乘法：奇数*奇数=奇数，奇数*偶数=偶数，偶数*偶数=偶数

关键在于最后一次操作，如果n为奇数，则n-1为偶数，牛妹进行最后一次，反之牛牛进行最后一次操作

首先，对于以后一次操作，无论剩余的两个数的奇偶性，一定可以变成一个偶数，所以如果牛妹是最后一次操作（n为奇数）则必赢

对于牛牛最后一次操作（n为偶数）,当且仅当最后两个数至少有一个奇数时，牛牛才能赢。所以对于牛妹，最优策略是想办法把奇数全部消去；对牛牛，最优策略是想办法保留至少一个奇数。根据上面的加乘法规律可得，奇数可以消去但无法增加，最多可以一次消去2个。

在n为偶数的情况下，牛妹一共可以操作\((n-2)/2\)次，在不考虑奇偶数个数的情况下，牛妹最多只能消去n-2个奇数，所以当给出的数中奇数个数大于n-2时，牛牛可以获胜。

注意特判n=1的情况。

代码：

#include <iostream>

using namespace std;

int n, ji;

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        if(x & 1) ji++;
    }
    if(n == 1 && ji || !(n&1) && ji > n-2) puts("NiuNiu");
    else puts("NiuMei");
    return 0;
}