2021牛客寒假算法训练营1题解（9/10）

2021牛客寒假训练营1题解

A、串

题目链接：A.串

相关：DP、快速幂

解法一：

f[i]：长度为i的含“us”的字符串个数

1. 前i-1个字符中含"us"：26 * f[i-1]
2. 前i-1个字符中含"u"不含"us"：总数 - 不含"u"的 - 含"us"的 = \(26^{i-1}-25^{i-1}-f[i-1]\)

综上：$ f[i] = 26^{i-1} - 25^{i-1} + 25 * f[i-1]$

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2e6+10, mod = 1e9+7;

int n;
long long a[N], ans = 1;

long long quick_pow(int a, int b)
{
    long long res = 1;
    while(b)
    {
        if(b & 1) res = res * a % mod;
        b >>= 1;
        a = (long long)a * a % mod;
    }
    
    return res % mod;
}

int main()
{
    cin >> n;
    a[2] = 1;
    for(int i = 3; i <= n; i++)
    {
        //暂时不明白为什么要加一个mod
        a[i] = (quick_pow(26, i-1) - quick_pow(25, i-1) + 25*a[i-1] + mod) % mod;
        ans = (ans + a[i]) % mod;
    }
    
    cout << ans << endl;
    
    return 0;
}

解法二：

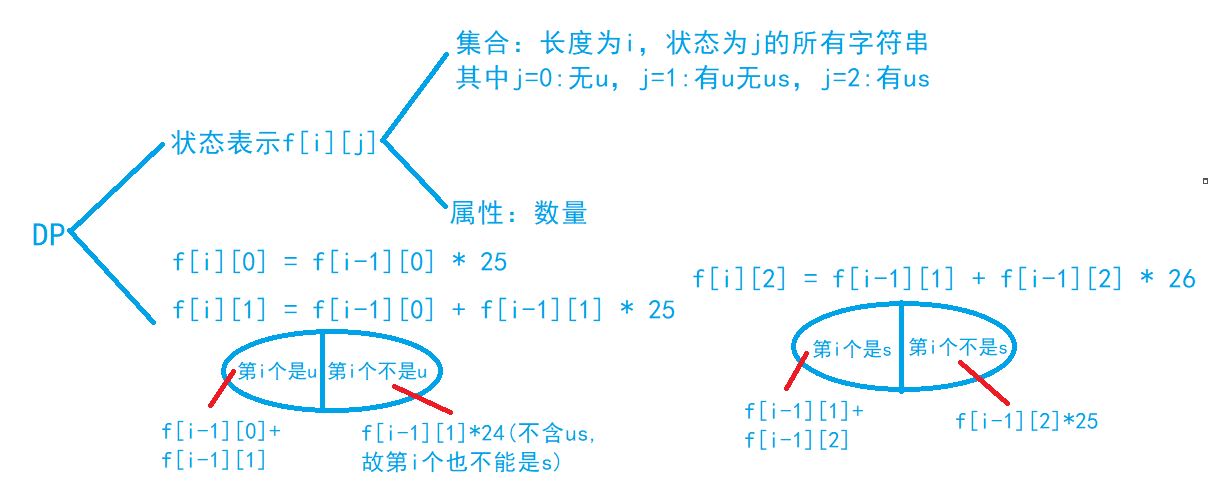
代码：

#include <iostream>

using namespace std;

const int N = 2e6+10, mod = 1e9+7;

int n;
long long ans, f[N][3];

int main()
{
    cin >> n;
    f[1][0] = 25;
    f[1][1] = 1;

    for(int i = 2; i <= n; i++)
    {
        f[i][0] = (f[i-1][0] * 25) % mod;
        f[i][1] = (f[i-1][0] + f[i-1][1] * 25) % mod;
        f[i][2] = (f[i-1][1] + f[i-1][2] * 26) % mod;
        ans = (ans + f[i][2]) % mod;
    }
    cout << ans << endl;
    
    return 0;
}

B、括号

题目链接：B.括号

相关：找规律、构造

写几对括号可以发现：

()    :1 = 1
()()  :3 = 2 + 1
()()():6 = 3 + 2 + 1
......

进一步观察可以发现：在第i对括号后面加1个')'， 括号的数量就会加i .

由此导出做法：

1. 预处理出画几对括号会生成多少对括号：a[i] = 1 + 2 + ... + i
2. 二分出小于等于k的最大a[l]
3. 为了尽量让总长度短一些，倒序求出需要在第i对括号后面添加rk[i]个')'
4. 输出答案

代码：

#include <iostream>
#include <algorithm>
#include <string>

using namespace std;

const int N = 5e4+10;

int a[N], rk[N];

int main()
{
    int k;
    cin >> k;
    //预处理
    for(int i = 1; i < N; i++) a[i] = a[i-1] + i;
    //二分
    int l = 0, r = N;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if(a[mid] <= k) l = mid;
        else r = mid - 1;
    }
    //倒序求需添加的')'数量
    int num = k - a[l];
    for(int i = l; i && num; i--) 
    {
        rk[i] = num / i;
        num = max(0, num - i * (num / i));
    }
    //按题意输出答案
    if(k)
    {
        for(int i = 1; i <= l; i++) 
        {
            printf("()");
 //           cout << rk[i] << endl;
            for(int j = 1; j <= rk[i]; j++) printf(")");
        }
        puts("");
    }
    else cout << "(" << endl;
    
    return 0;
}

C、红和蓝

题目链接：C.红和蓝

参考题解：https://blog.nowcoder.net/n/32e7a9e7caa3422286109ab0b3fabf37

题意：给一颗树的节点染红蓝两种色，满足每个节点的相邻节点有且仅有一个节点的颜色和当前节点相同

首先考虑最特殊的节点——叶子节点，与叶子节点相邻的仅有其父节点一个节点，所以叶子节点一定和其父节点颜色相同。

将所有的叶子节点和其父节点标记后，剩余的树又会出现新的叶子结点，重复步骤使整棵树全部被标记，然后根据标记是否相同染上相应的颜色。

如果出现标记时父节点已经被标记（重复标记）或者仅有根节点一个节点则无法完成染色。

解法：两遍dfs(), 第一遍打标记，第二遍染颜色

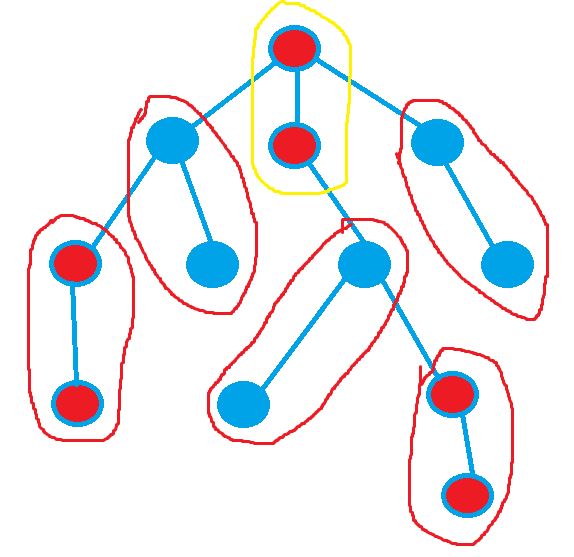
代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 1e5+10;

int n;
int h[N], e[2 * N], ne[2 * N], idx;
//f[]:标记，color[]:颜色（1：R， 2：B)
int f[N], color[N], cnt;
bool flag = true;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
//第一遍dfs给所有点打上标记
//参数：x-当前节点，fa-当前节点的父节点
void dfs1(int x, int fa)
{
    //记录儿子数量
    int son = 0;
    //遍历所有儿子
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        //由于是双向边，“父节点也在儿子节点中”，特殊处理去掉
        if(j == fa) continue;
        son++;
        dfs1(j, x);
    }
    //如果当前节点是叶子节点(儿子数量为0),或者当前节点并没有被标记
    if(!son || !f[x])
    {
        //如果父节点已经有标记了，说明不可能完成染色
        if(f[fa])
        {
            flag = false;
            return;
        }
        //给当前节点和父节点打上相同的标记
        f[x] = f[fa] = ++cnt;
    }
}
//如果顺利给所有点打上标记，则第二遍dfs根据标记涂上颜色
//参数：x-当前节点，fa-当前节点的父节点
void dfs2(int x, int fa)
{
    //遍历儿子节点
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        //去掉儿子节点中的父节点
        if(j == fa) continue;
        //如果当前节点和子节点标记相同，则染上相同的颜色
        //否则染上不同的颜色
        if(f[j] == f[x]) color[j] = color[x];
        else color[j] = color[x] ^ 1;
        dfs2(j, x);
    }
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for(int i = 0; i < n-1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    
    dfs1(1, 0);
    if(f[0] != 0 || !flag)
    {
        cout << -1 << endl;
        return 0;
    }
    color[1] = 1;
    dfs2(1, 0);
    for(int i = 1; i <= n; i++)
        if(color[i] == 1) printf("R");
        else printf("B");
    
    return 0;
}

D、点一成零

题目链接：D.点一成零

参考题解：https://blog.nowcoder.net/n/4e45b3189c564001b186775f7ea43ec4

相关：维护size的并查集、快速幂求逆元

在初始状态下：有x个连通块，如果每个连通块只能点1个，总共有x!种， 而每个连通块有size个可以点，所以$ans = x! * (每个连通块1的个数的乘积) $

对于每次操作：

1. 如果当前位置已经是‘1’，矩阵和答案均不会发生改变

2. 如果当前位置是‘0’，先假设其是一个单独的连通块cnt++​，先行更新答案$ ans = ans * cnt * 1$， 然后检查与其相邻的四个位置

   • 如果该位置不是1，无影响

   • 如果该位置是1，且与当前点已经在并查集的同一个连通块中了，无影响

   • 如果该位置是1，且与当前点不在并查集的同一个连通块中，则要把当前点和该位置的连通块合并，更新答案：

     连通块数量-1：\(ans = (ans / cnt) \% mod\) (分数取模)，注意cnt--

     将两个连通块的大小除去：\(ans = ans / size1，ans = ans / size2\)

     将新的连通块大小乘进去：\(ans = ans * (size1 + size2)\)

代码：

#include <iostream>
#include <algorithm>
#include <cstdio>

typedef long long LL;

using namespace std;

const int N = 510, mod = 1e9+7;

int n, k;
char g[N][N];
int p[N*N], s[N*N];
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
//快速幂，求逆元，用于分数取模
LL quick_pow(int a, int b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = (res * a) % mod;
        b >>= 1;
        a = (LL)a * a % mod;
    }
    return res;
}
//并查集操作
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
//并查集合并操作
void merge(int x, int y)
{
    int fx = find(x), fy = find(y);
    if(fx != fy) p[fx] = fy, s[fy] += s[fx];
    
}

int main()
{
    cin >> n;
    //下标从1开始，因为需要映射坐标到数字：x * n + y
    for(int i = 1; i <= n; i++) cin >> g[i]+1;
    n++;//映射的数最大为：n*n+n > n^2, n+1后映射最大为n*(n+1)+n < (n+1)^2
    //初始化并查集
    for(int i = 1; i <= n*n; i++)
    {
        p[i] = i;
        s[i] = 1;
    }
    //遍历整个矩阵，将'1'的连通块通过并查集合并
    for(int i = 1; i < n; i++)
        for(int j = 1; j < n; j++)
            if(g[i][j] == '1')
            {
                if(g[i+1][j] == '1') merge(i*n+j, (i+1)*n + j);
                if(g[i-1][j] == '1') merge(i*n+j, (i-1)*n + j);
                if(g[i][j+1] == '1') merge(i*n+j, i*n + j + 1);
                if(g[i][j-1] == '1') merge(i*n+j, i*n + j - 1);
            }
    //遍历并查集，计算初始答案，并记录初始连通块数量cnt
    int cnt = 0;
    LL ans = 1;
    for(int i = 1; i < n; i++)
        for(int j = 1; j < n; j++)
            if(p[i*n+j] == i*n+j && g[i][j] == '1')
            {
                cnt++;
                ans = (ans * s[i*n+j]) % mod;
            }
    for(int i = 1; i <= cnt; i++) ans = (ans * i) % mod;
    //处理每个询问
    cin >> k;
    while(k--)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        x++, y++;//坐标相应+1
        //如果当前更改的位置已经为'1'则直接输出答案
        if(g[x][y] == '1')
        {
            cout << ans << endl;
            continue;
        }
        //当前位置不是'1'，变为1，假设是单独的连通块，先更新答案
        g[x][y] = '1';
        cnt++;
        ans = (ans * cnt) % mod;
        //遍历与当前位置连通的4个位置
        for(int i = 0; i < 4; i++)
        {
            int xx = x + dx[i], yy = y + dy[i];
            int f1 = find(x * n + y);
            //如果是'1'，且在并查集中不在同一个连通块中，更新答案，并将其连通
            if(g[xx][yy] == '1')
            {
                int f2 = find(xx * n + yy);
                if(f1 != f2)
                {
                    ans = ans * quick_pow(cnt, mod-2) % mod;
                    ans = ans * quick_pow(s[f1], mod-2) % mod;
                    ans = ans * quick_pow(s[f2], mod-2) % mod;
                    ans = ans * (s[f1] + s[f2]) % mod;
                    merge(f1, f2);
                    cnt--;
                }
            }
        }
        printf("%lld\n", ans);
    }
    
    return 0;
}

E、三棱锥之刻

题目链接：E.三棱锥之刻

相关：立体几何

因为是正三棱锥，所以求出1面的面积，乘4即可

对一个面：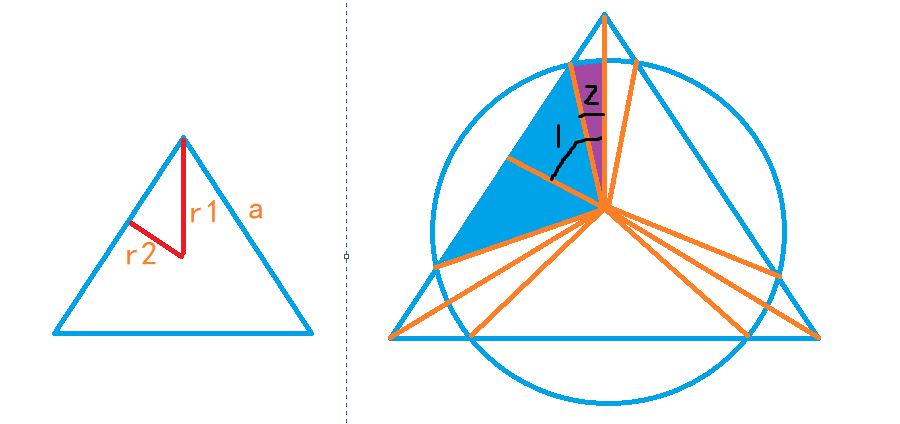

首先计算几个要用到的数据：

1. 中心到面的距离$ h = \sqrt[2]{6} * a / 12$
2. $ r1 = (a * cos30^\circ) / 2 = \sqrt[2]{3} * a / 3$
3. \(r2 = r1 / 2 = \sqrt[2]{3} * a / 6\)
4. 从中心可以够着的区域（圆）的半径$ R = \sqrt[2]{r^2 - h^2}$

分四种情况：

1. 当$ r \leq h$ 时：无法够到四个面，面积为0

2. 当\(r \geq h 且 R \leq r2\)时：够着的区域为三角形内部的整圆，\(s = \pi * R^2 = \pi * \sqrt[2]{r^2 - h^2}\)

3. 当\(R \geq r1\)时：所有区域都能够着，\(s = a^2 * \sqrt[2]{3} / 4\)

4. 当\(r2 < R < r1\)时：够着的区域为3个图中的蓝色三角形+6个图中的紫色扇形

   $ ssan(三角形面积) = 底边*(r2) /2 = r2 * \sqrt[2]{r^2 - h^2 - (r2)^2}$

   \(angle(扇形弧度) = \pi / 3 - acos((r2) / R)\)

   \(sshan(扇形面积) = l*R / 2 = angle * R^2 /2\)

   \(s = 3 * ssan + 6 * sshan\)

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;

const double pi = 3.1415926;

double a, r, h, r1, r2, R;

int main()
{
    cin >> a >> r;
    h = a * sqrt(6) / 12.0;
    r1 = a * sqrt(3) / 3.0;
    r2 = a * sqrt(3) / 6.0;
    R = sqrt(r * r - h * h);
    
    if(r <= h) cout << 0 << endl;
    else if(r > h && R <= r2)
    {
        double s = pi * (r * r - h * h);
        printf("%.5lf\n", 4 * s);
    }
    else if(R >= r1)
    {
        double s = sqrt(3) * a * a / 4;
        printf("%.5lf\n", 4 * s);
    }
    else
    {
        double ssan = sqrt(r*r - h*h - r2*r2) * r2;
        double angle = pi / 3 - acos(r2 / R);
        double sshan = angle * R * R / 2.0;
        double s = 3 * ssan + 6 * sshan;
        printf("%.5lf\n", 4 * s);
    }
    
    return 0;
}

F、对答案一时爽

题目链接：F.对答案一时爽

相关：签到题

分析题意可得：两人均全错时分数最低为：0，当一人全对时最高分为：n + same

代码：

#include <iostream>

using namespace std;

const int N = 110;
int n, same;
char a[N], b[N];

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++) cin >> a[i];
    for(int i = 0; i < n; i++) cin >> b[i];
    for(int i = 0; i < n; i++) if(a[i] == b[i]) same++;
    cout << n + same << ' ' << 0 << endl;
    
    return 0;
}

G、好玩的数字游戏

题目链接：G.好玩的数字游戏

相关：大模拟

待补。。。。。。

H、幂塔个位数的计算

题目链接：H.幂塔个位数的计算

参考题解：https://blog.nowcoder.net/n/d4fef62909f2421890d32c00d1403c0c

相关：找规律

写数据找规律：

对a^i:枚举a的不同个位数对不同i的结果的个位数
0:{0} 0 0 ......              5:{5} 5 5 ......
1:{1} 1 1 ......              6:{6} 6 6 ......
2:{2 4 8 6} 2 4 8 6 ......    7:{7 9 3 1} 7 9 3 1 ......
3:{3 9 7 1} 3 9 7 1 ......    8:{8 4 2 6} 8 4 2 6 ......
4:{4 6} 4 6 ......            9:{9 1} 9 1 ......

• 对a的个位数是2的，循环节为4

  对\(a^a\): 若\(a\%4 == 2\) —— 4；若\(a\%4 == 0\) —— 6；

  对\(a^{a^a}\): 因为\(a = 10x+2\),为偶数，偶数个2相乘 % 4 == 偶数个0相乘 % 4== 0 —— 6。

• 对a的个位数是8的，循环节为4

  对\(a^a\): 若\(a\%4 == 2\) —— 4；若\(a\%4 == 0\) —— 6；

  对\(a^{a^a}\): 因为\(a = 10x+8\),为偶数，偶数个2相乘 % 4 == 偶数个0相乘 % 4 == 0 —— 6。

• 对a的个位数是的3，循环节为4

  对\(a^a\): 若\(a\%4 == 3\) —— 7；若\(a\%4 == 1\) —— 3；

  对\(a^{a^a}\): 因为\(a = 10x+3\),为奇数，奇数个3相乘 % 4 == 3——7，偶数个1相乘 % 4 == 1 —— 3。

• 对a的个位数是的7，循环节为4

  对\(a^a\): 若\(a\%4 == 3\) —— 3；若\(a\%4 == 1\) —— 7；

  对\(a^{a^a}\): 因为$a = 10x+$7,为奇数，奇数个3相乘 % 4 == 3——3，偶数个1相乘 % 4 == 1 —— 7。

• 对a的个位数是的4，循环节为2

  对\(a^a\): 若\(a\%2 == 0\) —— 6；

  对\(a^{a^a}\): 因为\(a = 10x+4\),为偶数，偶数个0相乘 % 2 == 0——6。

• 对a的个位数是的9，循环节为2

  对\(a^a\): 若$a%2 == $1 —— 9；

  对\(a^{a^a}\): 因为\(a = 10x+9\),为奇数，奇数个1相乘 % 2 == 1——9。

综上所述：

对a的个位数是0、1、5、6、9的，幂塔个位数都为a本身的个位数
对a的个位数是4的。幂塔个位数均为6
对a的个位数是2、8的，若幂塔层数为2，则由a%4的结果决定(0-6, 2-4);若层数大于2，则个位数均为6
对a的个位数是3的，无论幂塔层数，个位数仅由a%4的结果决定(3-7, 1-3)
对a的个位数是3的，无论幂塔层数，个位数仅由a%4的结果决定(3-3, 1-7)

代码：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5+10;

char s1[N], s2[N];

int main()
{
    cin >> s1+1 >> s2+1;
    s1[0] = '0', s2[0] = '0';
    int l1 = strlen(s1), l2 = strlen(s2);
    //a:个位数
    int a = s1[l1 - 1] - '0';
    //b:a%4
    int b = ((s1[l1 - 2] - '0') * 10 + (s1[l1 - 1] - '0')) % 4; 
    int n = s2[l2 - 1] - '0';
    //当n == 1的时候，直接输出a，记得结束程序
    if(l2 == 2 && n == 1) {cout << a << endl; return 0;}
    if(a == 0 || a == 1 || a == 5 || a == 6 || a == 9) cout << a << endl;
    if(a == 4) cout << 6 << endl;
    if(a == 2 || a == 8)
        if(l2 == 2 && n == 2 && b) cout << 4 << endl; //n==2且a%4==2时
        else cout << 6 << endl;
    if(a == 3)
        if(b == 1) cout << 3 << endl;//a%4 == 1时
        else cout << 7 << endl;
    if(a == 7)
        if(b == 1) cout << 7 << endl;//a%4 == 1时
        else cout << 3 << endl;
    
    return 0;
}

I、限制不互素对的排列

题目链接：I.限制不互素对的排列

相关：找规律、构造

由题意可得出的性质：

1. 当所有偶数连续排列时，可以构成含n/2 - 1对相邻且gcd > 1的排列
2. 要求最大值为n/2对，而满足gcd(奇数，偶数) > 1的最小数对为（6， 3），故可将6放置偶数末尾，当对数不够时再将3放置在6后面
3. 将剩余的数从大到小依次排列即可
4. 由2可导出：当n < 6 && (n / 2 - 1) < k时，无法构造

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int n, k;
bool st[N];

int main()
{
    cin >> n >> k;
    if(n < 6 && n / 2 - 1 < k) cout << -1 << endl;
    else
    {
        int i = 2, j = 0;
        for(i = 2, j = 0; i <= n && j <= k; i += 2) 
            if(i != 6) 
            {
                printf("%d ", i);
                st[i] = true;
                j++;
            }

        if(j < k + 1)
        {
            printf("6 ");
            st[6] = true;
            j++;
        }
        
        if(j < k + 1) 
        {
            printf("3 ");
            st[3] = true;
        }
        int t = 1;
        while(t <= n) if(!st[t++]) printf("%d ", t-1);
    }
    
    return 0;
}

J、一群小青蛙呱嘣呱嘣呱

题目链接：J.一群小青蛙呱嘣呱嘣呱

题解参考：https://blog.nowcoder.net/n/96ba5fe158194f0a8e37bd6e767ee0e2

相关：线性筛法、最小公倍数、快速幂

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <math.h>

typedef long long LL;

using namespace std;

const int N = 2e8+10, mod = 1e9+7;

int n;
int primes[N], cnt;
bool st[N];

LL quick_pow(int a, int b)
{
    LL ans = 1;
    while(b)
    {
        if(b & 1) ans = ans * a % mod;
        b >>= 1;
        a = (LL)a * a % mod;
    }
    
    return ans;
}

int main()
{
    cin >> n;
    LL ans = 1;
    
    for(int i = 2; i <= n / 2; i++)
    {
        if(!st[i]) 
        {
            primes[cnt++] = i;
            if(i == 2) ans = (ans * quick_pow(2, floor(log(n/3) / log(2)))) % mod;
            else ans = (ans * quick_pow(i, floor(log(n/2) / log(i)))) % mod;
        }

        for(int j = 0; primes[j] <= n / (2 * i); j++)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
    
    if(ans == 1) puts("empty");
    else cout << ans << endl;
    
    return 0;
}