基础算法
大纲
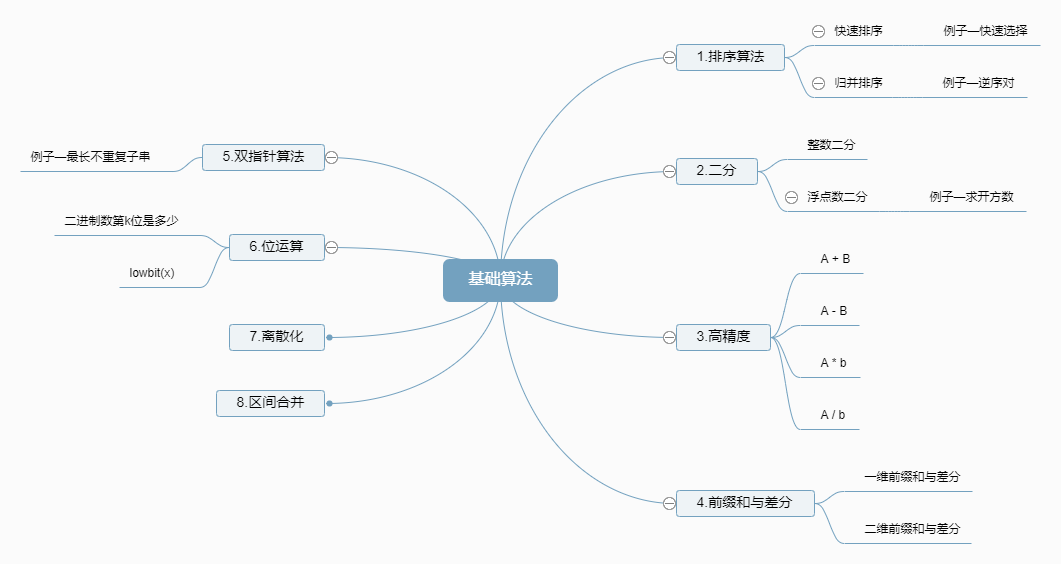
一、排序
1、快速排序
//模板, 时间复杂度 O(nlogn)
//特别注意边界问题和基准点的选取
//x = q[l] 时,递归不能用 i - 1
//x = q[r] 时,递归不能用 j + 1
//一般情况下,右边界、左边界、随机点均可,但是对已经排好序的数列,取边界点会导致最坏情况,复杂度达到 O(n^2)
//所以最佳做法是取随机数,中点也不是最佳取法
//边界问题想不清楚
void quick_sort(int q[], int l, int r)
{
if(l >= r) return;
int x = q[l + r >> 1], i = l - 1, j = r + 1;
while(i < j)
{
while(q[++i] < x);
while(q[--j] > x);
if(i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
2、归并排序
//模板
void merge_sort(int q[], int l, int r)
{
if(l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while(i <= mid && j <= r)
{
if(q[i] <= q[j]) temp[k++] = q[i++];
else temp[k++] = q[j++];
}
while(i <= mid) temp[k++] = q[i++];
while(j <= r) temp[k++] = q[j++];
for(i = l, j = 0; i <= r; i++, j++) q[i] = temp[j];
}
二、二分
1、整数二分
//模板
bool check(int x)
{
/*检查x是否满足某种性质*/
}
//区间[l, r]被划分为[l, mid] 和 [mid + 1, r] 时
int bsearch_1(int l, int r)
{
while(l < r)
{
int mid = l + r >> 1;
if(check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
//区间[l, r]被划分为[l, mid - 1] 和 [mid, r] 时
//当 l 被更新为 mid 时, mid = l + r + 1 >> 1, 如果不 +1,mid会永远被更新为l
int bsearch_2(int l, int r)
{
while(l < r)
{
int mid = l + r + 1 >> 1;
if(check(x)) l = mid;
else r = mid - 1;
}
return l;
}
2、浮点数二分
//模板
bool check(double x)
{
/*检查x是否满足某种性质*/
}
const double eps = 1e-6;// eps表示精度,一般题目要求小数点后i位, 精度就定位1e(-i-2)
double bsearch(double l, double r)
{
while(r - l > eps)
{
double mid = (l + r) / 2;
if(check(x)) r = mid;
else l = mid;
}
return l;
}
三、高精度
1、大数 + 大数
//引用减少拷贝时间,加快速度
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t = 0;
for(int i = 0; i < A.size() || i < B.size(); i++)
{
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10; //进位
}
if(t) C.push_back(1);
return C;
}
string a, b;
vector<int> A, B;
//逆序
for(int i = a.size()-1; i >= 0; i--) A.push_back(a[i] - '0');
for(int i = b.size()-1; i >= 0; i--) B.push_back(b[i] - '0');
vector<int> C = add(A, B);
//逆序输出
for(int i = C.size()-1; i >=0; i--) printf("%d", C[i]);
//压9位,模板
const int base = 1000000000;
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t = 0;
for(int i = 0; i < A.size() || i < B.size(); i++)
{
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % base);
t /= base;
}
if(t) C.push_back(t);
return C;
}
string a, b;
vector<int> A, B;
cin >> a >> b;
//s:存储压位的每一个数,j:记录位数,t:记录乘的10
for(int i = a.size()-1, s = 0, j = 0, t = 1; i >= 0; i--)
{
s += (a[i] - '0') * t;
j++, t *= 10;
if(j == 9 || i == 0)
{
A.push_back(s);
s = j = 0;
t = 1;
}
}
for(int i = b.size()-1, s = 0, j = 0, t = 1; i >= 0; i--)
{
s += (b[i] - '0') * t;
j++, t *= 10;
if(j == 9 || i == 0)
{
B.push_back(s);
s = j = 0;
t = 1;
}
}
vector<int> C = add(A, B);
cout << C.back();
for(int i = C.size()-2; i >= 0; i--) printf("%09d", C[i]);
2、大数 - 大数
//模板A-B
//判断两数的大小
bool cmp(vector<int> &A, vector<int> &B)
{
if(A.size() != B.size()) return A.size() > B.size();
for(int i = A.size() - 1; i >= 0; i--)
if(A[i] != B[i]) return A[i] > B[i];
return true;
}
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
//t是借位
for(int i = 0, t = 0; i < A.size(); i++)
{
t = A[i] - t;
if(i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if(t < 0) t = 1;
else t = 0;
}
//去前导0
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
string a, b;
vector<int> A, B;
cin >> a >> b;
//逆序
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
//比较
if(cmp(A, B))
{
vector<int> C = sub(A, B);
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
}
else
{
vector<int> C = sub(B, A);
putchar('-');
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
}
3、大数 * 小数
//模板A * b
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
for(int i = 0, t = 0; i < A.size() || t; i++)
{
if(i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
//去前导0
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
string a;
int b;
vector<int> A;
cin >> a >> b;
//逆序
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
vector<int> C = mul(A, b);
//逆序输出
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
4、大数 / 小数
//模板A / b
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for(int i = A.size() - 1; i >= 0; i--)
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b; //余数
}
//C已经是正确结果,但是为了保证加减乘除的一致性和去掉前导0,需要逆序
reverse(C.begin(), C.end());
//去前导0
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
string a;
int b;
vector<int> A;
cin >> a >> b;
//逆序
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
int r;
vector<int> C = div(A, b, r);
//逆序输出
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
cout << '\n' << r << endl;
四、前缀和与差分
1、一维前缀和与差分
//一维前缀和
//S[i] = a[1] + a[2] + ... a[i]
//a[l] + ... + a[r] = S[r] - S[l - 1]
int n;
int a[N], s[N];
//初始化前缀和
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i++) s[i] = s[i-1] + a[i];
//求某个区间和
int l, r;
scanf("%d%d", &l, &r);
printf("%d", s[r] - s[l-1]);
// 一维差分
//给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
//假设原数组a[]为前缀和,b[]为a[]数组差分数组
//让差分数组b[]的某一个+C, a[]的后一段全+c
int n, m;
//a[] 叫 b[]的前缀和, b[] 叫 a[] 的差分
int a[N], b[N];
void insert(int l, int r, int c)
{
b[l] += c;
b[r + 1] -= c;
}
//输入原数组,同时初始化差分数组
for(int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
insert(i, i, a[i]);
}
//对一个区间内的数批量+c
while(m--)
{
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
//利用差分数组求更改后的数组(差分求前缀和)
for(int i = 1; i <= n; i++) b[i] += b[i-1];
for(int i = 1; i <= n; i++) printf("%d ", b[i]);
// for(int i = 1; i <= n; i++) a[i] = a[i-1] + b[i];
// for(int i = 1; i <= n; i++) printf("%d ", a[i]);
2、二维前缀和与差分
//二维前缀和
//S[i, j] = 第i行j列格子左上部分所有元素的和
//以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
//S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
int n, m;
int a[N][N], s[N][N];
//初始化前缀和
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
//求某个子矩阵的和
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
//二维差分
//给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
//S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x1][y2+1] -= c;
b[x2+1][y1] -= c;
b[x2+1][y2+1] += c;
}
//初始化差分矩阵
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
insert(i, j, i, j, a[i][j]);
}
//对某个子矩阵全+c
while(q--)
{
int x1, y1, x2, y2, c;
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
insert(x1, y1, x2, y2, c);
}
//对差分矩阵求前缀和,得到原矩阵
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
b[i][j] += b[i][j-1] + b[i-1][j] - b[i-1][j-1];
printf("%d ", b[i][j]);
}
puts("");
}
五、双指针算法
//利用i,j的某种规律,把暴力的嵌套循环(O(n^2)复杂度)优化为O(n).
for (int i = 0, j = 0; i < n; i ++ )
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
/*常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作*/
六、位运算
lowbit(x)证明:
//n 二进制中第k为位是几
n >> k & 1
//lowbit(x) : 返回x的最后一位1
//如: n = 10 = 1010 , 则 lowbit(n) = 10(二进制) = 2
return x & -x
/*基本应用:
1、x二进制中1的个数
2、树状数组 */
//x二进制中1的个数
while(x) x -= lowbit(x), ans++;
七、离散化
1、把所有“大值数字”(实际位置值)存入 alls,因为下标是唯一的,所以在排序的同时要去重;
2、 离散化操作:
因为:对alls中的位置值已经排好序,
所以:可以用二分把alls中存的 “ 实际位置值 ” 映射到 “ alls中的下标 ”, 并赋值给x
a[x] += C, 其中x满足alls[x] = 实际位置值
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}

八、区间合并
//将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
vector<PII> res;
//按左端点排序
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;
for(auto seg : segs)
if(ed < seg.first)
{
if(st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
else ed = max(ed, seg.second);
if(st != -2e9) res.push_back({st, ed});
segs = res;
}
基础算法(提高)
一、位运算——龟速乘
题目链接 :90. 64位整数乘法
类比快速幂,将大数乘法转换成加法
LL qadd(LL a, LL b, LL p)
{
LL res = 0;
while(b)
{
if(b & 1) res = (res + a) % p;
a = (a + a) % p;
b >>= 1;
}
return res;
}
二、环形均分问题(排序、中位数)
题目链接:
描述:n个人围成一圈,每个人手中有若干物品,可以向相邻的人传递物品,求至少需要传递多少个物品能够是每个人的物品数量都相等。
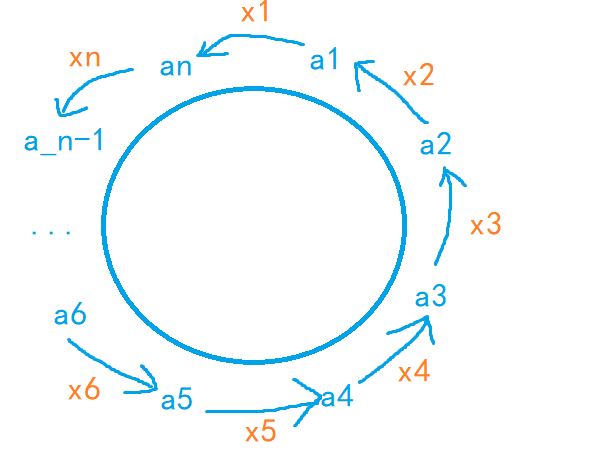
首先,要求传递最少,则不会出现两人相互传递的情况。设像上图那样单项传递(注意:\(x_i\)可正可负)。
则问题转化为求\(|x_1| +|x_2| + ... + |x_n|\)的最小值
设平均值为$ a = (a_1 + a_2 + ... + a_n) / n$(若a不为整数,显然无法操作),则可以得出:
\(\left\{\begin{aligned} a_1 - x_1 + x_2 =& a \\ a_2 - x_2 + x_3 =& a \\ ...& \\ a_{n-1} - x_{n-1} + x_n =& a \\ a_n - x_n + x_1 =& a \end{aligned}\right.\) \(\Longrightarrow\) \(\left\{\begin{aligned} x_1 - x_2 =& a_1 - a \\ x_2 - x_3 =& a_2 - a \\ ...& \\ x_{n-1} - x_n =& a_{n-1} - a \\ x_n - x_1 =& a_n - a \end{aligned}\right.\) $ \Longrightarrow$ \(\left\{\begin{aligned} x_1 =& x_1 - 0 \\ x_2 =& x_1 - (a_1 - a) \\ x_3 =& x_1 - (a_1 + a_2 - 2a) \\...& \\ x_n =& x_1 - (a_1 + a_2 + ... + a_{n - 1} - (n-1)a) \end{aligned}\right.\)
将\(x_1\)后面减的常数依次设为\(C_1 \sim C_n\) 。
则\(\begin{aligned} &|x_1| +|x_2| + ... + |x_n| \\ =&|x_1 - C_1| + |x_1 - C_2| + ... + |x_1 - C_n| \\ \Rightarrow &数轴上选一点,求其到各点C_i的距离和最小 \\ \Rightarrow &求中位数 \end{aligned}\)
三、对顶堆求动态中位数
题目链接:106. 动态中位数
描述:给一个数组,不断向其中添加数字,如果添加后的总数为奇数,则输出中位数。
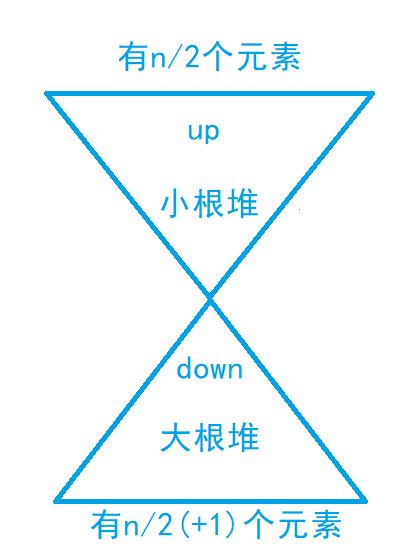
满足条件:
- up堆的所有元素都大于等于down堆的所有元素
- down元素个数最多比up堆多1个
down堆的堆顶元素即为中位数
四、RMQ
题目链接:1273. 天才的记忆
解决问题:求区间最值问题
思想:倍增、动态规划
状态表示:f[i][j] : 表示从i开始,长度为2^j的区间最值
状态转移:f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1])
以最大值为例:
void init()
{
for(int j = 0; j < M; j++)
for(int i = 0; i + (1 << j) - 1 <= n; i++)
if(!j) f[i][j] = a[i];
else f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
查询操作:设k为满足\(2^k \leq len\)的最大值,则被查询区间可以被划分为f[l][k] 和 f[r - (1 << k) + 1][k]
int query(int l, int r)
{
int len = r - l + 1;
int k = log(len) / log(2);
return max(f[i][k], f[r - (1 << k) + 1][k]);
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号