地层压力预测软件设计与实现

1. 概述

估算或预测地层压力，特别是超压地层的压力预测，对于油气勘探开发各个环节都具有非常重要的影响：在勘探阶段地层压力场的预测有助于评价盖层的有效性，描述油气运移路径，有利于分析圈闭的几何形状并为盆地模拟提供校正；地层压力的准确预测．能够为后期井壁稳定性分析、不同层位井段的钻井液密度确定、井身结构优化及套管层数和下人深度的确定提供科学依据。开发阶段，地层压力场预测结果有助于确定储层的驱动和连通情况。

 

引用标准：SY/T 5623—2009 中华人民共和国石油天然气行业标准——地层压力预（监）测方法，2010

2. 理论基础

2.1. 压力的基本概念

静液压力：由液柱自身的重力所引起的压力。液柱的大小和形状对压力的大小没有影响[]。

 

其中 Ph——静液压力

ρ——平均密度

g——重力加速度

D——液柱高度

就钻井作业而言，可以写成：

 

其中 D——液柱垂直高度，ft

MW——流体或钻井液密度，lb/gal (ppg)或lb/ft3

C——转换常数（当MW单位为lb/gal时C=0.052，MW单位为lb/ft3时C=0.00695）。

上覆岩层压力：地层某处以上地层岩石基质和岩石孔隙中流体总重力所产生的压力。

 

其中 D——地层深度，ft

ɸ——地层孔隙度，小数

ρma——岩石骨架密度，lb/ft3

ρfl——流体密度，lb/ft3

地层压力：作用于地层孔隙空间中流体（地层水、油、气）的压力。

任何地质环境中的正常地层压力都将等于水从地表到地下地层的静水压头（即静水压）。根据定义，异常地层压力以偏离正常趋势线为特征，在特定地质环境中超过静水压力（Pr>PHy）的地层压力被定义为异常高压（超压），而低于静水压力的地层压力称为异常低压（欠压）。全球油气资源勘探（包括陆上和海上）表明，世界各地都存在异常地层压力，超压比欠压发生得更频繁。

 

其中 Po——上覆岩石压力（总垂直应力、岩石静压力）

Pt——地层压力（孔隙流体压力、孔隙压力）

δ——颗粒间压力（基质应力、有效应力、垂直岩石框架应力）

地层破裂压力：在井下一定深度的地层，承受流体压力的能力达到一定数值时会使地层破裂，这个液体压力称为地层破裂压力。

2.2. 压力异常原因

产生异常高地层压力（AHFP）的机制类型[]

  • 岩石孔隙体积的变化
    • 欠压实作用（垂直荷载）
    • 构造挤压（侧向构造荷载）
    • 二次胶结
  • 间质液体体积的变化
    • 温度变化（水热膨胀）
    • 矿物转化
    • 生烃
    • 碳氢化合物分解（产热）
    • 流体迁移
  • 流体压力的变化（液压头）即流体运动
    • 透析
    • 流体压力头
    • 油田生产作业
    • 冻土环境
    • 油气比重差异

 

产生异常低地层压力（ALFP）的机制类型

  • 岩石孔隙体积的变化
    • 岩石扩容
    • 构造运动
    • 孔隙体积增加
  • 间质液体体积的变化
    • 温度变化
  • 流体压力的变化（液压头）即流体运动
    • 透析
    • 液体（气体、油和/或水）的生产
    • 气体迁移
    • 地下水运动

2.3. 孔隙度计算

孔隙水随着埋深的增加和温度的升高而膨胀，而孔隙空间则随着静载荷的增加而减小。因此，只有在存在足够渗透率的路径以允许地层水容易逸出的情况下，才能维持正常的地层压力。只要孔隙水能够按照自然压实速率的要求迅速逸出，孔隙压力就会保持在静水压力下。然而，如果水流路径被堵塞或严重限制，增加的上覆应力将导致孔隙水加压超过静水压力。对于给定的埋深，孔隙体积也将保持大于正常值。由于细粒沉积物（如页岩或蒸发物）的压实而导致的渗透性的正常损失，可能会形成一种密封，从而产生异常压力。给定深度的体积密度与骨架密度、孔隙流体密度和孔隙度有关。

 

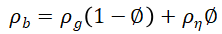
体积密度随埋深的变化主要与压实作用下沉积物孔隙度的变化有关。沉积矿床中常见矿物的体积密度变化不大，通常可以假定为具有代表性的平均值（孔隙流体密度也是如此）。孔隙度可用方程中的平均体积密度表示。

 

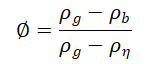
该方程使得从测井曲线中读取的平均体积密度数据可以很容易地表示为任何假定骨架密度和流体密度的平均孔隙度。如果在半对数纸上绘制这些平均孔隙度值与深度的关系曲线，通常可以获得良好的直线趋势。这条线的方程式如下：

 

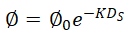
式中，f为表层孔隙度，K为孔隙度衰减常数，为沉积岩离地表下面的深度。

2.4. 估算孔隙压力的方法

大多数异常地层压力的检测和估算方法都是基于这样一个事实，即在同一埋深下，异常压力的地层往往比正常压力的类似地层压实程度低，孔隙度高。因此，任何反映地层孔隙度变化的测量方法也可用于检测异常压力。通常，所测定的孔隙度相关的参数都会绘制成随深度变化的曲线。

如果地层压力是正常的，孔隙度的相关参数应具有易于识别的趋势（“正常趋势”），因为孔隙度随着埋深和压实的增加而降低。偏离正常压力趋势表明可能转变为异常压力的过渡区。异常压力区的上部通常称为过渡带。检测发生这种偏离的深度至关重要，因为必须在井内设置套管，然后才能安全地钻穿异常高压渗透层。

根据孔隙度参数随深度变化的曲线，有两种方法来定量预测地层压力。第一种方法是基于假设具有相同孔隙度参数的地层具有相同的有效的岩石骨架应力基础上。因此，异常压力地层在特定深度处的骨架应力状态与较浅正常压力地层的骨架应力状态相同。然而，由于压实历史和地质条件的变化，不同地层带之间没有一致的正常趋势。

第二种方法是通过孔隙度与深度曲线建立经验关系式计算地层压力。经验关系式法通常被认为比第一种计算方法更准确。经验关系式法的困难在于，在建立经验相关性之前，必须有大量的相关数据。

异常地层压力的探测和估算技术可分为：（1）预测方法；（2）随钻使用的方法；（3）测试方法。最初的野猫井规划必须包含通过预测方法获得的地层压力信息。在钻井作业期间更新初始估计值，在钻完目标层段后，在下套管前应用各种地层评价方法再次检查地层压力。

钻井前对地层孔隙压力的估计主要基于（1）邻井可用数据的相关性分析和（2）地震数据。

3. 解决方法

3.1. 体积密度法

钻井时对地层岩石碎片的连续评估可以提供有关地下地层的有价值的信息。如果以前钻井的数据可用，可用于估计在同一附近钻井的新井的地层孔隙压力，这些新井可能遇到相同或类似的地层。岩屑体积密度可通过多种技术获得，包括（1）水银泵、（2）泥浆天平或（3）可变密度液柱。无论采用哪种技术，最终结果都将是整个井内页岩岩屑的近似体积密度值。

页岩密度是一个与孔隙度相关的参数，通常绘制其与深度的关系图来估计地层压力。当由纯页岩组成的岩屑的体积密度显著低于页岩的正常压力趋势线时，表明压力异常。确定地层压力的一种方法是利用一条经验换算曲线，称为Boatman，其中地层压力梯度（psi/ft）与页岩密度差（r）（以g/cm3为单位）绘制。用指数孔隙率表达式代替指数孔隙率表达式，建立了泥质岩屑体积密度的正态压实趋势数学模型

 

 

 

 

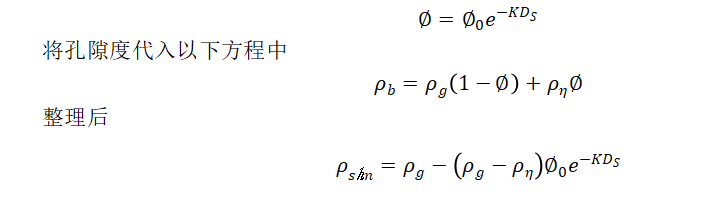
其中是正常压力页岩的页岩密度。纯页岩体积密度为2.65。平均孔隙流体密度可从表2-1中找到，常数和K可基于在正常压力地层中进行的页岩岩屑体积密度测量。在实际应用中，通过直观地提取正常趋势，并用数学方法进行外推和K，得到目标深度下岩屑密度的“正常值”。然后，根据预期的正常密度计算页岩密度差，从Boatman相关性中获得异常压力读数。

 

表2-1 几个重点钻井地区的正常地层压力梯度

地区

压力梯度

Psi/ft

地层水当量密度

Kg/m3

德克萨斯州西部

0.433

1,000

墨西哥湾沿岸

0.465

1,074

北海

0.452

1,044

马拉西亚

0.442

1,021

马更些河三角洲

0.442

1,021

西非

0.442

1,021

埃拉达克盆地

0.433

1,000

落基山脉

0.436

1,007

加利福尼亚

0.438

1,014

 

 

3.2. 修正d指数法

当钻井进入正常地层压力和异常地层压力的过渡区时，岩石性质和钻头性能的变化往往提供了地层压力变化的许多间接指示。为了检测这些变化，对与钻头性能有关的钻井参数进行连续监测，并由地面仪器记录。此外，还监测与钻井液相关的许多变量以及从油井中循环的岩屑。

如果井筒压力降到渗透性地层的孔隙压力以下，这可能导致井涌和地层流体流入井内。在这种情况下，当开始井控作业时，关井钻杆压力将提供直接和准确的地层压力指示。

钻头性能的变化可以通过在地面进行的测量来检测，最常见的测量参数包括（1）钻速、（2）悬重、（3）转速和（4）扭矩。钻井液的性能参数也会受到监测，因为这会对渗透率产生影响。钻头的钻速通常随地层类型的不同而发生显著变化，一般来说，在给定的地层类型中，钻头的钻速随深度的增加而降低。然而，当遇到异常压力的过渡区时，这种正常趋势就会改变。在地层孔隙压力梯度较高的过渡带上方，经常会遇到坚硬的、通常为灰色的地层，这将以低于正常的钻井速度进行钻井。认为这些地层为极低渗透地层，对异常压力梯度形成压力封闭。这些密封层的厚度从几英尺到几百英尺不等。在异常压力盖层下方，正常渗透率趋势逆转，渗透率随深度增加。

除地层类型和地层孔隙压力外，许多钻井变量都会影响钻速，其中一些附加参数包括（1）钻头类型，（2）钻头尺寸，（3）钻头喷嘴尺寸，（4）钻头磨损，（5）钻头重量，（6）转速，（7）泥浆类型，（8）泥浆密度，（9）有效泥浆粘度，（10）泥浆中的固体含量和粒度分布，（11）泵压，（12）泵速。影响渗透率的变量的变化有时屏蔽改变岩性或增加地层孔隙压力的影响。因此，仅使用渗透率数据往往难以检测地层压力变化，在预测地层压力时，应结合使用其他指标。

当使用磨齿钻头时，磨齿磨损的影响会影响钻头每次运行时的钻速。当其他钻井变量不变时，通过建立正常压力地层中过去钻头性能的预期正常趋势，可以部分补偿钻头钝化的影响。在某些情况下，由于齿面磨损，过渡区的穿透率将随着深度的增加而降低，但降低的速度远低于预期。其他钻井变量的变化可能会导致类似的影响，并被误解为压力增加。特别是钻头类型的变化使得从渗透率数据中很难检测到孔隙压力的变化。

提出了旋转钻井过程的经验模型，用以数学补偿影响钻速的更重要变量变化的影响。Bingham和Bourgoyne发表了第一批经验模型。对于重量变化对钻头W、转速N和钻头直径db的影响，前一种模型通过计算由定义的d指数来归一化钻速R

 

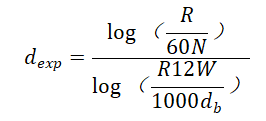
其中测量单位为R–ft/hr、N–rpm、W–k-lbf和db–in。

在钻井液密度不变的情况下，d指数方程可以用来检测正常压力向异常压力的转变。这项技术涉及绘制在给定类型的低渗透地层中获得的d随深度的函数。页岩几乎总是选择的地层类型，在其他地层类型中获得的钻井数据可以简单地从计算中省略。在正常压力地层中，d指数随深度的增加而增加，但在遇到异常压力地层后，d指数随深度的增加不太快，从而偏离了正常压力趋势。在许多情况下，会发生完全的趋势逆转，而d指数实际上会随着深度而减小。

1971年，Rehm和McClendon提出修改d指数，以校正泥浆密度变化以及重量变化对钻头、钻头直径和转速的影响。这个修正的d指数是用

  

 

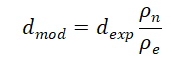
式中，r是相当于正常地层孔隙压力梯度的泥浆密度，r是循环时钻头处的当量泥浆密度。

修正的d指数常用于地层孔隙压力梯度的定量估计和异常地层压力的定性检测。除了等效基体应力概念外，还发展了许多经验关联式。

Rehm和McClendon建议在构建定量估计地层孔隙压力的图表时，对深度和dmod值使用线性标度。假设截距(dmod)0和斜率为m的直线正常压力趋势线.

 

 

 

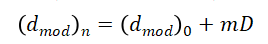
作者认为，随着地质年代的变化，斜率m的值相当恒定（m=0.000038ft-1）。对于dmod图的观测偏差和地层压力梯度gp，给出了以下经验关系式

 

 

 

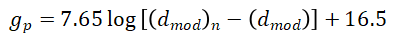
其中(dmod)n是从相关深度处的正常压力趋势线读取的dmod值。在这个方程中，gp用当量泥浆密度单位lbm/gal表示。

Zamora建议在构建定量估计地层孔隙压力的图表时，使用深度的线性刻度，但使用dc值的对数刻度。具有截距(dmod)0和指数m的直线正常压力趋势线如下：

(dmod)n=(dmod)0emD

Zamora报告说，正常压力趋势线的斜率变化很小，与位置或地质年龄无关，m值为0.000039 ft-1。Zamora使用以下经验关系式来表示图中观察到的偏差和地层压力梯度gp。

 

 

 

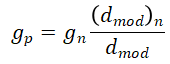
其中gn是该区域的正常压力梯度。

3.3. 电阻率法

测量地层电导率或电阻率（电导率的倒数）的测井设备几乎用于每一口钻井。由于数据几乎总是现成的，因此电导率是测井估计孔隙压力时最常用的孔隙度相关参数。地层系数一词通常是指水饱和地层的电阻率与水的电阻率之比。地层系数也可以用导电率表示。

 

 

地层系数F与孔隙度Ф的关系由经验公式确定

 

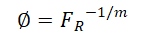
其中，指数m在1.4和3.0之间变化。当实验室数据不可用时，通常在实践中使用平均值2.0。

地层电导率C0或R0随岩性、水矿化度、温度和孔隙度的变化而变化。为避免岩性引起的变化，仅使用在本质上纯页岩中获得的值。由于石灰岩组分对观察到的电导率有很大影响，因此避免了含有一些石灰岩的页岩。在计算地层系数时，可以考虑盐度和温度变化的影响，如果在指定的温度和盐度下有目标深度的水的电导率CW或电阻率RW现场值可以直接使用。

井眼附近的地层电导率或电阻率也受到钻井液暴露的显著影响。尽管页岩地层对泥浆滤液的侵入相对渗透，但钻井液和井壁之间的化学作用通常会导致页岩性质的变化。由高水敏性页岩组成的钻孔剖面在不同时间给出了不同的测井读数。这个问题可以通过使用深度探测半径的测井设备来最小化。

用指数孔隙度方程可以得到泥页岩地层因素的正常压实趋势的数学模型：

 

 

 

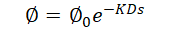
孔隙率

 

 在重新排列项之后，这个替换产生

 

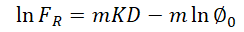
常数和K必须根据在相关区域正常压力地层中获得的电导率数据进行选择。

然而，在实践中，由于水的导电性CW或电阻率RW随深度而变化，且不易获得，因此假设其为常数，则正常压实趋势导电性变为：

 

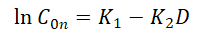
其中，和K2=mK。当然，K1和K2必须通过数据拟合在正常压力地层的电导率/电阻率数据上选择。

根据外推正常趋势的实测电导率/电阻率与“正常电导率/电阻率”之比，使用区域相关关系来计算地层压力。当页岩电导率显著低于外推的正常趋势值时，表明存在异常压力。

Hottman和Johnson提出了可渗透砂岩中测得的地层压力与相邻地层页岩电阻率之间的第一个经验关系，而Matthew和Kelley发表了德克萨斯州南部和路易斯安那州墨西哥湾海岸的类似关系。

3.4. 声波时差法

在规划开发井时，重点放在该地区以往钻井经验的数据上。对于探井，只有地震数据可用。为了从地震资料中估算地层孔隙压力，必须确定作为深度函数的平均声速。为方便起见，通常会显示速度的倒数，或区间通过时间（ITT）。

观察到的ITT（）是一个孔隙度相关参数，根据以下关系随孔隙度变化。

 

 

 

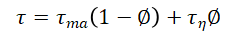
式中，是岩石基质中的ITT，是孔隙流体中的ITT。由于流体的传输时间大于固体的传输时间，岩石中观察到的传输时间随着孔隙度的增加而增加。

在绘制孔隙度相关参数与深度的关系图以估计地层孔隙压力时，最好使用数学模型将正常压力趋势（在浅层沉积物中观察到）外推到地层压力异常的较深深度。通常假设线性、指数或幂律关系，因此可以在笛卡尔、半对数或对数纸上将正常压力趋势绘制为直线。在某些情况下，这些方法中的任何一种都无法观察到可接受的直线趋势，必须使用更复杂的模型。

用指数孔隙度表示式代替ITT法向压实趋势的数学模型如下：

 

 

 

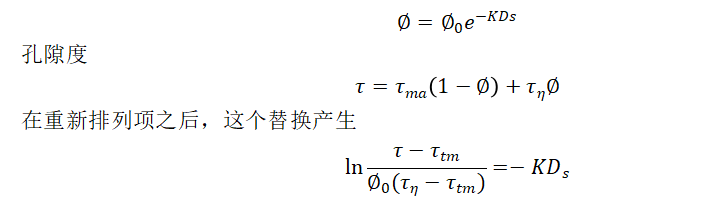
平均观测沉积运移时间与深度D的正压关系因基质运移时间也随孔隙度变化而复杂。这一差异是压实对页岩基质运移时间的影响所致。值在未压实页岩167到高压实页岩的62 之间变化。此外，地层随深度的变化也会引起基质移动时间和正常压实常数和K的变化。如果有足够的正常压力数据，这些问题可以得到解决。

从地震衍生的ITT数据（如Pennebaker方法）估算地层压力的程序与使用测井衍生的ITT数据的程序基本相同。主要区别在于，测井数据仅包括页岩地层数据，而地震数据无法准确确定岩性，因此必须使用所有地层的平均ITT。

页岩沉积物的地质年代已被发现影响ITT和深度之间的正常压力关系。较老的沉积物发生压实的时间较长，导致正常压力趋势线向上移动。同样，较年轻的沉积物导致正常压力趋势线向下移动。

3.5. Pennebaker法

Pennebaker图通常用于根据地震叠加速度数据确定地层孔隙压力。Pennebaker图是深度与地震波速的关系图（表示为间隔传输时间（ITT），单位为微秒/英尺）。Pennebaker假设ITT在正常压实趋势下对深度具有幂律依赖性。对数刻度下，页岩正常速度（传输时间）压实趋势应大致呈直线。页岩中任何偏离正常压实线（或速度变化）的现象都可能是欠压实和超压的迹象。注意，主要的岩性变化也会产生与任何超压无关的大速度变化，该技术应始终利用所有可用的地质知识来定性解释。

根据来自不同地区的大量油井标定，已观察到超压程度与偏离正常基线的速度量成正比。因此，Pennebaker曲线图的主要目的是允许在曲线图上设置正常压力基线，以确定具体深度和速度反转处可能超压的程度。

为方便起见，通常会显示速度的倒数或ITT。观察到的ITT，t是一个孔隙度相关参数（即它随孔隙度变化）。由于流体中的传输时间大于固体中的传输时间，因此观察到的通过岩石的传输时间随着孔隙度的增加而增加。

在绘制孔隙度相关参数与估计地层孔隙压力深度的关系图时，最好使用数学模型将正常压力趋势（在浅层沉积物中观察到）外推到地层压力异常的较深深度。通常，假设线性、指数或幂律关系，以便可以在笛卡尔、半对数或对数/对数纸上将正常压力趋势绘制为直线。在某些情况下，这些方法中的任何一种都无法观察到可接受的直线趋势，必须使用更复杂的模型。

根据Pennebaker技术，通过将异常压力与叠加速度的变化联系起来，可以预测异常压力。

Pennebaker观察到，ITT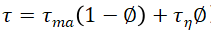（）不仅对地层深度具有幂律依赖性，而且还需要通过岩性进行补偿，而岩性又取决于压实历史。提出了基于100-μS/ft ITT深度的相关性来描述影响，并将其整合到地层压力估计中。事实上，一组相关性也被用来预测上覆压力和破裂压力。

根据Pennebaker关系式，可以用下列公式计算破裂压力梯度。

 

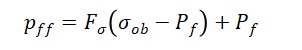
其中：

——破裂压力

——孔隙压力

——垂直上覆应力

——有效基体应力比

Pennebaker将基质应力比K和上覆梯度与深度进行了关联。与孔隙压力梯度（由标准Pennebaker图得出）一起，这些值用于估算破裂压力梯度。再次使用压实历史来校准相关性。

4. 理论实现（体积密度法为例）

体积密度法计算地层压力流程：

 

 

 

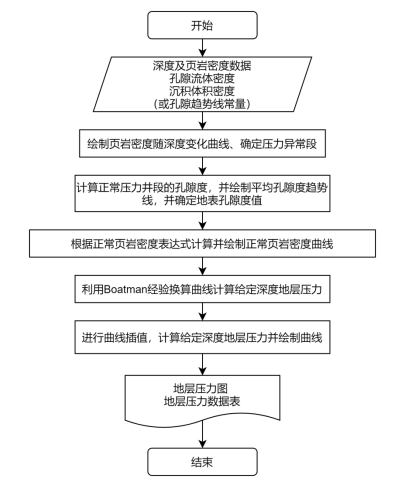
图2-1 体积密度法计算地层压力流程图

计算实例：利用下列地层密度数据（岩石骨架密度为2.649，平均流体密度为1.074），确定正常压力趋势线，并用Boatman换算曲线计算13,000英尺处地层孔隙压力。

表2-2 某口井地层密度表

沉积深度(ft)

体积密度(g/cm³)

地层平均孔隙度

6500

2.380

0.171

6600

2.371

0.177

6700

2.329

0.203

6800

2.340

0.196

6900

2.390

0.165

7000

2.390

0.165

7100

2.350

0.190

7500

2.409

0.152

7700

2.369

0.178

8000

2.390

0.165

8200

2.380

0.171

8300

2.340

0.196

8500

2.340

0.196

8900

2.409

0.152

9400

2.409

0.152

9500

2.409

0.152

9700

2.440

0.133

10000

2.440

0.133

10500

2.420

0.145

10600

2.460

0.120

10800

2.440

0.133

11100

2.440

0.133

11200

2.449

0.127

11400

2.449

0.127

11600

2.440

0.133

11900

2.460

0.120

11950

2.420

0.145

12100

2.440

0.133

12300

2.300

0.221

12400

2.210

0.278

12500

2.230

0.266

12600

2.220

0.272

13000

2.291

0.228

13100

2.260

0.247

13200

2.420

0.145

13400

2.249

0.254

13600

2.400

0.158

13800

2.279

0.235

14300

2.380

0.171

15000

2.380

0.171

15700

2.390

0.165

16100

2.420

0.145

 

第一步：绘制页岩密度随深度变化曲线、确定压力异常段。

 

 

 

根据页岩密度随深度变化散点图，确定正常地层压力为11000英尺深度以上。

 

第二步：计算正常压力地层的孔隙度，并绘制平均孔隙度趋势线，并确定地表孔隙度值。

 

 

 第三步：利用Boatman经验换算曲线计算给定深度地层压力。

 

 

 

 

 

 

 

 

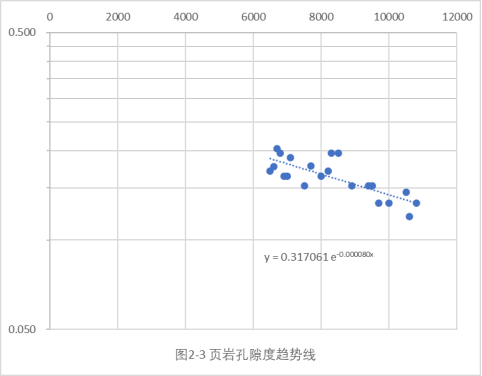
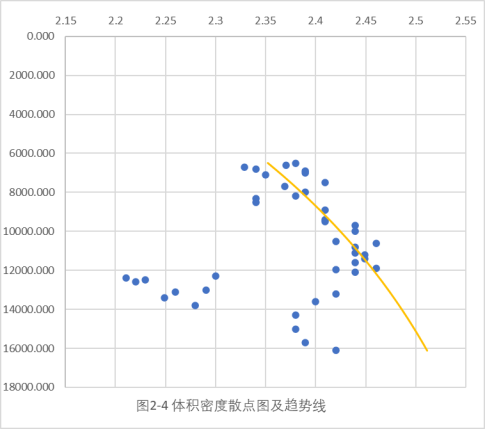
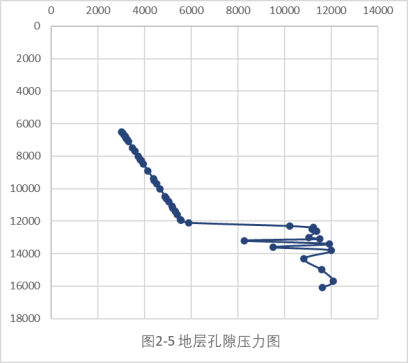
表2-3 地层压力计算结果

沉积深度(ft)

体积密度(g/cm³)

孔隙压力psig

6500

2.380

3028.984

6600

2.371

3075.584

6700

2.329

3122.183

6800

2.340

3168.783

6900

2.390

3215.383

7000

2.390

3261.983

7100

2.350

3308.582

7500

2.409

3494.981

7700

2.369

3588.181

8000

2.390

3727.98

8200

2.380

3821.18

8300

2.340

3867.779

8500

2.340

3960.979

8900

2.409

4147.378

9400

2.409

4380.377

9500

2.409

4426.976

9700

2.440

4520.176

10000

2.440

4659.975

10500

2.420

4892.974

10600

2.460

4939.574

10800

2.440

5032.773

11100

2.440

5172.572

11200

2.449

5219.172

11400

2.449

5312.372

11600

2.440

5405.571

11900

2.460

5545.37

11950

2.420

5568.67

12100

2.440

5906.978

12300

2.300

10213.15

12400

2.210

11249.78

12500

2.230

11184.02

12600

2.220

11373.17

13000

2.291

11055.83

13100

2.260

11502.96

13200

2.420

8267.262

13400

2.249

11925.37

13600

2.400

9510.268

13800

2.279

12008.34

14300

2.380

10834.92

15000

2.380

11584.44

15700

2.390

12088.55

16100

2.420

11611.51

 

 

 

 

 

 

5. 软件设计与实现

 

根据地层压力预测理论实现，结合可获得数据及应用需求，从实际能够获得的地质、录井、测井、地震数据出发，开发一个能够灵活应用，为综合判断钻井现场工程复杂、确定套管下深等提供理论依据。软件界面设计简单易用，利用鼠标进行标记压力异常层段，具有多语言切换，单位换算等功能，便于国内外钻井现场使用。

软件的主界面如下：

 

 

 

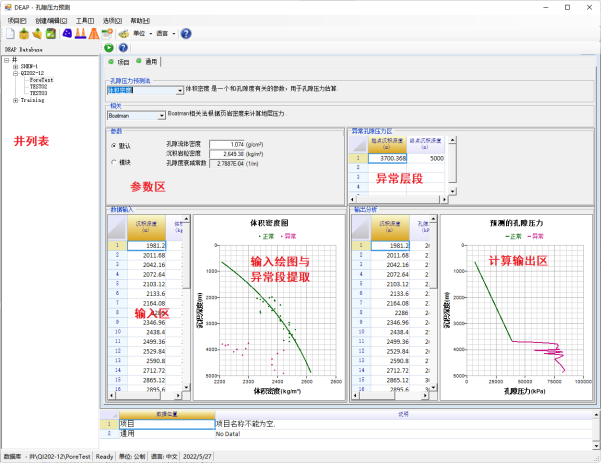
经过对各种计算方法的实际测试与应用，与对标软件高度一致。


 

posted @ 2022-05-27 13:57  智能油气田ing  阅读(582)  评论(1)  编辑  收藏  举报