『数据结构与算法』B树图文详解(含完整代码)
微信搜索:码农StayUp
主页地址:https://gozhuyinglong.github.io
源码分享:https://github.com/gozhuyinglong/blog-demos
1. 前言
迄今为止,已经介绍了《 二叉查找树 》和《 AVL树 》,我们始终假设可以把整个数据结构存储在内存中。可是,如果数据多到内存装不下,这就意味着必须把数据放在磁盘上,显然这些数据结构不再适用。
问题在于磁盘的I/O速度是远远不如内存访问速度的,然而从一棵树中查找到某个元素,必须从根节点一层层往下找,这每一次查找便是一次I/O操作。为了提高性能,就必须要减少查找的次数。
如能减少树的高度、增加每个节点中的元素数,便是种有效的解决方案。实现这种想法的一种方法是使用B树。
2. 术语
在介绍B树时会用到一些术语,这里先看一下:
- 根节点(root):没有父节点的节点叫做根节点
- 叶子节点(leaf):没有子节点的节点叫做叶子节点
- 内部节点(internal):除根节点和叶子节点之外的节点叫做内部节点。它们即有父节点,也有子节点。
- 键:B树中的存储元素是键,是用于指向数据记录的指针。键的值是用于存储真正的数据记录。一个节点中可以拥有多个键。
- 阶:B树的阶为最大子节点数量,其比键的数量大1。我们一般称一个B树为M阶的B树,那么该B树最多拥有M个子节点,节点中最多拥有M-1个键。
更多术语请参阅之前分享的《 树 》!
3. B树(B-Tree)
B树与二叉树(Binary Tree)不是一个概念,你可以将其翻译成
Balance Tree,或者是Bayer Tree。
B树是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。
B树与AVL树不同,可以拥有2个以上的子节点,并且每个节点可以有多个键值,这些属性减少了定位记录时所经历的中间过程,加快了存取速度。B树更适用于读写相对较大的数据块存储系统,如磁盘。这种数据结构常被应用在数据库和文件系统的实现上。
对于一个M阶B树具有以下特性:
- 每个节点最多有
M个子节点;每个内部节点最少有⌈M/2⌉个子节点(⌈x⌉为向上取整符号);如果根节点不是叶子节点,那么它至少有两个子节点。 - 具有
N个子节点的非叶子节点拥有N-1个键。 - 所有叶子节点必须处于同一层上。
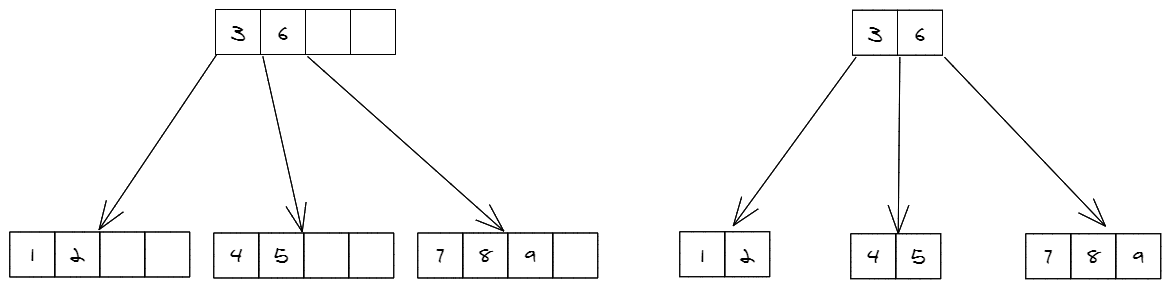
注:如下图是一棵5阶B树的两种画法,最准确的画法应该为图中左B树。但为了方便,通常会将节点中键为空的位置省去不画,如图中右B树。不能因为右图中最多的键为3,就判断这是一棵4阶B树,B树的阶是预先定义好的。
4. B树的操作
在对B树进行操作时,可能会违反B树的特性,如最小子节点数、每个节点最小键数。为了维护B树的这些特性,树可能会分裂或合并。
下面我们会以一棵5阶B树来讲述其搜索、插入、删除操作。先来看下5阶B树的特性:
- 内部节点至少有3个子节点(⌈5/2⌉ = 3),最多有5个子节点
- 每个节点至少有2个键(3-1=2),最多有4个键
4.1 搜索
B树的搜索和二叉搜索树类似,从根节点开始,从上往下递归的遍历树。在每一层节点上,使用二分查找法匹配目标键,或者通过键的范围来确定子树。
4.2 插入
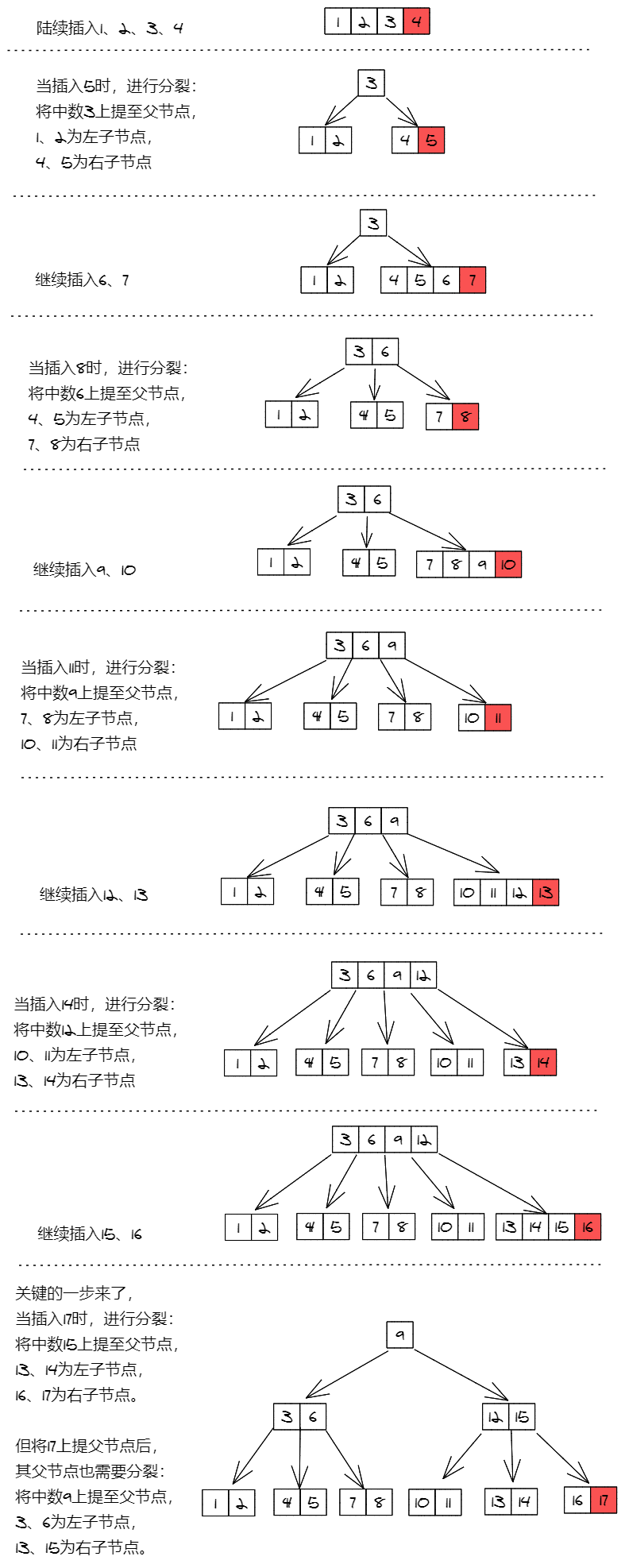
对于新元素的插入,都是发生在叶子节点上的。所有的插入操作都是从根节点开始,搜索这棵树,并找到该元素应该被插入的节点。将新元素插入到该节点需要如下步骤:
- 如果该节点上的元素数未满,则将新元素插入到该节点,并保持节点中元素的顺序。
- 如果该节点上的元素已满,则需要将该节点平均地分裂成两个节点:
- 从该节点中的元素和新元素先出一个中位数
- 小于中位数的元素放到左边节点,大于中位数的元素放到右边节点,中位数做为分隔值。
- 分隔值被插入到父节点中(增加了树的高度),这可能会导致父节点的分裂,分裂父节点时又可能会使它的父节点分裂,以此类推。如果分裂一直上升到根节点,那么就创建一个新的根节点,它有一个分隔值和两个子节点。(这就是根节点并不像内部节点一样有最少子节点数量限制的原因)
下图是一个5阶B树,我们通过顺序插入1到17,来观察节点的分裂过程。
4.3 删除
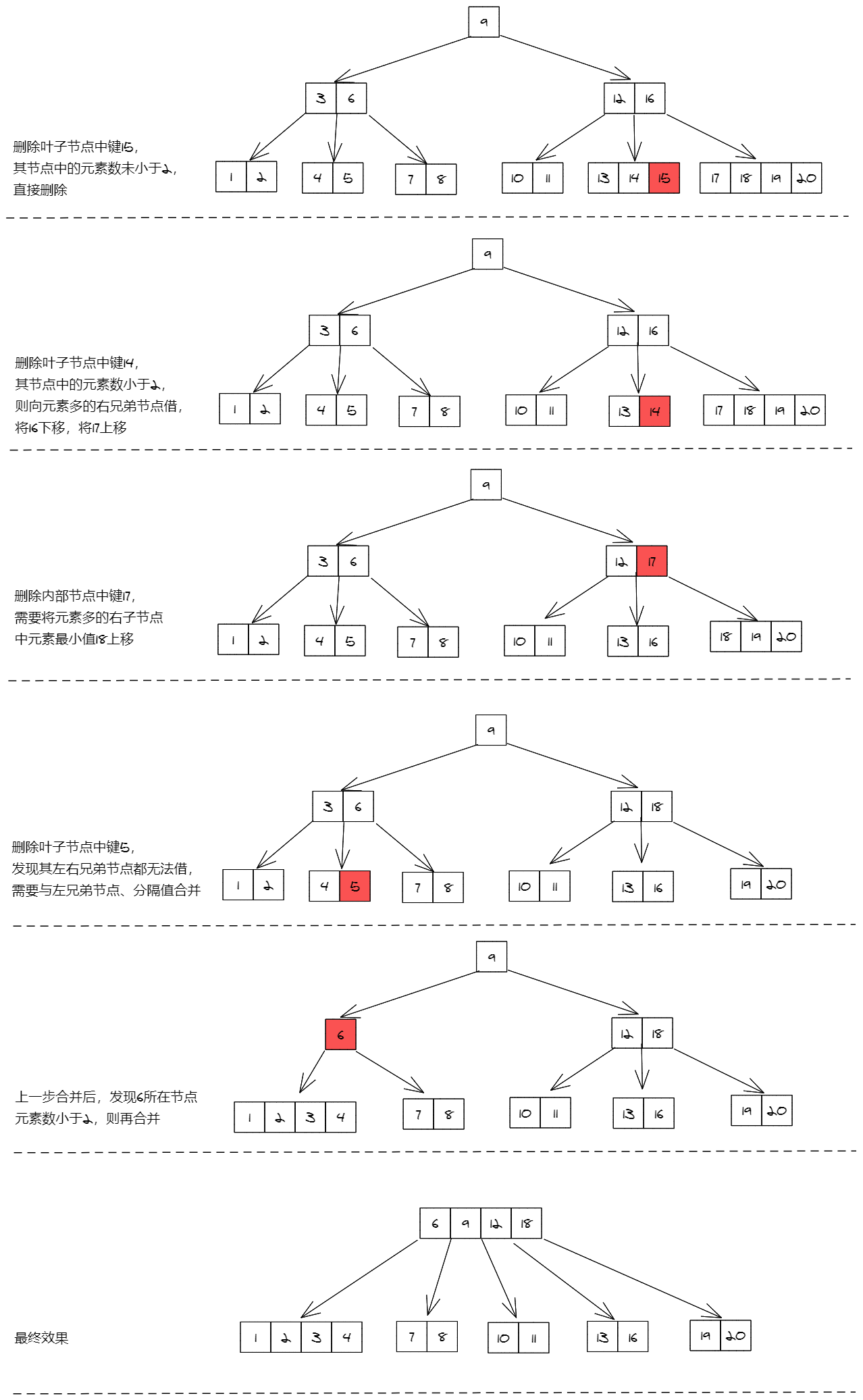
B树的删除就复杂了许多,可分为下面几种情况:
-
删除叶子节点中的元素
(1)搜索要删除的元素
(2)如果它在叶子节点上,直接将其删除
(3)如果删除后产生了下溢出(键数小于最小值),则向其兄弟节点借元素。即将其父节点元素下移至当前节点,将兄弟节点中元素上移至父节点(若是左节点,上移最大元素;若是右节点,上移最小元素)
(4)若兄弟节点也达到下限,则合并兄弟节点与分割键。 -
删除内部节点中的元素
(1)内部节点中元素为其左右子节点的分割值,需要从左子节点最大元素或右子节点最小元素中选出一个新的分割符。被选中的分割符从原子节点中移除,作为新的分隔值替换掉被删除的元素。
(2)上一步中,若左右子节点元素数均达到下限,则合并左右子节点。
(3)若删除元素后,其中节点元素数小于下限,则继续合并。
下图是一个5阶B树,我们通过删除15、14、17、5四个键,来观察删除过程(基本涵盖所有情况)。
5. 代码实现
本代码实现了B树的搜索、插入、删除操作,下面看详细介绍。
5.1 键值类
该类用于存放B树每个节点中的键值数据。
- key:节点中的键,用于指向数据记录。
- value:键向指向的数据记录。
由于键在节点中是顺序存储的,所以实现了Comparable接口
class Entry implements Comparable<Entry> {
final int key;
String value;
@Override
public int compareTo(Entry o) {
return Integer.compare(key, o.getKey());
}
}
5.2 节点类
节点类是B树中的每个节点,其主要包括:
- entrys:为该节点中所有的键,使用List类型存储
- childNodes:为该节点所有的子节点,使用List类型存储
- parentNode:为该节点的父节点。
由于childNodes需要排序,所以该类也实现了Comparable接口。
需要明白的一点是,当前节点中每个键的左右子节点都可以通过List集合的下标进行确定。比如:
entrys[0]的左右子节点分别为childNodes[0]、childNodes[1];
entrys[1]的左右子节点分别为childNodes[1]、childNodes[2],以此类推。
class Node implements Comparable<Node> {
private final List<Entry> entrys; // 当前节点的键值对
private final List<Node> childNodes; // 子节点,使用数组存储子节点
private Node parentNode; // 父节点
public Node() {
entrys = new ArrayList<>();
childNodes = new ArrayList<>();
}
public Node add(Entry entry) {
entrys.add(entry);
Collections.sort(entrys);
return this;
}
public Node addChild(Node node) {
childNodes.add(node);
Collections.sort(childNodes);
return this;
}
@Override
public int compareTo(Node o) {
return Integer.compare(entrys.get(0).getKey(), o.getEntrys().get(0).getKey());
}
}
5.3 B树类
B树类实现比较复杂,其主要属性包括:
- m:为B树的阶
- min:为B树中元素最小值,通过阶计算出
- root:树的根节点
class BTree {
private final int m; // B树的阶
private final int min;// 元素最小值
private Node root; // 树根
public BTree(int m) {
this.m = m;
this.min = (int) Math.ceil(m / 2.0) - 1;
}
public Node getRoot() {
return root;
}
}
5.4 搜索
B树的搜索实现较为简单,在BTree类中添加下面两个方法。
其二分查找法是通过Collections类中的binarySearch方法实现,感兴趣的话,可以研究下源码。后面会专门讲解二分查找法,这里就不多说了。
// 搜索
public Entry searchEntry(int key) {
return searchEntry(root, key);
}
// 搜索 - 递归
private Entry searchEntry(Node node, int key) {
if (node == null) {
return null;
}
// 使用二分查找法定位下标
int index = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
if (index >= 0) {
return node.getEntrys().get(index);
} else {
if (node.getChildNodes().size() == 0) {
return null;
}
return searchEntry(node.getChildNodes().get(-index - 1), key);
}
}
5.5 插入
B树的插入实现起来也不难,在BTree类中添加下面三个方法。
重要是split分离方法,如果添加一个元素后,其节点中元素值超过限定值,则进行分离操作,详细看代码。
// 添加元素
public void add(Entry entry) {
// root为空,直接创建
if (root == null) {
Node node = new Node();
node.add(entry);
root = node;
return;
}
add(root, entry);
}
// 添加元素 - 递归
private void add(Node node, Entry entry) {
// 当前节点为叶子节点
if (node.getChildNodes().size() == 0) {
// 如果当前节点元素未满,直接添加元素
if (node.getEntrys().size() < m - 1) {
node.add(entry);
return;
}
// 如果当前节点元素已满,则分裂当前节点
node.getEntrys().add(entry);
split(node);
return;
}
// 当前节点为内部节点,继续往下调用(新插入的节点,只能是叶子节点)
// 使用二分查找法找到要插入的分支
int index = Collections.binarySearch(node.getEntrys(), entry);
if (index < 0) {
add(node.getChildNodes().get(-index - 1), entry);
}
}
// 分离当前节点
private void split(Node node) {
int mid = node.getEntrys().size() / 2;
// 分隔值
Entry separateEntry = node.getEntrys().get(mid);
// 分离后的左节点
Node leftNode = new Node();
leftNode.getEntrys().addAll(node.getEntrys().subList(0, mid));
// 分离后的右节点
Node rightNode = new Node();
rightNode.getEntrys().addAll(node.getEntrys().subList(mid + 1, node.getEntrys().size()));
// 分离子节点
if (node.getChildNodes().size() > 0) {
List<Node> leftChildNode = node.getChildNodes().subList(0, mid + 1);
for (Node temp : leftChildNode) {
temp.setParentNode(leftNode);
}
leftNode.getChildNodes().addAll(leftChildNode);
List<Node> rightChildNode = node.getChildNodes().subList(mid + 1, node.getEntrys().size() + 1);
for (Node temp : rightChildNode) {
temp.setParentNode(rightNode);
}
rightNode.getChildNodes().addAll(rightChildNode);
}
// 当前节点为根节点
if (node.parentNode == null) {
Node newRoot = new Node();
newRoot.add(separateEntry);
root = newRoot;
leftNode.parentNode = root;
rightNode.parentNode = root;
root.addChild(leftNode).addChild(rightNode);
} else {
node.parentNode.add(separateEntry);
leftNode.parentNode = node.parentNode;
rightNode.parentNode = node.parentNode;
node.parentNode.addChild(leftNode).addChild(rightNode);
node.parentNode.getChildNodes().remove(node);
// 若其父节点溢出,继续分裂
if (node.parentNode.getEntrys().size() > m - 1) {
split(node.parentNode);
}
}
}
5.6 删除
B树的删除是最麻烦的,出现的情况太多了。
删除的节点主要为内部节点和叶子节点,每删除后都要判断当前节点中元素数是超出下限值。若超出下限值,需要根据情况进行判断。
若删除的是叶子节点,可能的操作时左旋转、右旋转、合并(当前节点、兄弟节点、中间值进行合并)。合并后又会出现其父节点超出下限值......
若删除的是内部节点,可能的操作时,合并左右兄弟节点、合并左右兄弟节点与中间值、向兄弟节点借元素。同样合并后也会出现其父节点超出下限......
public void remove(int key) {
// 先查询出当前元素所在节点
Node node = searchNode(key);
if (node == null) {
return;
}
// 删除节点
int keyIndex = Collections.binarySearch(node.getEntrys(), new Entry(key, null));
node.getEntrys().remove(keyIndex);
// 若当前节点的键数小于限定值,删除进行删除后处理
if (node.getEntrys().size() < min) {
afterDeletingHandler(node, keyIndex);
}
}
/**
* 删除后处理:当前节点元素数小于限定值,则根据不同场景选择进行合并、左旋转、右旋转
*
* @param node
*/
private void afterDeletingHandler(Node node, int deletedKeyIndex) {
// 该节点为内部节点
if (node.getChildNodes().size() > 0) {
// 获取删除元素的左右子节点
Node leftChideNode = node.getChildNodes().get(deletedKeyIndex);
Node rightChildNode = node.getChildNodes().get(deletedKeyIndex + 1);
int leftEntrysSize = leftChideNode == null ? 0 : leftChideNode.entrys.size();
int rightEntrysSize = rightChildNode == null ? 0 : rightChildNode.entrys.size();
int maxSize = Math.max(leftEntrysSize, rightEntrysSize);
// 先向左右子节点借
if (maxSize <= min) {
// 若左右子节点达到限定值,则合并左右子节点
merge(leftChideNode, rightChildNode);
return;
}
// 向左子节点借
Entry entry;
if (maxSize == leftEntrysSize) {
entry = leftChideNode.getEntrys().get(leftChideNode.getEntrys().size() - 1);
leftChideNode.getEntrys().remove(entry);
} else {
// 向右子节点借
entry = rightChildNode.getEntrys().get(0);
rightChildNode.getEntrys().remove(entry);
}
node.add(entry);
return;
}
// 该节点为叶子节点
Node parentNode = node.parentNode;
// 当前节点在父节点中的下标值
int nodeIndex = parentNode.getChildNodes().indexOf(node);
// 左兄弟节点
Node leftNode = nodeIndex > 0 ? parentNode.getChildNodes().get(nodeIndex - 1) : null;
// 右兄弟节点
Node rightNode = nodeIndex == parentNode.getChildNodes().size() - 1 ? null : parentNode.getChildNodes().get(nodeIndex + 1);
int leftEntrysSize = leftNode == null ? 0 : leftNode.entrys.size();
int rightEntrysSize = rightNode == null ? 0 : rightNode.entrys.size();
int maxSize = Math.max(leftEntrysSize, rightEntrysSize);
// 左右兄弟节点元素数均达到限定值,合并
if (maxSize <= min) {
if (leftNode != null) {
// 与左兄弟节点合并
merge(node, leftNode, nodeIndex - 1);
} else if (rightNode != null) {
// 与右兄弟节点合并
merge(node, rightNode, nodeIndex);
}
return;
}
if (maxSize == leftEntrysSize) {
// 向左节点借--> 右旋转
rightRotate(node, nodeIndex, leftNode);
} else {
// 向右节点借--> 左旋转
leftRotate(node, nodeIndex, rightNode);
}
}
/**
* 将当前节点与兄弟节点、中间值合并
*
* @param node 当前节点
* @param brotherNode 兄弟节点
* @param parentEntryIndex 中间值
*/
private void merge(Node node, Node brotherNode, int parentEntryIndex) {
// 创建新的节点
Node parentNode = node.getParentNode();
Node newNode = new Node();
newNode.getEntrys().addAll(node.getEntrys());
newNode.getEntrys().addAll(brotherNode.getEntrys());
newNode.add(parentNode.getEntrys().get(parentEntryIndex));
// 删除原节点及关系
parentNode.getEntrys().remove(parentEntryIndex);
parentNode.getChildNodes().remove(node);
parentNode.getChildNodes().remove(brotherNode);
if (node.getChildNodes().size() > 0) {
for (Node childNode : node.getChildNodes()) {
newNode.addChild(childNode);
childNode.setParentNode(newNode);
}
}
if (brotherNode.getChildNodes().size() > 0) {
for (Node childNode : brotherNode.getChildNodes()) {
newNode.addChild(childNode);
childNode.setParentNode(newNode);
}
}
// 若原节点为根节点,则当前节点为新的根节点
if (parentNode.getEntrys().size() == 0) {
root = newNode;
return;
} else {
parentNode.addChild(newNode);
newNode.setParentNode(parentNode);
}
// 合并后,若父节点的元素小于限定值,则再次合并(原则上是与最少元素数节点合并)
if (parentNode.getEntrys().size() < min) {
Node grandfatherNode = parentNode.getParentNode();
if (grandfatherNode == null) {
return;
}
int nodeIndex = Collections.binarySearch(grandfatherNode.getChildNodes(), parentNode);
// 左兄弟节点
Node leftNode = nodeIndex > 0 ? grandfatherNode.getChildNodes().get(nodeIndex - 1) : null;
// 右兄弟节点
Node rightNode = nodeIndex >= grandfatherNode.getChildNodes().size() - 1 ? null : grandfatherNode.getChildNodes().get(nodeIndex + 1);
int leftEntrysSize = leftNode == null ? 0 : leftNode.entrys.size();
int rightEntrysSize = rightNode == null ? 0 : rightNode.entrys.size();
int minSize = Math.min(leftEntrysSize, rightEntrysSize);
if (minSize > 0) {
if (leftEntrysSize == minSize) {
merge(parentNode, leftNode, nodeIndex - 1);
} else {
merge(parentNode, rightNode, nodeIndex);
}
} else if (leftEntrysSize > 0) {
merge(parentNode, leftNode, nodeIndex - 1);
} else if (rightEntrysSize > 0) {
merge(parentNode, rightNode, nodeIndex);
}
}
}
/**
* 合并两个兄弟节点
*
* @param node 当前节点
* @param brotherNode 兄弟节点
*/
private void merge(Node node, Node brotherNode) {
Node parentNode = node.getParentNode();
Node newNode = new Node();
newNode.getEntrys().addAll(node.getEntrys());
newNode.getEntrys().addAll(brotherNode.getEntrys());
Collections.sort(newNode.getEntrys());
newNode.setParentNode(parentNode);
parentNode.getChildNodes().remove(node);
parentNode.getChildNodes().remove(brotherNode);
parentNode.addChild(newNode);
}
/**
* 左旋转
* (1)将父节点的中间值元素删除,并添加到当前节点中
* (2)将右兄弟节点中最小元素删除,并添加到父节点中
*
* @param node 当前节点
* @param nodeIndex 中间值索引
* @param rightNode 右节点
*/
private void leftRotate(Node node, int nodeIndex, Node rightNode) {
Entry parentEntry = node.getParentNode().getEntrys().get(nodeIndex);
node.add(parentEntry);
node.getParentNode().getEntrys().remove(parentEntry);
Entry rightEntry = rightNode.getEntrys().get(0);
node.getParentNode().add(rightEntry);
rightNode.getEntrys().remove(rightEntry);
}
/**
* 右旋转
* (1)将父节点的中间值元素删除,并添加到当前节点中
* (2)将左兄弟节点中最大元素删除,并添加到父节点中
*
* @param node 当前节点
* @param nodeIndex 中间值索引
* @param leftNode 左节点
*/
private void rightRotate(Node node, int nodeIndex, Node leftNode) {
Entry parentEntry = node.getParentNode().getEntrys().get(nodeIndex - 1);
node.add(parentEntry);
node.getParentNode().getEntrys().remove(parentEntry);
Entry leftEntry = leftNode.getEntrys().get(leftNode.getEntrys().size() - 1);
node.getParentNode().add(leftEntry);
leftNode.getEntrys().remove(leftEntry);
}
6. 完整代码
完整代码篇幅过长,欢迎访问我的GitHub进行查看,若对您有帮助,也请给个Star!
推荐阅读
- 《 数组 》
- 《 稀疏数组 》
- 《 链表(单链表、双链表、环形链表) 》
- 《 栈 》
- 《 队列 》
- 《 树 》
- 《 二叉树 》
- 《 二叉查找树(BST) 》
- 《 AVL树(平衡二叉树) 》
- 《 B树 》
- 《 散列表(哈希表) 》
图文制作不易,您的关注将是我最大的动力!感谢~~🌹🌹🌹




