[模板]树状数组

树状数组在O(logN)时间内对数组执行单点增加,区间和查询.

观察这个树状数组:

其中,每个节点存储着其横向覆盖的范围内所有元素的和,如c[16]存储1~16号元素的和,c[12]存储9~12号元素的和.

节点x的覆盖范围表示为[x-lowbit(x)+1, x].

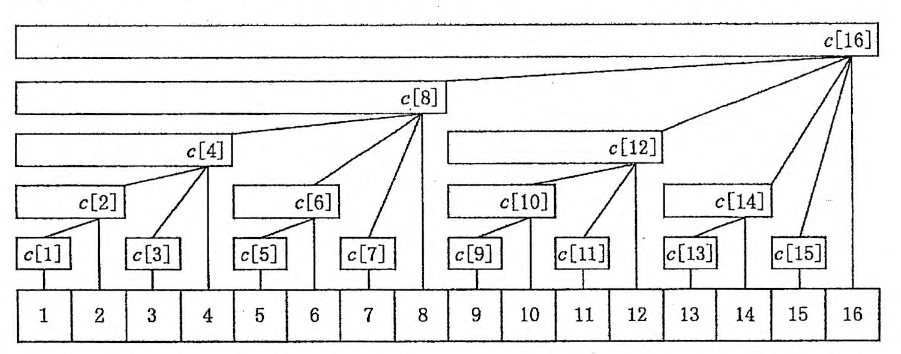
 从构造这颗树的角度来解释其结构,描述为每个节点c[x]的父节点都可以表示为c[x+lowbit(x)].

由此可推出树的深度为O(logN),这意味着从任意节点出发,都可以快速地遍历其到根节点的路径上的每一个点:

    while (x <= n) {
        operations on c[x]...
        x += lowbit(x);
    }

// 注: int lowbit(int x) { return x & -x; }

 

此外,从任意节点x出发,想要不重不漏地遍历1~x号元素只需要:

    while (x > 0) {
        operations on c[x]...
        x -= lowbit(x);
    }

 

以上就是树状数组支持的两种操作,复杂度都是O(logN).关于它为什么看起来像魔法,点这里.

由于树状数组的第二种操作,它很适合用来计算前缀和.

求取区间内所有数的和,使用前缀和表示,故维护树状数组c[i],操作1在位置x上加k,操作二计算前缀和c[1~y]与c[1~x-1]并输出两者差值.

int lowbit(int x) { return x & -x; }
void add(int x, int k) {        // 单点增加,在位置x增加k
    while (x <= n) {
        c[x] += k;
        x += lowbit(x);
    }
}
int sum(int x) {                // 区间和查询,求取前缀和c[1~x]
    int ret = 0;
    while (x > 0) {
        ret += c[x];
        x -= lowbit(x);
    }
    return ret;
}

故有:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

int n, m, s[500010];

int lowbit(int x) { return x & -x; }
void add(int x, int y) {
    while (x <= n) {
        s[x] += y;
        x += lowbit(x);
    }
}
int sum(int x) {
    int ans = 0;
    while (x > 0) {
        ans += s[x];
        x -= lowbit(x);
    }
    return ans;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        int x;
        scanf("%d", &x);
        add(i, x);
    }

    for (int i = 1; i <= m; ++i) {
        int opr, x, y;
        scanf("%d%d%d", &opr, &x, &y);
        if (opr == 1)
            add(x, y);
        else
            cout << sum(y) - sum(x - 1) << endl;
    }

    return 0;
}

 

既然有前缀和,对应地就可以运用差分解决如下问题:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

int n, m, s[500010], a[500010];

inline int lowbit(int x) {return x & -x;}
inline void add(int p, int x) {
    while(p <= n){
        s[p] += x;
        p += lowbit(p);
    }
}
inline int ask(int x){
    int ret = 0;
    while(x > 0){
        ret += s[x];
        x -= lowbit(x);
    }
    return ret;
}

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d", a + i);
    
    while(m--){
        int opr, x, y, k;
        scanf("%d", &opr);
        if(opr == 1){
            scanf("%d%d%d", &x, &y, &k);
            add(x, k);
            add(y + 1, -k);
        }else{
            scanf("%d", &x);
            printf("%d\n", a[x] + ask(x));
        }
    }

    return 0;
}

 

可以将树状数组的效果简单地总结为:对一序列进行频繁局部(单点)操作时,在任意时刻都可以快速求取当前序列的任意前缀和.

 

---

 

P1908 逆序对

如利用桶的思想,将数x置入桶c[x]中时,检查c[x+1~n]之和,即得新产生的逆序数.

树状数组满足了随时查询前缀和的操作.

需要处理一些细节,还有离散化.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

struct S {
    int num, val;
    bool operator<(S &other) const {
        return (val == other.val ? num < other.num : val < other.val);
    }
} s[500010];
int c[500010], rk[500010], n;

inline void add(int p, int d) {
    while (p <= n) {
        c[p] += d;
        p += p & -p;
    }
}
inline int ask(int p) {
    int ret = 0;
    while (p) {
        ret += c[p];
        p -= p & -p;
    }
    return ret;
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &s[i].val), s[i].num = i;

    sort(s + 1, s + 1 + n);
    long long ans = 0;
    for (int i = 1; i <= n; i++) rk[s[i].num] = i;
    for (int i = 1; i <= n; i++) {
        add(rk[i], 1);
        ans += i - ask(rk[i]);
    }

    printf("%lld\n", ans);

    return 0;
}

 

P3372 【模板】线段树 1

由于数学是美的,两个树状数组可以过了这道题.这里树状数组的作用仍然是快速求前缀和.

 

一篇更详细的博客:https://www.luogu.com.cn/blog/kingxbz/shu-zhuang-shuo-zu-zong-ru-men-dao-ru-fen