[CF1292D]Chaotic V.

昨晚#614div2的F题。我现在看感觉比E题还简单啊，为什么当时要去死刚E题呢。。。

题目大意：有一棵树，根节点编号为\(1\)，设一个节点的编号\(x(x>1)\)，则它的父节点编号为\(x/f(x)\)，边权为1，其中\(f(x)\)为\(x\)的最小质因子。现在给定\(n(n<=1000000)\)个编号为\(k_{1}!,k_{2}!,...,k_{n}!(0<=k_{i}<=5000)\)的点，你的任务是在这棵树 上确定一个点\(p\)使得\(\sum_{i}dis(p,k_{i}!)\)最小，输出这个最小值。

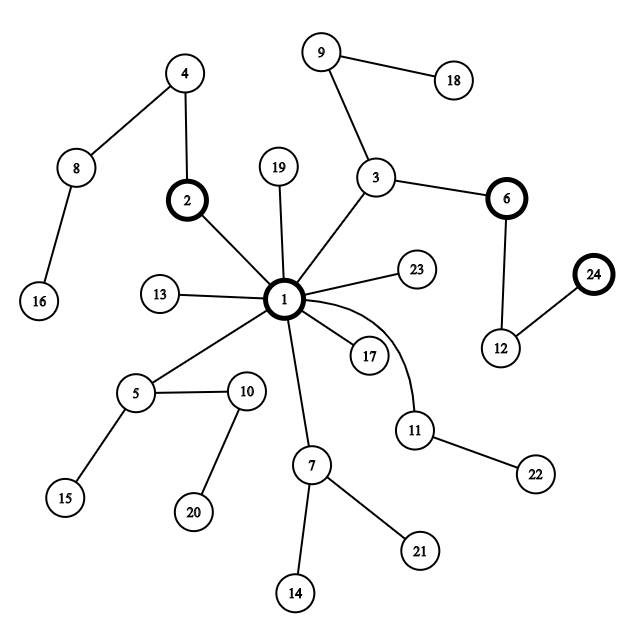
这棵树大概就长这个样子，其中边缘加粗的点分别是\(1!,2!,3!,4!\)

不妨把这\(n\)个点称为关键点，显然，\(k_{i}\)相同的关键点可以放在一起处理，那么\(n\)的规模退化到5000。
手玩一下发现，\(4!=3*2*2*2\)的位置是这样确定的：

\[1*3=3,3*2=6,6*2=12,12*2=24 \]

这启发我们是不是从根节点开始，从大到小依次乘\(x\)的质因子，最后就可以走到\(x\)？这是正确的。
好了，我们可以把\(0!,1!,...,5000!\)先分解一波质因子，就有办法确定这n个点在树上的位置关系了。
接下来考虑如何确定点\(p\)。
首先钦定\(p=1\)，然后尝试向把\(p\)向\(p\)的关键点最多的子树移动一步，设移动到\(p'\)

1. 如果\(p'\)能使答案更小，则\(p=p'\)，并重新统计\(p\)的各个子树关键点的数量；
2. 否则\(p\)就是使答案最小的点，退出循环。

移动一次维护关键点数量的复杂度为\(n\)，最多移动\(d(n!)\)次，\(d(n!)\)为\(n!\)的质因子数，它小于等于\(n!\)的约数个数，而\(n!\)的约数个数为\(nlogn\)，因此总的复杂度为\(O(n^2logn)\)。（这里\(n\)的规模为5000）
应该有更低的上界，但无所谓了。
代码就咕了。