c++(0) sophus库 R t T 四元数相互转换

 

void keyframe::set_cam_pose(const Mat44_t& cam_pose_cw) {
    std::lock_guard<std::mutex> lock(mtx_pose_);
    cam_pose_cw_ = cam_pose_cw;

    const Mat33_t rot_cw = cam_pose_cw_.block<3, 3>(0, 0);
    const Vec3_t trans_cw = cam_pose_cw_.block<3, 1>(0, 3);
    const Mat33_t rot_wc = rot_cw.transpose();
    cam_center_ = -rot_wc * trans_cw;

    cam_pose_wc_ = Mat44_t::Identity();
    cam_pose_wc_.block<3, 3>(0, 0) = rot_wc;
    cam_pose_wc_.block<3, 1>(0, 3) = cam_center_;
}

　　

 

 

 

0-1 R构造和四元数转换

 

#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>

int main()
{
    // 定义三个角度（弧度制）
    double yaw = 0.1;    // 绕Z轴的角度
    double pitch = 0.2;  // 绕Y轴的角度
    double roll = 0.3;   // 绕X轴的角度

    // 尺度因子 s
    double s = 2.0;

    // 构造旋转矩阵 R
    Eigen::Matrix3d R;
    R = Eigen::AngleAxisd(yaw, Eigen::Vector3d::UnitZ())
        * Eigen::AngleAxisd(pitch, Eigen::Vector3d::UnitY())
        * Eigen::AngleAxisd(roll, Eigen::Vector3d::UnitX());

    // 输出旋转矩阵 R
    std::cout << "Rotation matrix R:\n" << R << std::endl;

    // 将旋转矩阵 R 转换为四元数 q
    Eigen::Quaterniond q(R);

    // 输出四元数 q
    std::cout << "Quaternion q:\n" << q.coeffs().transpose() << std::endl;

    // 将四元数 q 乘以尺度因子 s
    q.coeffs() *= s;

    // 输出乘以尺度因子后的四元数 q
    std::cout << "Scaled Quaternion q:\n" << q.coeffs().transpose() << std::endl;

    // 将乘以尺度因子后的四元数 q 转换回旋转矩阵 R_new
    Eigen::Matrix3d R_new = q.toRotationMatrix();

    // 输出转换后的旋转矩阵 R_new
    std::cout << "Scaled Rotation matrix R_new:\n" << R_new << std::endl;

    // 求解四元数 q 的逆
    Eigen::Quaterniond q_inv = q.conjugate() / q.norm();

    // 输出四元数 q 的逆
    std::cout << "Quaternion q inverse:\n" << q_inv.coeffs().transpose() << std::endl;

    // 求解旋转矩阵 R 的逆（即转置矩阵）
    Eigen::Matrix3d R_inv = R.transpose();

    // 输出旋转矩阵 R 的逆
    std::cout << "Rotation matrix R inverse:\n" << R_inv << std::endl;

    return 0;
}

　　尺度 sss，四元数 qqq，和位移向量 ttt 构造位姿变换矩阵 TTT

 

#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>

int main()
{
    // 定义尺度因子 s
    double s = 2.0;

    // 定义四元数 q （示例为单位四元数）
    Eigen::Quaterniond q(1.0, 0.0, 0.0, 0.0);  // (w, x, y, z)

    // 定义位移向量 t
    Eigen::Vector3d t(1.0, 2.0, 3.0);

    // 构造旋转矩阵 R
    Eigen::Matrix3d R = q.toRotationMatrix();

    // 构造尺度矩阵 S
    Eigen::Matrix3d S = s * Eigen::Matrix3d::Identity();

    // 构造位姿变换矩阵 T
    Eigen::Matrix4d T = Eigen::Matrix4d::Identity();
    T.block<3, 3>(0, 0) = S * R;  // 前三行前三列为 sR
    T.block<3, 1>(0, 3) = t;      // 前三行第四列为 t

    // 输出位姿变换矩阵 T
    std::cout << "Transformation matrix T:\n" << T << std::endl;

    return 0;
}

　　

 

 

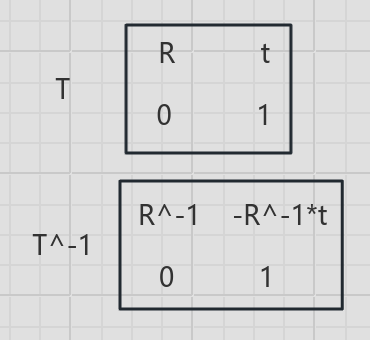
1-1 位姿矩阵 T和 Rt 变换 无尺度

    Matrix3d RelativeR;
    Vector3d Relativet;
    Relativet<<0,0,10;
    double currentScale=2;
    //RelativeR<<1,0,0,0,1,0,0,0,1;// 单位阵
    //RelativeR<<0,-1,0,1,0,0,0,0,1; // 旋转90度
    double yaw = 0;    // 绕Z轴的角度
    double pitch = 0;  // 绕Y轴的角度
    double roll = 0;   // 绕X轴的角度
    RelativeR = Eigen::AngleAxisd(yaw, Eigen::Vector3d::UnitZ())
          * Eigen::AngleAxisd(pitch, Eigen::Vector3d::UnitY())
          * Eigen::AngleAxisd(roll, Eigen::Vector3d::UnitX());
    cout<< "RelativeR "<<RelativeR <<endl;

　　

  // 假设位姿矩阵 T
  Eigen::Matrix4d T_vo_to_GNSS_ENU = Eigen::Matrix4d::Identity();
  T.block<3, 3>(0, 0) = Eigen::Matrix3d::Identity(); // 设置旋转部分为单位矩阵
  T.block<3, 1>(0, 3) << 0, 0, 0; // 设置平移部分为 (0, 0, 0)

  // 设置旋转部分
  //T.block<3, 3>(0, 0) = currentR; //Matrix3d currentR
  // 设置平移部分
  //T.block<3, 1>(0, 3) = currentT; // Vector3d currentT

  // Eigen::Matrix3d R_v_to_g = T.block<3, 3>(0, 0);
  // Eigen::Vector3d t_v_to_g = T.block<3, 1>(0, 3);

　　

1-2 位姿矩阵 T和 sRt 变换  s尺度作用在T的R上 （ svd分解 t=质心1-sR质心2）

#include <iostream>
#include <Eigen/Core>

int main()
{
    // 假设给定的尺度因子、旋转矩阵和平移向量
    double s = 2.0;
    Eigen::Matrix3d R = Eigen::Matrix3d::Identity(); // 假设为单位矩阵
    Eigen::Vector3d t(1.0, 2.0, 3.0); // 假设平移向量为 (1, 2, 3)

    // 初始化位姿矩阵 T
    Eigen::Matrix4d T = Eigen::Matrix4d::Identity();

    // 设置旋转矩阵 R（乘以尺度因子 s）
    T.block<3, 3>(0, 0) = s * R;

    // 设置平移向量 t
    T.block<3, 1>(0, 3) = t;

    // 输出位姿矩阵 T
    std::cout << "Pose Matrix T:\n" << T << std::endl;

    return 0;
}

　　

 

1-3 位姿矩阵 T和 sRt 变换  s尺度作用在整个T （不用 svd分解 s应该乘上R）

 

 

#include <iostream>
#include <Eigen/Core>

int main()
{
    // 假设给定的尺度因子、旋转矩阵和平移向量
    double s = 2.0;
    Eigen::Matrix3d R = Eigen::Matrix3d::Identity(); // 假设为单位矩阵
    Eigen::Vector3d t(1.0, 2.0, 3.0); // 假设平移向量为 (1, 2, 3)

    // 初始化位姿矩阵 T
    Eigen::Matrix4d T = Eigen::Matrix4d::Identity();

    // 设置旋转矩阵 R
    T.block<3, 3>(0, 0) = R;

    // 设置平移向量 t
    T.block<3, 1>(0, 3) = t;

    // 设置尺度因子 s
    T *= s;

    // 输出位姿矩阵 T
    std::cout << "Pose Matrix T:\n" << T << std::endl;

    return 0;
}

　　

 

 

 

 

1安装sophus

2 使用代码

2-1 R,t矩阵 q四元数转换so3和se3

 CMakeLists.txt

cmake_minimum_required(VERSION 3.0)
project(useSophus)

# 为使用 sophus，需要使用find_package命令找到它
find_package(Sophus REQUIRED)

# Eigen
include_directories("/usr/include/eigen3")
add_executable(useSophus useSophus.cpp)
target_link_libraries(useSophus Sophus::Sophus)

add_subdirectory(example)

　　useSophus.cpp

#include <iostream>
#include <cmath>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include "sophus/se3.hpp"

using namespace std;
using namespace Eigen;

/// 本程序演示sophus的基本用法

int main(int argc, char **argv) {

  // 沿Z轴转90度的旋转矩阵
  Matrix3d R = AngleAxisd(M_PI / 2, Vector3d(0, 0, 1)).toRotationMatrix();
  // 或者四元数
  Quaterniond q(R);
  Sophus::SO3d SO3_R(R);              // Sophus::SO3d可以直接从旋转矩阵构造
  Sophus::SO3d SO3_q(q);              // 也可以通过四元数构造
  // 二者是等价的
  cout << "SO(3) from matrix:\n" << SO3_R.matrix() << endl;
  cout << "SO(3) from quaternion:\n" << SO3_q.matrix() << endl;
  cout << "they are equal" << endl;

  // 使用对数映射获得它的李代数
  Vector3d so3 = SO3_R.log();
  cout << "so3 = " << so3.transpose() << endl;
  // hat 为向量到反对称矩阵
  cout << "so3 hat=\n" << Sophus::SO3d::hat(so3) << endl;
  // 相对的，vee为反对称到向量
  cout << "so3 hat vee= " << Sophus::SO3d::vee(Sophus::SO3d::hat(so3)).transpose() << endl;

  // 增量扰动模型的更新
  Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
  Sophus::SO3d SO3_updated = Sophus::SO3d::exp(update_so3) * SO3_R;
  cout << "SO3 updated = \n" << SO3_updated.matrix() << endl;

  cout << "*******************************" << endl;
  // 对SE(3)操作大同小异
  Vector3d t(1, 0, 0);           // 沿X轴平移1
  Sophus::SE3d SE3_Rt(R, t);           // 从R,t构造SE(3)
  Sophus::SE3d SE3_qt(q, t);            // 从q,t构造SE(3)
  cout << "SE3 from R,t= \n" << SE3_Rt.matrix() << endl;
  cout << "SE3 from q,t= \n" << SE3_qt.matrix() << endl;

 

  // 李代数se(3) 是一个六维向量，方便起见先typedef一下
  typedef Eigen::Matrix<double, 6, 1> Vector6d;
  Vector6d se3 = SE3_Rt.log();
  cout << "se3 = " << se3.transpose() << endl;
  // 观察输出，会发现在Sophus中，se(3)的平移在前，旋转在后.
  // 同样的，有hat和vee两个算符
  cout << "se3 hat = \n" << Sophus::SE3d::hat(se3) << endl;
  cout << "se3 hat vee = " << Sophus::SE3d::vee(Sophus::SE3d::hat(se3)).transpose() << endl;

  // 最后，演示一下更新
  Vector6d update_se3; //更新量
  update_se3.setZero();
  update_se3(0, 0) = 1e-4;
  Sophus::SE3d SE3_updated = Sophus::SE3d::exp(update_se3) * SE3_Rt;
  cout << "SE3 updated = " << endl << SE3_updated.matrix() << endl;

  return 0;
}

　　

// 提取平移和旋转部分

Eigen::Vector3d t_ij = T_ij.translation(); // j在 i坐标系下的位姿

Eigen::Matrix3d R_ij = T_ij.rotationMatrix(); // j在 i坐标系下的位姿

 

例子2  真值和测量值计算平均方误差

 

 

 CMakeLists.txt

option(USE_UBUNTU_20 "Set to ON if you are using Ubuntu 20.04" OFF)
find_package(Pangolin REQUIRED)
if(USE_UBUNTU_20)
    message("You are using Ubuntu 20.04, fmt::fmt will be linked")
    find_package(fmt REQUIRED)
    set(FMT_LIBRARIES fmt::fmt)
endif()
include_directories(${Pangolin_INCLUDE_DIRS})
add_executable(trajectoryError trajectoryError.cpp)
target_link_libraries(trajectoryError ${Pangolin_LIBRARIES} ${FMT_LIBRARIES})

　　trajectoryError.cpp

#include <iostream>
#include <fstream>
#include <unistd.h>
#include <pangolin/pangolin.h>
#include <sophus/se3.hpp>

using namespace Sophus;
using namespace std;

string groundtruth_file = "./example/groundtruth.txt";
string estimated_file = "./example/estimated.txt";

typedef vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> TrajectoryType;

void DrawTrajectory(const TrajectoryType &gt, const TrajectoryType &esti);

TrajectoryType ReadTrajectory(const string &path);

int main(int argc, char **argv) {
  TrajectoryType groundtruth = ReadTrajectory(groundtruth_file);
  TrajectoryType estimated = ReadTrajectory(estimated_file);
  assert(!groundtruth.empty() && !estimated.empty());
  assert(groundtruth.size() == estimated.size());

  // compute rmse
  double rmse = 0;
  for (size_t i = 0; i < estimated.size(); i++) {
    Sophus::SE3d p1 = estimated[i], p2 = groundtruth[i];
    double error = (p2.inverse() * p1).log().norm();
    rmse += error * error;
  }
  rmse = rmse / double(estimated.size());
  rmse = sqrt(rmse);
  cout << "RMSE = " << rmse << endl;

  DrawTrajectory(groundtruth, estimated);
  return 0;
}

TrajectoryType ReadTrajectory(const string &path) {
  ifstream fin(path);
  TrajectoryType trajectory;
  if (!fin) {
    cerr << "trajectory " << path << " not found." << endl;
    return trajectory;
  }

  while (!fin.eof()) {
    double time, tx, ty, tz, qx, qy, qz, qw;
    fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
    Sophus::SE3d p1(Eigen::Quaterniond(qw, qx, qy, qz), Eigen::Vector3d(tx, ty, tz));
    trajectory.push_back(p1);
  }
  return trajectory;
}

void DrawTrajectory(const TrajectoryType &gt, const TrajectoryType &esti) {
  // create pangolin window and plot the trajectory
  pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
  glEnable(GL_DEPTH_TEST);
  glEnable(GL_BLEND);
  glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

  pangolin::OpenGlRenderState s_cam(
      pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
      pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
  );

  pangolin::View &d_cam = pangolin::CreateDisplay()
      .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
      .SetHandler(new pangolin::Handler3D(s_cam));


  while (pangolin::ShouldQuit() == false) {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    d_cam.Activate(s_cam);
    glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

    glLineWidth(2);
    for (size_t i = 0; i < gt.size() - 1; i++) {
      glColor3f(0.0f, 0.0f, 1.0f);  // blue for ground truth
      glBegin(GL_LINES);
      auto p1 = gt[i], p2 = gt[i + 1];
      glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
      glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
      glEnd();
    }

    for (size_t i = 0; i < esti.size() - 1; i++) {
      glColor3f(1.0f, 0.0f, 0.0f);  // red for estimated
      glBegin(GL_LINES);
      auto p1 = esti[i], p2 = esti[i + 1];
      glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
      glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
      glEnd();
    }
    pangolin::FinishFrame();
    usleep(5000);   // sleep 5 ms
  }

}