优化原理 （1）高斯牛顿 线性

 

 

 

 

/*
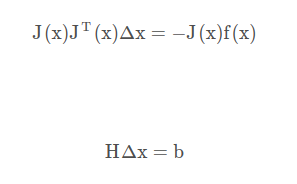
* Gauss-Newton iteration method
* author:Davidwang
* date  :2020.08.24
*/
#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

void GN(const int, vector<double> &, vector<double> &, double &, double &, double &, double const);

int main(int argc, char **argv)
{
    double ar = 18.0, br = 2.0, cr = 1.0; // 真实参数值
    double ae = 2.0, be = 4.0, ce = 3.0;  // 估计参数值
    int N = 50;                           // 数据点
    double w_sigma = 1.0;                 // 噪声Sigma值
    double inv_sigma = 1.0 / w_sigma;     // 信息值
    cv::RNG rng;                          // OpenCV随机数产生器

    vector<double> x_data, y_data; // 生成真值数据
    for (int i = 0; i < N; i++)
    {
        double x = i / 100.0;
        x_data.push_back(x);
        y_data.push_back(ar * x + exp(br * x + cr) + rng.gaussian(w_sigma * w_sigma));
    }

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    GN(N, x_data, y_data, ae, be, ce, inv_sigma);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);

    cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
    cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
    return 0;
}

///高斯牛顿法，N数据个数，x:X值，y:Y值，ae:a估计值，be:b估计值，ce:c估计值，inv_sigma:信息值（1/σ）
void GN(const int N, vector<double> &x, vector<double> &y, double &ae, double &be, double &ce, double const inv_sigma)
{
    int iterations = 50;           // 迭代次数
    double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost
    double xi, yi, error, e;

    for (int iter = 0; iter < iterations; iter++)
    {
        Matrix3d H = Matrix3d::Zero();
        Vector3d b = Vector3d::Zero();
        cost = 0;

        for (int i = 0; i < N; i++)
        {
            xi = x[i], yi = y[i];            // 第i个数据点
            e = ae * xi + exp(be * xi + ce); // 计算估计值
            error = yi - e;                  // 误差
            Vector3d J;                      // 雅可比矩阵
            J[0] = -xi;                      // de/da
            J[1] = -xi * exp(be * xi + ce);  // de/db
            J[2] = -exp(be * xi + ce);       // de/dd

            H += inv_sigma * inv_sigma * J * J.transpose(); //H = J^T * W^{-1} * J,inv_sigma 为信息值，本示例可以去掉
            b += -inv_sigma * inv_sigma * error * J;        //b= -W^{-1} * f(x)*J ,inv_sigma 为信息值，本示例可以去掉

            cost += error * error;

            cout << "The " << iter + 1 << " iteration, The " << i << " factor " << endl;
            cout << "THe Value, x: " << xi << ",y:" << yi << ",e:" << e << ",error:" << error << endl
                 << endl;
        }
        Vector3d dx = H.ldlt().solve(b); // 求解线性方程 HΔx=b
        if (isnan(dx[0]))
        {
            cout << "result is nan!" << endl;
            break;
        }

        if (iter > 0 && cost >= lastCost)
        {
            cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
            break;
        }

        ae += dx[0];
        be += dx[1];
        ce += dx[2];

        lastCost = cost;

        cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() << "\t\testimated params: " << ae << "," << be << "," << ce << endl;
    }
}

　　

 CMakeLists如下：

cmake_minimum_required(VERSION 2.8)
project(gaussNewton)

set(CMAKE_BUILD_TYPE Release)
set(CMAKE_CXX_FLAGS "-std=c++14 -O3")

list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)

# OpenCV
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})

# Eigen
include_directories("/usr/include/eigen3")

add_executable(GN gaussNewton_GN.cpp)
target_link_libraries(GN ${OpenCV_LIBS})