https://github.com/mengxingshifen1218/learning-pointcloud/blob/master/%E6%B7%B1%E8%93%9D/CH1/PointCloudHomework1/pca_normal.py

KD-Tree原理详解
https://zhuanlan.zhihu.com/p/112246942
构建算法:
Input: 无序化的点云,维度k
Output:点云对应的kd-tree
Algorithm:
1、初始化分割轴:对每个维度的数据进行方差的计算,取最大方差的维度作为分割轴,标记为r;
2、确定节点:对当前数据按分割轴维度进行检索,找到中位数数据,并将其放入到当前节点上;
3、划分双支:
划分左支:在当前分割轴维度,所有小于中位数的值划分到左支中;
划分右支:在当前分割轴维度,所有大于等于中位数的值划分到右支中。
4、更新分割轴:r = (r + 1) % k;
5、确定子节点:
确定左节点:在左支的数据中进行步骤2;
确定右节点:在右支的数据中进行步骤2;拿个例子说明为:
二维样例:{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}
构建步骤:
1、初始化分割轴:
发现x轴的方差较大,所以,最开始的分割轴为x轴。
2、确定当前节点:
对{2,5,9,4,8,7}找中位数,发现{5,7}都可以,这里我们选择7,也就是(7,2);
3、划分双支数据:
在x轴维度上,比较和7的大小,进行划分:
左支:{(2,3),(5,4),(4,7)}
右支:{(9,6),(8,1)}
4、更新分割轴:
一共就两个维度,所以,下一个维度是y轴。
5、确定子节点:
左节点:在左支中找到y轴的中位数(5,4),左支数据更新为{(2,3)},右支数据更新为{(4,7)}
右节点:在右支中找到y轴的中位数(9,6),左支数据更新为{(8,1)},右支数据为null。
6、更新分割轴:
下一个维度为x轴。
7、确定(5,4)的子节点:
左节点:由于只有一个数据,所以,左节点为(2,3)
右节点:由于只有一个数据,所以,右节点为(4,7)
8、确定(9,6)的子节点:
左节点:由于只有一个数据,所以,左节点为(8,1)
右节点:右节点为空。
最终,就可以构建整个的kd-tree了。
示意图如下所示 [1] :
二维空间表示:
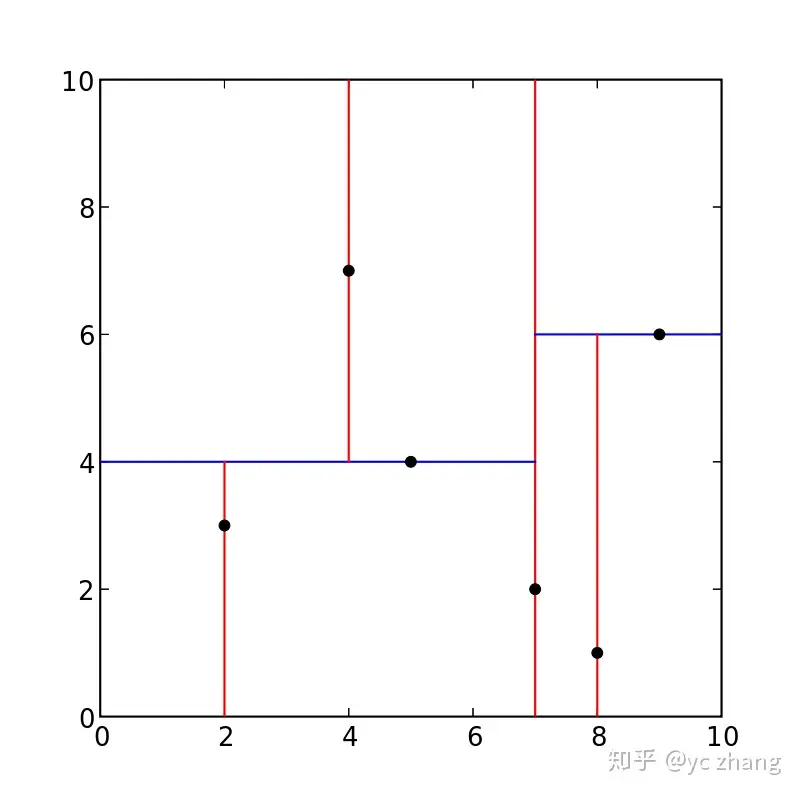
二维坐标系下的分割示意图
kd-tree表示:
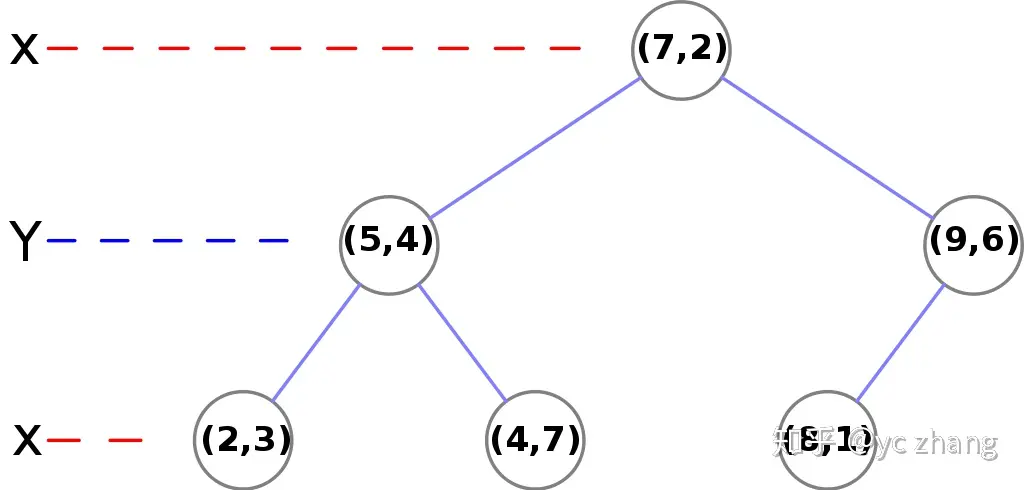
2.3、最近邻检索
在构建了完整的kd-tree之后,我们想要使用他来进行高维空间的检索。所以,这里讲解一下比较常用的最近邻检索,其中范围检索也是同样的道理。
最近邻搜索,其实和之前我们曾经学习过的KNN很像。不过,在激光点云章,如果使用常规的KNN算法的话,时间复杂度会空前高涨。因此,为了减少时间消耗,在工程上,一般使用kd-tree进行最近邻检索。
由于kd-tree已经按照维度进行划分了,所以,我们在进行比较的时候,也可以通过维度进行比较,来快速定位到与其最接近的点。由于可能会进行多个最近邻点的检索,所以,算法也可能会发生变化。因此,我将从最简单的一个最近邻开始说起。
整体求解
实现PCA分析和法向量计算,并加载数据集中的文件进行验证
import open3d as o3d
# import os
import numpy as np
from scipy.spatial import KDTree
# from pyntcloud import PyntCloud
# 功能:计算PCA的函数
# 输入:
# data:点云,NX3的矩阵
# correlation:区分np的cov和corrcoef,不输入时默认为False
# sort: 特征值排序,排序是为了其他功能方便使用,不输入时默认为True
# 输出:
# eigenvalues:特征值
# eigenvectors:特征向量
def PCA(data, correlation=False, sort=True):
# normalize 归一化
mean_data = np.mean(data, axis=0)
normal_data = data - mean_data
# 计算对称的协方差矩阵
H = np.dot(normal_data.T, normal_data)
# SVD奇异值分解,得到H矩阵的特征值和特征向量
eigenvectors, eigenvalues, _ = np.linalg.svd(H)
if sort:
sort = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[sort]
eigenvectors = eigenvectors[:, sort]
return eigenvalues, eigenvectors
def main():
# 从txt文件获取点,只对点进行处理
filename = "D:\pointcloud_processing\modelnet40_normal_resampled\\airplane\\airplane_0001.txt"
points = np.loadtxt(filename, delimiter=',')[:, 0:3] # 导入txt数据到np.array,这里只需导入前3列
print('total points number is:', points.shape[0])
# 用PCA分析点云主方向
w, v = PCA(points) # PCA方法得到对应的特征值和特征向量
point_cloud_vector = v[:, 0] #点云主方向对应的向量为最大特征值对应的特征向量
print('the main orientation of this pointcloud is: ', point_cloud_vector)
# 三个特征向量组成了三个坐标轴
axis = o3d.geometry.TriangleMesh.create_coordinate_frame().rotate(v, center=(0, 0, 0))
# 循环计算每个点的法向量
leafsize = 32 # 切换为暴力搜索的最小数量
KDTree_radius = 0.1 # 设置邻域半径
tree = KDTree(points, leafsize=leafsize) # 构建KDTree
radius_neighbor_idx = tree.query_ball_point(points, KDTree_radius) # 得到每个点的邻近索引
normals = [] # 定义一个空list
# -------------寻找法线---------------
# 首先寻找邻域内的点
for i in range(len(radius_neighbor_idx)):
neighbor_idx = radius_neighbor_idx[i] # 得到第i个点的邻近点索引,邻近点包括自己
neighbor_data = points[neighbor_idx] # 得到邻近点,在求邻近法线时没必要归一化,在PCA函数中归一化就行了
eigenvalues, eigenvectors = PCA(neighbor_data) # 对邻近点做PCA,得到特征值和特征向量
normals.append(eigenvectors[:, 2]) # 最小特征值对应的方向就是法线方向
# ------------法线查找结束---------------
normals = np.array(normals, dtype=np.float64) # 把法线放在了normals中
# o3d.geometry.PointCloud,返回了PointCloud类型
pc_view = o3d.geometry.PointCloud(points=o3d.utility.Vector3dVector(points))
# 向PointCloud对象中添加法线
pc_view.normals = o3d.utility.Vector3dVector(normals)
# 可视化
o3d.visualization.draw_geometries([pc_view, axis], point_show_normal=True)
if __name__ == '__main__':
main()



