库安装
https://www.cnblogs.com/gooutlook/p/14831906.html
工程测试

CMakeLists.txt
cmake_minimum_required(VERSION 3.1)
project(useEigen)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")
# 添加Eigen头文件
find_package(Eigen3 REQUIRED)
#include_directories("/usr/include/eigen3")
include_directories("/usr/local/include/eigen3")
add_executable(v0_eigenMatrix v0_eigenMatrix.cpp)
add_executable(v1_eigenMatrix v1_eigenMatrix.cpp)
v0_eigenMatrix.cpp

#include <iostream>
using namespace std;
#include <ctime>
// Eigen 核心部分
#include <Eigen/Core>
// 稠密矩阵的代数运算(逆,特征值等)
#include <Eigen/Dense>
using namespace Eigen;
/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/
int main(int argc, char **argv) {
// 1-1-1 创建通用矩阵 声明一个2*3的float矩阵
// Eigen 中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为:数据类型,行,列
Matrix<float, 2, 3> matrix_23;
// 1-2-1 创建特定矩阵 内置好了,本质上还是通用矩阵Matrix<>
Vector3d v_3d;//3*1 float eigen::Matrix<double, 3, 1>,即三维向量
// 等价通用矩阵
Matrix<float, 3, 1> vd_3d;//3*1 float
// 1-2-2 创建特定矩阵 内置好了,本质上还是通用矩阵Matrix<>
// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>
Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零
// 2下面是对Eigen阵的操作
// 2-1 输入数据(初始化)
matrix_23 << 1, 2, 3, 4, 5, 6;
// 输出
cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;
// 2-2 用()访问矩阵中的元素
cout << "print matrix 2x3: " << endl;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 3; j++) cout << matrix_23(i, j) << "\t";
cout << endl;
}
// 2-3 矩阵和向量相乘(实际上仍是矩阵和矩阵)
v_3d << 3, 2, 1; //v_3d Eigen::Matrix<double, 3, 3>
vd_3d << 4, 5, 6;
// 格式应该一样
// matrix_23 Matrix<float, 2, 3>
// v_3d Matrix<double, 3, 1>
// vd_3d Matrix<float, 3, 1>
// matrix_23*v_3d 应该显式转换
Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;
cout << "[1,2,3; \n 4,5,6]*[3,2,1]=" << result.transpose() << endl;
// matrix_23*vd_3d 格式一样不需要转换
Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
cout << "[1,2,3; \n 4,5,6]*[4,5,6]: " << result2.transpose() << endl;
// 3 一些矩阵运算
// 3-1 四则运算就不演示了,直接用+-*/即可。
// 3-2
matrix_33 = Matrix3d::Random(); // 随机数矩阵
cout << "random matrix: \n" << matrix_33 << endl;
cout << "transpose: \n" << matrix_33.transpose() << endl; // 转置
cout << "inverse: \n" << matrix_33.inverse() << endl; // 逆
cout << "sum: " << matrix_33.sum() << endl; // 各元素和
cout << "trace: " << matrix_33.trace() << endl; // 迹
cout << "times 10: \n" << 10 * matrix_33 << endl; // 数乘
cout << "det: " << matrix_33.determinant() << endl; // 行列式
// 3-3 特征值
// 实对称矩阵可以保证对角化成功
SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;
// 3-4 解方程 除法======================================
// 我们求解 matrix_NN * x = v_Nd 这个方程
// N的大小在前边的宏里定义,它由随机数生成
// 直接求逆自然是最直接的,但是求逆运算量大
const int MATRIX_SIZE= 3;//矩阵大小默认了就不能改变
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN
= MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
matrix_NN = matrix_NN * matrix_NN.transpose(); // 保证半正定
Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);
clock_t time_stt = clock(); // 计时
// 3-4-1直接求逆
Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;
cout << "time of normal inverse is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
// 3-4-2 通常用矩阵分解来求,例如QR分解,速度会快很多
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout << "time of Qr decomposition is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
// 3-4-3对于正定矩阵,还可以用cholesky分解来解方程
time_stt = clock();
x = matrix_NN.ldlt().solve(v_Nd);
cout << "time of ldlt decomposition is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
return 0;
}
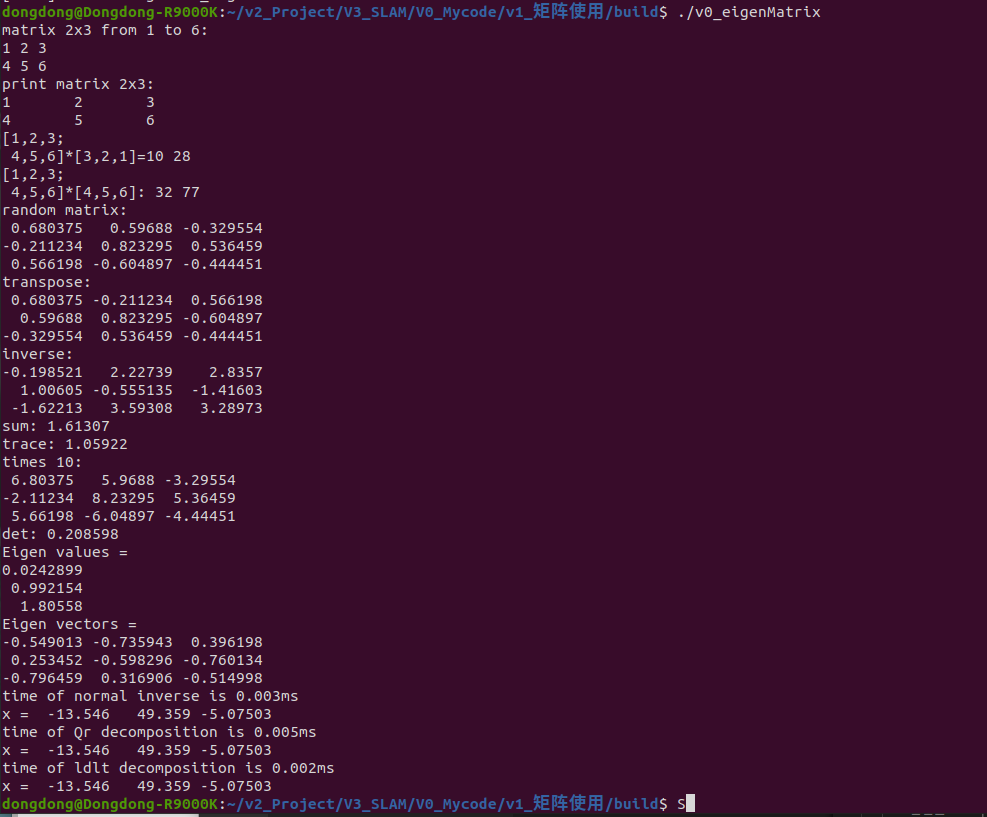
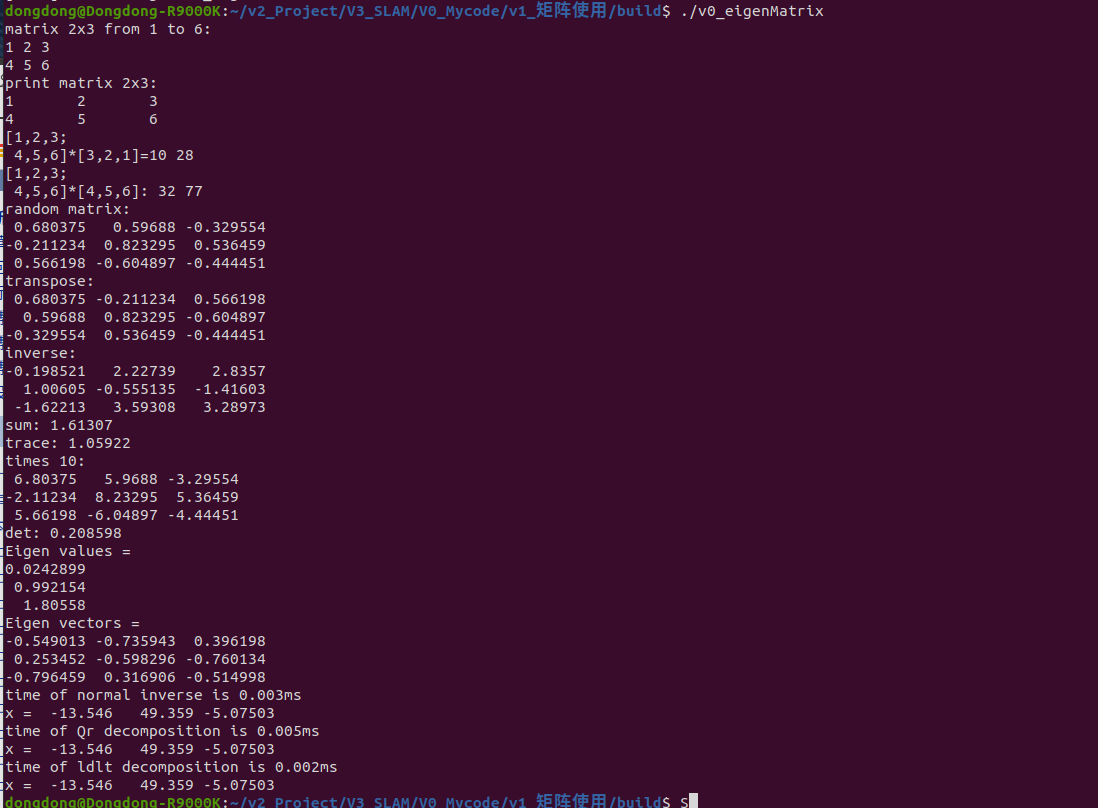
编译
0 安装库 sudo apt-get install libeigen3-dev 1 编译 cd build camke .. make 2运行 ./v0_eigenMatrix ./v1_eigenMatrix