https://cloud.tencent.com/developer/article/1483521
最近公众号组织了ORB-SLAM2理论与代码的学习会,正常进行中,有兴趣的可以积极参与第三期:一起来学SLAM
其中ORB-SLAM点云地图中相机的位姿初始化,无论算法工作在平面场景,还是非平面场景下,都能够完成初始化的工作。其中主要是使用了适用于平面场景的单应性矩阵H和适用于非平面场景的基础矩阵F,程序中通过一个评分规则来选择适合的模型,恢复相机的旋转矩阵R和平移矩阵t
那么下面主要讲解关于对极几何中的基础矩阵,本质矩阵,和单应矩阵之间的区别与联系。
对极几何(Epipolar Geometry)描述的是两幅视图之间的内在射影关系,与外部场景无关,只依赖于摄像机内参数和这两幅视图之间的相对位姿。

两视图的对极几何可以理解为图像平面与以基线为轴的平面束相交的几何关系,其中主要有几种概念:
(1)基线(base line):两个相机中心的连线CC'称为基线。
(2)对极点(epipolar):ee'是对极点,是基线与两个成像平面的交点,也就是两个相机在另一个成像平面上的像点。
(3)对极平面(epipolar plane):过基线的平面都称之为对极平面,其中两个相机的中心C和C',三维点X,以及三维点在两个相机成像点xx'这五点必定在同一对极平面上,当三维点X变化时,对极平面绕着基线旋转,形成对极平面束。
(4)对极线(epipolar line):是对极平面和成像平面的交线,所有的对极线都相交于极点。
那么由对极几何的基本性质引出了对极约束的概念,对极约束是指在平面2上的p点在平面1上的对应点一定在基线I'上,这句话说明了对极约束是一个点到直线的射影映射关系。如图所示:

根据对极约束可以引出本质矩阵和基础矩阵。在已知相机标定的情况下,假设有一个三维坐标点P(X,Y,Z)在两个视图上的点分别为p1,p2,由于第一个相机的中心作为世界坐标系的原点,也就是说第一个相机没有旋转R和平移t,通过小孔相机模型有:
p1=KP, p2=K(RP+t)
其中,K是相机的内参,R,t是第二个相机相对于第一个相机的旋转和平移。
从p1=KP可以得到

带入到第二个式子得到

两边同时乘以K_1得到

为了方便计算,使用简化符号 x1,和x2表示为

带入到 中,
中,
两边同时左乘向量t的反对称矩阵t×,由于t×t=0,消除t,
==========反对称矩阵=============
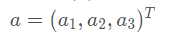
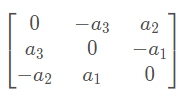
==========反对称矩阵=============

两边再同时左乘xT2

由于t×x2是向量t和向量x2的叉积,同时垂直于向量t和向量x2,所以左边的式子为0得到:

将x1,x2替掉

上式是对极约束的一种表示,该式子中仅包含像点,相机的旋转和平移,中间的矩阵就是基础矩阵F:

当K已知时提取中间的矩阵得到本质矩阵E,E矩阵同样表示的是对极约束的关系,只不过它不再涉及相机内参,只由两视图之间的姿态关系决定:

F矩阵的性质有三:
1, 3*3且自由度为7的矩阵
2,kF 为基础矩阵,相差一个尺度自由度
3,F矩阵的秩为2
基础矩阵的求解方法:
1,直接线性变换法(8点法+最小二乘法)
2,RANSAC-估计基础矩阵



