旋转图像

48. 旋转图像

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

思路

元素 (i, j) 对应的四个位置分别是：

• (i, j)
• (N-1-j, i)
• (N-1-i, N-1-j)
• (j, N-1-i)

如果 n 是偶数的话，这相当于把矩阵均分成四块，每块的元素个数是 \(( n / 2 ) \times ( n / 2 )\)。如果 n 是奇数，矩阵的中心元素是不随旋转移动的，而剩下的元素均分成四块，每块的元素个数是\((n/2) \times (n/2)\)。对一块中的所有元素做一次四元素旋转即可。

坐标怎么来的？数学方法：

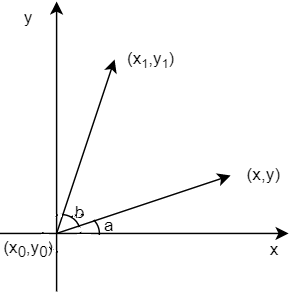
将\((x,y)\) 绕 \((x_0,y_0)\) 逆时针旋转 \(b\) 度，表示如下：

\[\begin{cases}x = l \times cos(a)\\y = l \times sim(a)\\x_1 = l \times cos(a+b)\\y_1 = l \times sin(a+b)\end{cases} \]

得：

\[x_1 = x \times cos(b) - y\times sin(b)\\y_1 = x \times sin(b)-y\times cos(b) \]

所以将 (i,j) 顺时针转90度的坐标依次为：

(i, j) $ \rightarrow$ (j, N-1-i) $ \rightarrow$ (N-1-i, N-1-j) $ \rightarrow$ (N-1-j, i)

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        if not matrix:
            return []
        n = len(matrix)
        for i in range(n//2+n%2):
            for j in range(n//2):
                temp = matrix[i][j]
                matrix[i][j] = matrix[n-j-1][i]
                matrix[n-j-1][i] = matrix[n-i-1][n-j-1]
                matrix[n-i-1][n-j-1] = matrix[j][n-i-1]
                matrix[j][n-i-1] = temp

        return matrix