排序算法学习
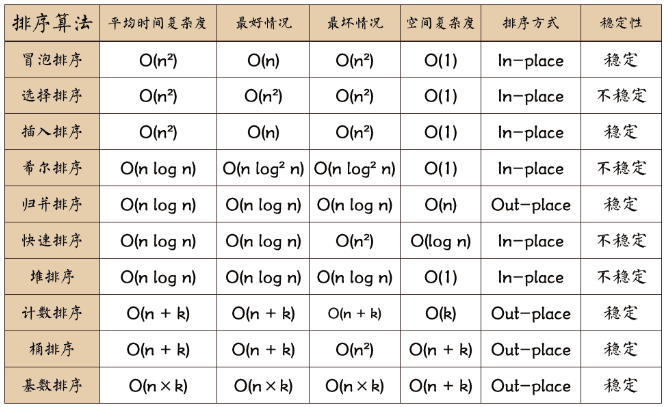
按照时间复杂度、稳定性、排序方式分为三个梯队
第三梯队选手：冒泡、选择、插入
平均时间复杂度都是\(O(n^2)\)
冒泡排序
思想
每次遍历交换相邻位置元素，遍历数组长度次
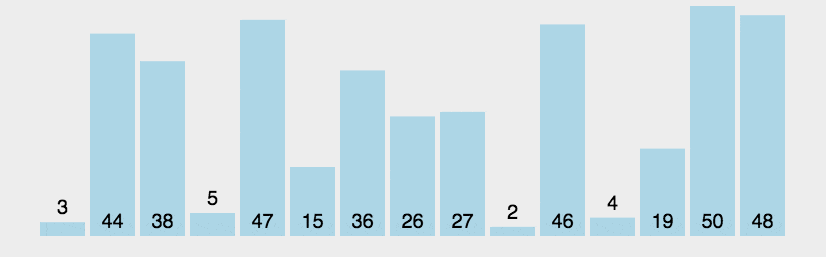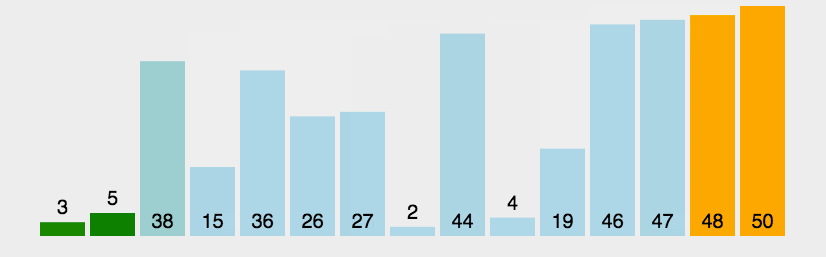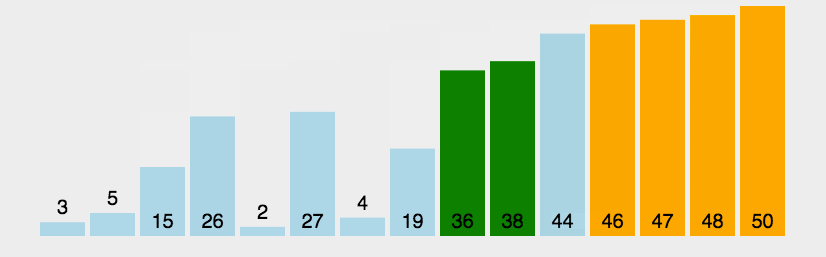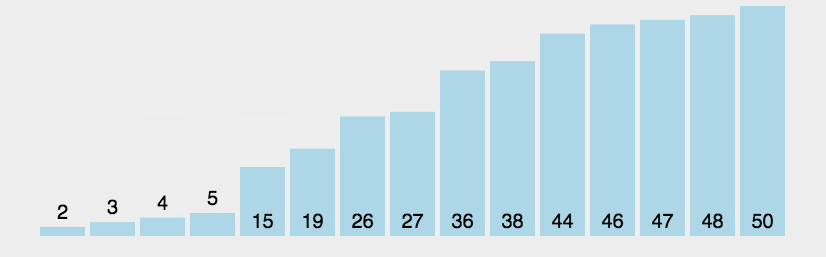
def bubblesort(nums):
for i in range(len(nums)):
for j in range(len(nums)-i-1):
if nums[j] > nums[j+1]:
nums[j],nums[j+1] = nums[j+1],nums[j]
return nums
复杂度
时间复杂度：\(O(N^2)\)
空间复杂度：\(O(1)\)
稳定性：稳定排序，排序后原数组中相同位置不会改变
选择排序
思想
每次遍历找到数组中最小（最大）的元素，逐次添加到新列表
def selectsort(nums):
sorted_nums = []
for i in range(len(nums)):
num = min(nums)
sorted_nums.append(num)
nums.remove(num)
return sorted_nums
上面的代码是选择排序的简单过程，使用了额外的存储空间，我们尝试不借用外部空间
def selectsort(nums):
for i in range(len(nums)):
minix = i
for j in range(i+1,len(nums)):#剩余无序数组
if nums[minix] > nums[j]:
minix = j
nums[i],nums[minix] = nums[minix],nums[i]#交换最小值到i位置，使i之前为有序
return nums
复杂度
时间复杂度：\(O(N^2)\)
空间复杂度：\(O(1)\)
稳定性：不稳定排序。如序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法
插入排序
思想
插入排序的过程就像打扑克时，将新牌插入到手牌，使之有序
两两比较，交换位置
def insertsort(nums):
for i in range(1,len(nums)):
for j in range(i-1,-1,-1):
if nums[j+1] < nums[j]:
nums[j],nums[j+1] = nums[j+1],nums[j]
return nums
直接插入有序区
def insertsort(nums):
for i in range(1,len(nums)):
insertvalue = nums[i]
j = i-1
while j>=0 and insertvalue < nums[j]:
nums[j+1] = nums[j]#复制有序区的值
j -= 1
nums[j+1] = insertvalue
return nums
复杂度
时间复杂度：\(O(N^2)\)
空间复杂度：\(O(1)\)
稳定性：稳定排序
下面有请第二梯队选手：希尔、归并、快排、堆排序
平均时间复杂度都是\(O(nlogn)\)
希尔排序
希尔排序是插入排序的一种更高效的改进版本，插入排序的两个特点：
- 大多数元素有序时，插入排序更快
- 元素数量较少时，插入排序更快
思想
将整个待排序序列划分为多个子序列进行插入排序
def shellsort(nums):
gap = len(nums)
while gap>0:
gap = gap//2
for i in range(gap,len(nums)): #插排
insertvalue = nums[i]
j = i
while j >= gap and nums[j-gap] > insertvalue:
nums[j] = nums[j-gap]#插入值小 互换元素
j -= gap
nums[j] = insertvalue
return nums
复杂度
时间复杂度：\(O(nlogn)\)
空间复杂度：\(O(1)\)
稳定性：非稳定排序
归并排序
思想
归并排序采用分而治之的思想，将原序列划分为子序列，再进行合并
def mergesort(nums):
if len(nums)<=1:
return nums
mid = len(nums)//2
l = mergesort(nums[:mid])
r= mergesort(nums[mid:])
return merge(l,r)
def merge(left,right):
result = []
p1,p2 = 0,0
while p1<len(left) and p2<len(right):
if left[p1] <= right[p2]:
result.append(left[p1])
p1 += 1
else:
result.append(right[p2])
p2 += 1
while p1 < len(left):
result.append(left[p1])
p1 += 1
while p2 < len(right):
result.append(right[p2])
p2 += 1
return result
复杂度
时间复杂度：\(O(nlogn)\)
空间复杂度：\(O(n)\),使用了额外的存储空间
稳定性：稳定排序
快速排序
思想
分而治之，选基准，比大小
def quicksort(nums):
if len(nums)<2:
return nums
pivot = divide(nums)
return quicksort(nums[:pivot])+quicksort(nums[pivot:])
def divide(nums):
pivot = 0
left,right = 0,len(nums)-1
while left < right:
while left<right and nums[right] >= nums[pivot]:#右端大于基准值，右指针左移
right -= 1
while left < right and nums[left] <= nums[pivot]:#左端大于基准值，左指针右移
left += 1
if left < right:
nums[left],nums[right] = nums[right],nums[left]#交换左右指针指向元素
nums[pivot],nums[left] = nums[left],nums[pivot]#将基准值换到中间位置
return left+1
这个看起来更简洁
def quicksort(nums):
if len(nums) <2:
return nums
pivot = nums[0]
left = [num for num in nums[1:] if num<=pivot]
right = [num for num in nums[1:] if num>pivot]
return quicksort(left)+[pivot]+quicksort(right)
时间复杂度：\(O(nlogn)\)
空间复杂度：最优空间复杂度：\(O(log(n))\)，递归深度，每次基准为中间元素；最差空间复杂度：\(O(n)\)，基准选最大（小）值，初始排列为逆序
稳定性：非稳定排序
堆排序
思想
利用堆的概念进行排序，循环创建堆，弹出堆顶元素
堆实现原地排序，堆创建可以参考创建堆(python)
def downadjust(nums,parentindex,length):
temp = nums[parentindex]
childindex = 2*parentindex + 1
while childindex < length:
if childindex +1 <length and nums[childindex+1] < nums[childindex]:#右孩子值小于左孩子，父节点和小的交换
childindex += 1
if temp < nums[childindex]: #父节点小于子节点，不用调整
break
nums[parentindex] = nums[childindex]
parentindex = childindex
childindex = childindex*2+1
nums[parentindex] = temp
def buildMinHeap(nums):
for i in range((len(nums)-1)//2,-1,-1):
downadjust(nums,i,len(nums))
def heapSort(nums):
#创建堆
buildMinHeap(nums)
#循环,堆顶元素和堆尾互换，产生新堆顶
for i in range(len(nums)-1,-1,-1):
nums[i],nums[0] = nums[0],nums[i]
downadjust(nums,0,i)
简洁实现(使用了额外空间)
def heapsort(nums):
import heapq
res = []
for i in range(len(nums)):
heapq.heapify(nums)
res.append(heapq.heappop(nums))
return res
官方实现（更简洁）
def heapsort(iterable):
h = []
for value in iterable:
heappush(h, value)
return [heappop(h) for i in range(len(h))]
复杂度
时间复杂度：\(O(nlogn)\)，建堆复杂度为\(O(nlogn)\)，下沉复杂度为\(O(logn)\)，循环\(n-1\)次，杂度为\(O(nlogn)\)，两次运算并列关系，总复杂度为\(O(nlogn)\)
空间复杂度：\(O(1)\)
稳定性：非稳定排序
下面有请第一梯队选手：计数、桶、基数排序
平均时间复杂度都是线性，并且都是稳定排序
计数排序
思想
将输入数据映射到额外数组，数组长度为输入数据的取值范围，利用数组下标确定元素位置
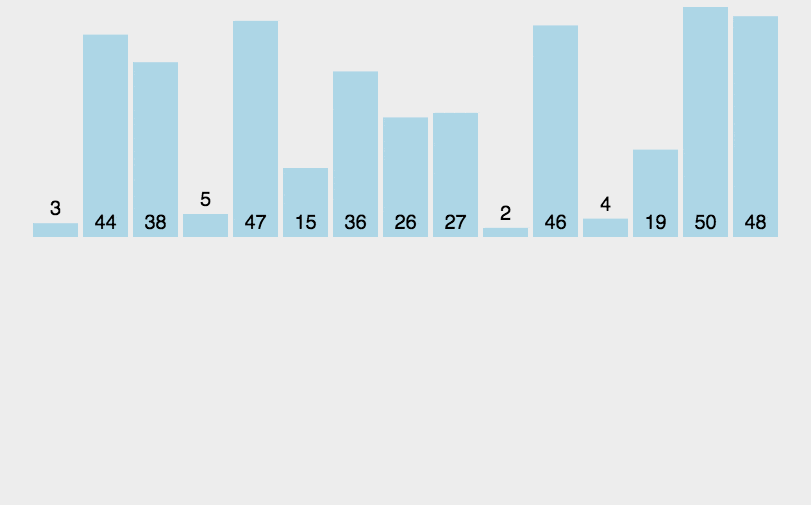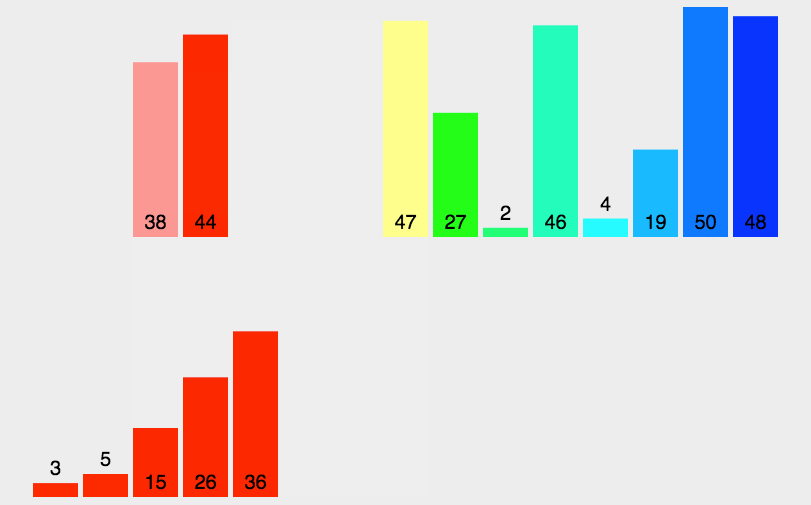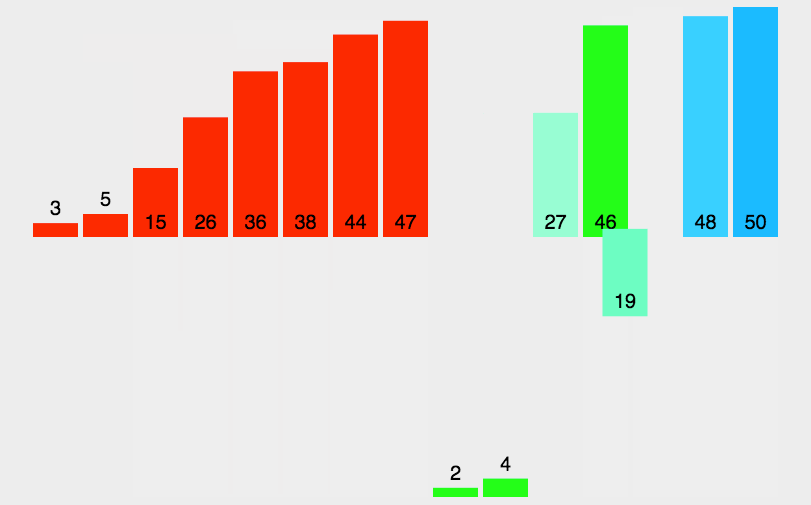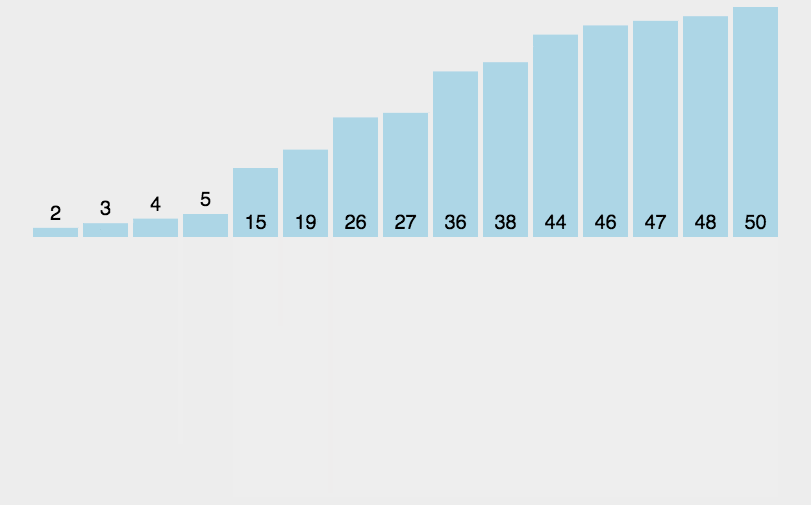
假设输入数据
9，3，5，4，9，1，2，7，8，1，3，6，5，3，4，0，10，9 ，7，9
取值范围在0-10，映射到额外数组，数组下标就是输入数据范围，下标对应的值为输入数据中该元素出现的次数
遍历数组，输出数组元素的下标值，元素的值是几，就输出几次：
0，1，1，2，3，3，3，4，4，5，5，6，7，7，8，9，9，9，9，10
显然，这个输出的数列已经是有序的了
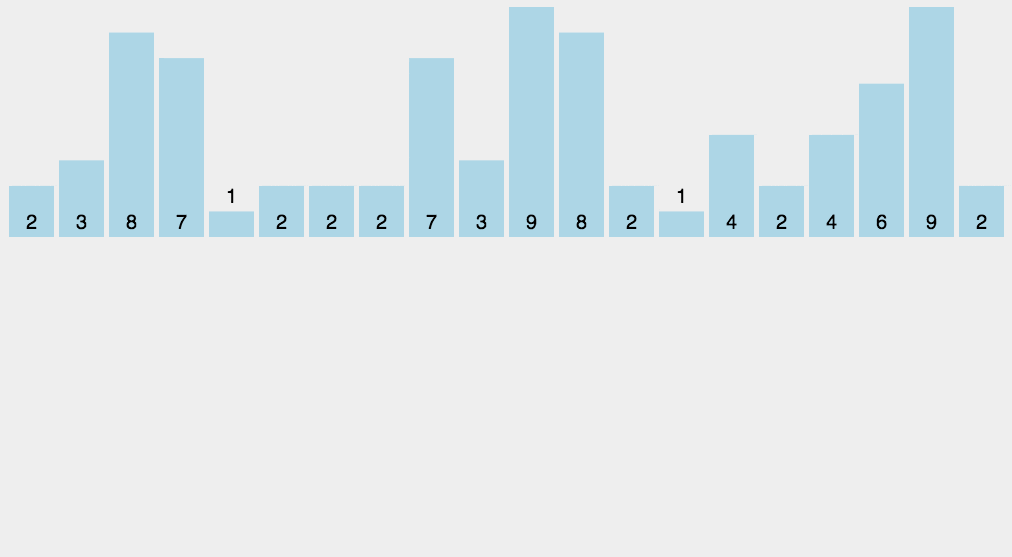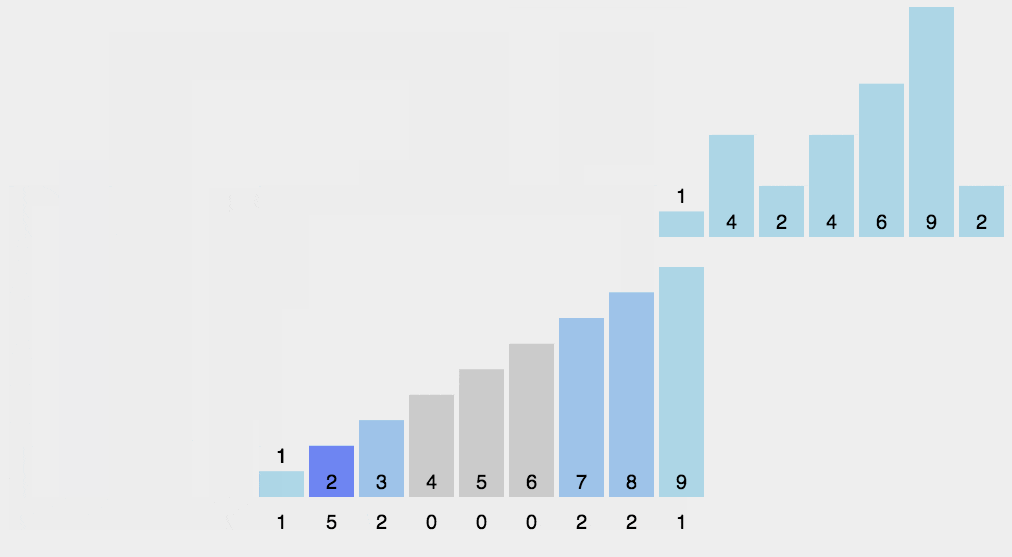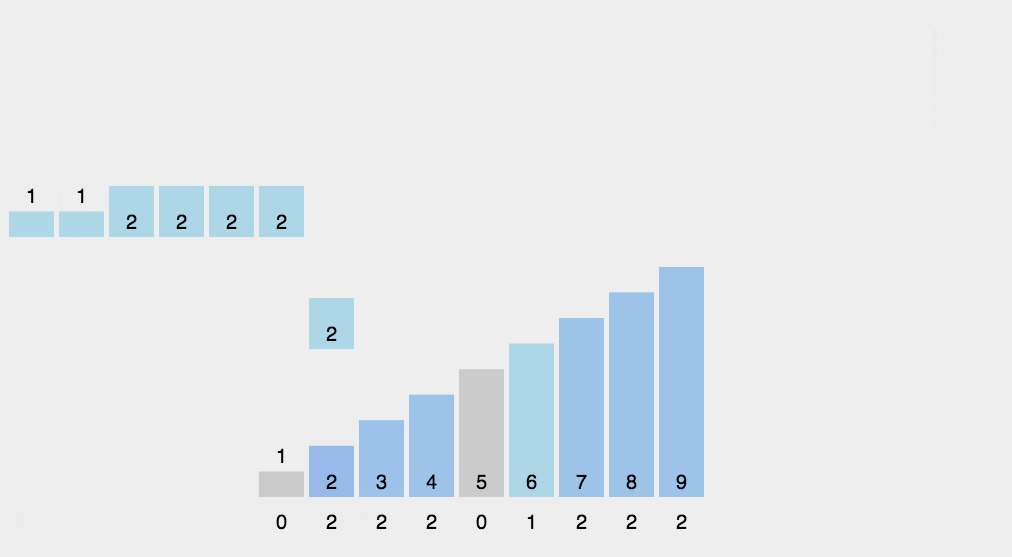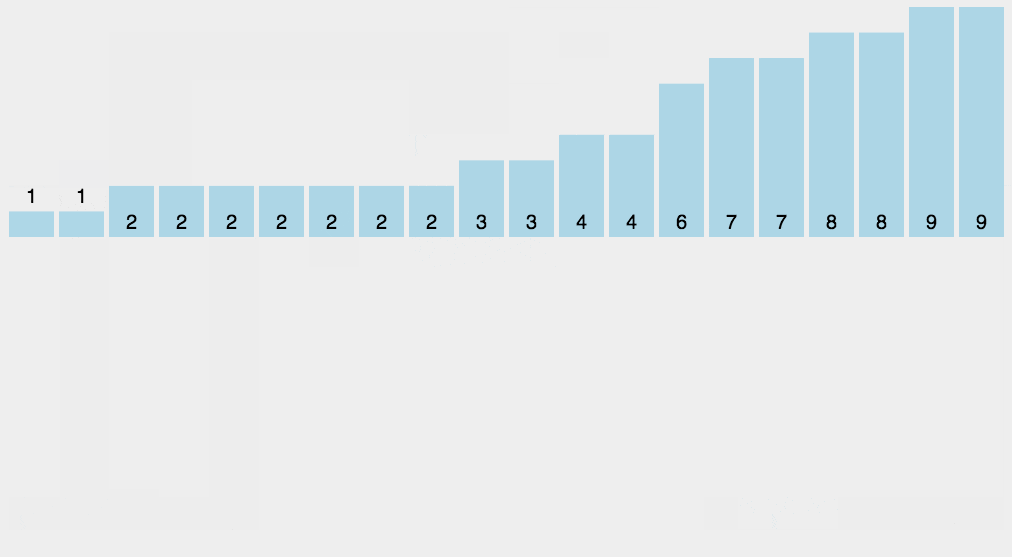
def countsort(nums):
#映射到额外数组
counts = [0]*(max(nums)+1)
for num in nums:
counts[num] += 1
#遍历输出结果
res = []
for i in range(len(counts)):
while counts[i]>0:
res.append(i)
counts[i] -= 1
return res
复杂度
时间复杂度：\(O(n+k)\),两个数组
空间复杂度：\(O(k)\)
稳定性：稳定排序
桶排序
思想
计数排序升级版，可以处理浮点型数据；每个桶代表区间范围
这里创建的桶数量等于原始数列的元素数量
def bucketsort(nums):
#初始化桶
buckets = [[] for _ in range(len(nums)+1)]
maxnum = max(nums)
minnum = min(nums)
#区间范围
bucket_range = (maxnum-minnum)/len(nums)
#元素入桶
for num in nums:
buckets[int((num-minnum)//bucket_range)].append(num)
#桶内部排序,遍历输出结果
res = []
for bucket in buckets:
for num in sorted(bucket):
res.append(num)
return res
复杂度
时间复杂度：\(O(n+k)\),两个数组
空间复杂度：\(O(n+k)\),空桶空间+桶中数列空间
稳定性：稳定排序
基数排序
思想
元素按位拆分，每一位进行一次计数排序的算法，就是基数排序
假设对长度为\(k\)的字符串排序：每一个轮只根据一个字符进行计数排序，一共排序\(k\)轮
下面代码实现字符串排序
def radixsort(nums,maxlen):
sorted_nums = [0]*len(nums)
#从低位到高位，逐次比较
for k in range(maxlen-1,-1,-1):
# 1.创建统计数组
count = [0]*(128+1) #ASCII_RANGE = 128
for i in range(len(nums)):
index = getCharIndex(nums[i],k)#获取第k位的ascii码序号
count[index] += 1
#统计数组做变形，后面的元素等于前面的元素之和
for i in range(len(count)):
count[i] = count[i] + count[i-1]
#倒序遍历
for i in range(len(nums)-1,-1,-1):
index = getCharIndex(nums[i],k)
sortedIndex = count[index]-1
sorted_nums[sortedIndex] = nums[i]
count[index] -= 1
#下一轮排序需要以上一轮的排序结果为基础，copy 结果
nums = sorted_nums[:]
return nums
def getCharIndex(s,k):
#如果字符串长度小于k，直接返回0，相当于给不存在的位置补0
if len(s)<(k+1):
return 0
return ord(s[k])
>>> nums = ["qd","abc","qwe","hhh","a","cws","ope"]
>>> radixsort(nums,3)
['a', 'abc', 'cws', 'hhh', 'ope', 'qd', 'qwe']
复杂度
时间复杂度：\(O(nk)\), \(k\)轮计数排序，\(O(k(m+n))\),\(m\)字符取值范围
空间复杂度：\(O(n+ m)\)
稳定性：稳定排序
排序算法就先学到这里了
