读吴恩达算-EM算法笔记
最近感觉对EM算法有一点遗忘，在表述的时候，还是有一点说不清，于是重新去看了这篇<CS229 Lecture notes>笔记. 于是有了这篇小札.
关于Jensen's inequality不等式:
Corollary(推论)：
如果函数f(x)为凸函数,那么在 f(x) 上任意两点X1,X2所作割线一定在这两点间的函数图象的上方，即：
举例子： 当t=1/2 ; 1/2*f(x1) + 1/2*f(x2) >= f( 1/2*x1 + 1/2*x2 );
或者我们直接抽象的表示为： E[f(X)] ≥ f(EX) ，其中E表示期望.
那么这个 Jensen's inequality（Jensen's 不等式在EM算法中起到什么作用呢？）这里我们先不表.
关于极大似然评估(MLE)：
假定存在一个样本集 D= {x1,x2,...,Xm },为M个独立分布的样本. 假设似然函数为: 联合概率密度函数P(D ; θ) ，其中(P(D ; θ)这种表示相当于P(D),只是存在未知参数θ)
我们知道了似然函数之后，将样本数据展开:
P(D ; θ) = p(x1,x2,...,Xm;θ) = ∏mi=1 p(xi ; θ)
我们令 L( Z ) = ∏mi=1 p(xi ; θ) ,如果存在θi 使得 L(θ)最大，我们认为θi为θ的极大似然估计量,同时我们认为θi(x1,x2,...,xm)为样本集D的极大似然函数估计量
关于求解极大似然函数：
求使得出现该组样本的概率最大的θ值。
θi = argmax(L(θ)) = argmax( ∏mi=1 p(xi ; θ) );
继续回到上面的公式：
L( θ ) = ∏mi=1 p(xi ; θ); 要使得L(θ)最大，那么对这个公式进一步化解：
等价于： log( L(θ) ) = log( ∏mi=1 p(xi ; θ) ) = ∑m i=1 P(xi ;θ)
(∑m i=1 P(xi ;θ))' = d( ∑m i=1 P(xi ;θ) ) / d(θ) =0 ; 求导 得 θ的解
关于极大似然求解的步骤：
（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数；
（4）解似然方程。
我们先来看文章给出的这样一个问题：
比如我们有一个训练集合X={ x1 , x2 , .... , Xm};里面包含M个样本. 我们希望将模型p(x，z)的参数与训练集合数据进行拟合，其中的函数-对数似然是:
我们想上面求解极大似然函数一样来求解这个似然函数：
对它进行微分方程，求导 d( L(θ) ) / d( θ ) =0; ？ 我们很快就发现无法求解，因为存在新的未知变量Z(隐变量)；如何来解释这个隐变量Z呢？
比如这样一个例子:
比如有A,B两个人比赛随机打靶，每个人每次打4枪，当命中九环以内，包括九环,是记录为1，否则记录为0; 但是由于裁判熬夜玩游戏，比赛完成是，收集比赛结果时，搞混了靶纸。于是整理出如下结果:
| 人名 | 结果 |
| 未知 | 1011 |
| 未知 | 0011 |
| 未知 | 1101 |
| 未知 | 0101 |
| 未知 | 1011 |
| 未知 | 0010 |
| 未知 | 1111 |
| 未知 | 1011 |
问A命中九环的概率pa，B命中九环的概率pb?
而这里的隐变量Z就是人名的顺序。
面对这个问题，显然使用极大似然函数去正面扛困难重重,EM算法为这个问题，提供了一个很好的思路：
求解分两步走：
E step 期望阶段：
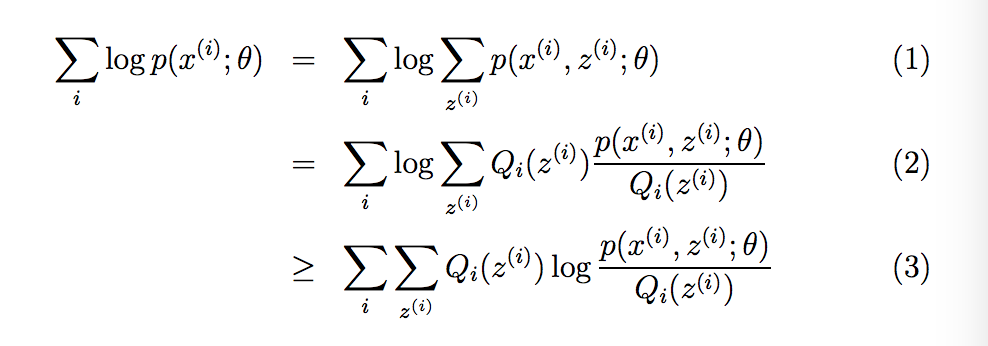
先假定，即初始化A,B命中的概率pa0=0.2 , pb0=0.5;
求出8次打靶中，该次打靶的结果是A,B的可能性即概率:
第一次打靶：如果是A的打靶结果： 0.2*0.8*0.2*0.2=0.0064
如果是B的打靶结果: 0.5^4 =0.0625
| 第i次打靶 | A | B |
| 1 | 0.0064 | 0.0625 |
| 2 | 0.0256 | 0.0625 |
| 3 | 0.0064 | 0.0625 |
| 4 | 0.0256 | 0.0625 |
| 5 | 0.0064 | 0.0625 |
| 6 | 0.1024 | 0.0625 |
| 7 | 0.0016 | 0.0625 |
| 8 | 0.0064 | 0.0625 |
如此，我们依据极大似然函数，来确定每一轮是谁打的
1轮: P(A1)<P(B1),
由上面这个表，我们在假定的前提下，计算出了A或者B的出现每轮打靶结果的概率；我们可以依据这个结果，进一步计算第i次是A,B打靶的相对概率
求出8次打靶中，该次打靶的结果是A,B的相对可能性即概率:
第一次打靶：如果是A的打靶结果： 0.0064/(0.0064 + 0.0625) =0.0928
如果是B的打靶结果: 0.0625/(0.0064 + 0.0625) =0.9072
| 第i次打靶 | A | B |
| 1 | 0.0928 | 0.9072 |
| 2 | 0.290 | 0.710 |
| 3 | 0.0928 | 0.9072 |
| 4 | 0.290 | 0.710 |
| 5 | 0.0928 | 0.9072 |
| 6 | 0.620 | 0.380 |
| 7 | 0.0249 | 0.9751 |
| 8 | 0.0928 | 0.9072 |
我们先假定A，B命中的概率pa1,pb1，然后去推到它们比赛的顺序，再依据比赛的顺序，来计算A,B命中的概率Pa2,pb2. 当pa2,pb2和pa1,pb2结果相差时较大时，
将pa2,pb2代入，继续推到它们的比赛顺序，计算A,B命中的概率
