N-gram的简单的介绍
目录：
1. 联合概率
2. 条件概率
3. N-gram的计算方式
4. 评估N-gram的模型.
前言：
N-gram是机器学习中NLP处理中的一个较为重要的语言模型，常用来做句子相似度比较，模糊查询，以及句子合理性，句子矫正等. 再系统的介绍N-gram前，我们先了解一下这几种概率.
正文：
1、联合概率介绍：
形如：p(W1,....,Wn); 表示的意思是： w1,...Wn同时发生的概率.列举一个具体的例子说明：
P(A,B) ,表示的是A,B同时发生的概率.
1.1 当A,B相互独立时，也就是交集为空的时候，P(A,B) = P(A)P(B)
1.2 当A,B相关联的时候，或者说存在交集的时候，P(A,B) = P(A)P(B|A),如下图所示
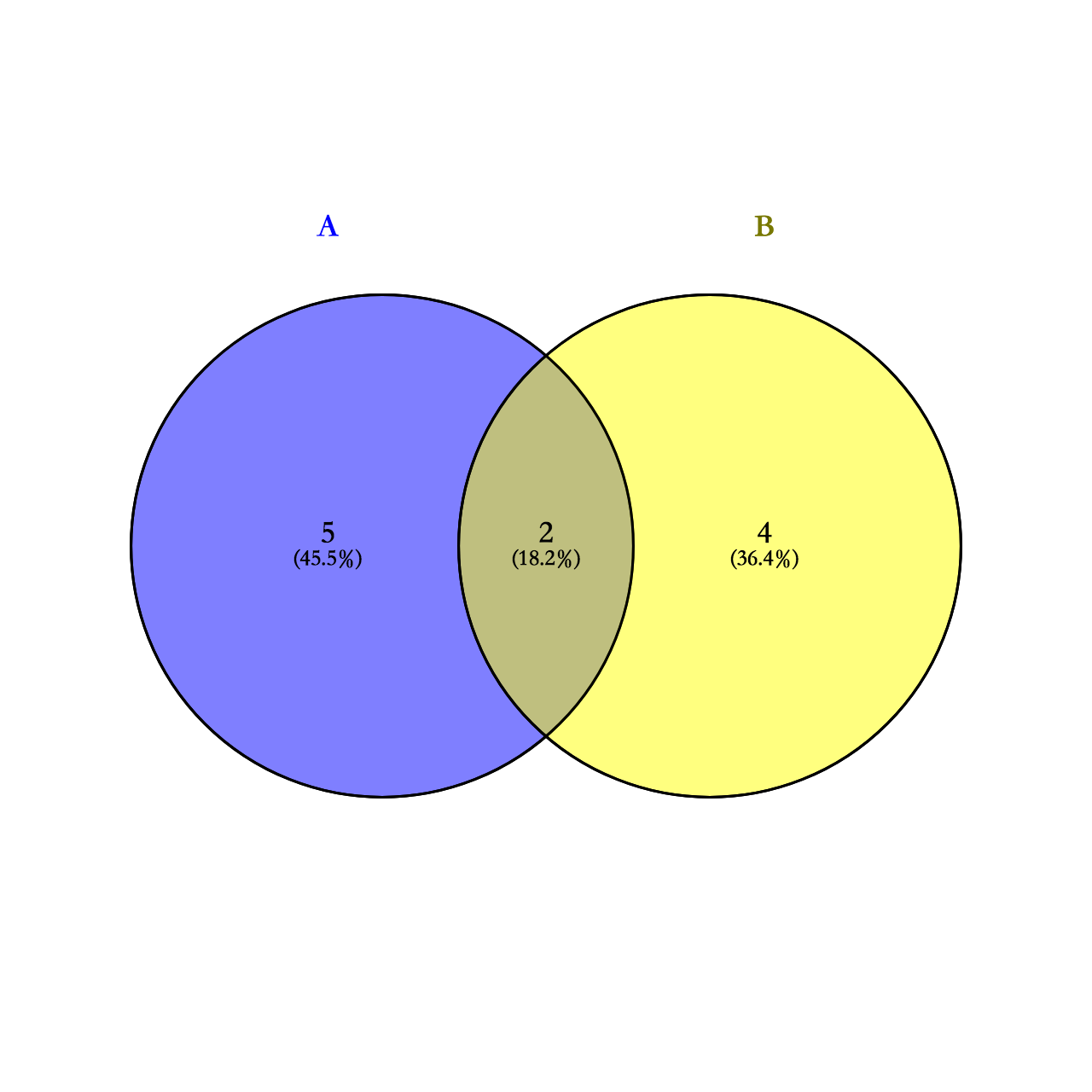
总的样本数为T，A的样本数为7，B的样本数为6，A,B相同的样本数为2
那么:
P(A,B) =2/T
1.3 1.2处的公式简化到一般形式：
P(w1,w2,w3) = P(W1)P(W2|W1)P(W3|W1,W2)
一般形式为： P(W1,W2,..,Wn) = P(W1)P(W2|W1)...(Wn|Wn-1,...,W2,W1);
抽象为：
P(W1,W2,...,Wn) = ∏ni P(wi|w1,w2,..wi-1) (累乘)
2、条件概率：
形如： P(A|B), 当某一系列事件放生时，该事件发生的概率.,如上图中的韦恩图所示：
P(A|B) = P(A,B)/P(A) = 2/7
我们将其扩展到一般形式：
P(A|B,C) = P(A,B,C) / P(B,C) = P(A,B,C) / ( P(B|C) P(C) )
3. N-gram的计算方式：
N-gram是依据一个预料库中，对于单词的统计，来计算. N-gram常见的有1-gram（一元模型），2-gram(二元模型) ,3-gram(三元模型);
在语义上只认为相近的几个词有关联 ,如果用韦恩图表示:
3.1 对于一元模型（1-gram）,每个词都是独立分布的，也就是对于P(A,B,C) 其中A,B,C互相之间没有交集. 所以P(A,B,C) = P(A)P(B)P(C)
比如语句：“猫，跳上，椅子” ，P(A="猫"，B="跳上"，C="椅子") = P("猫")P(“跳上”)P("椅子")；其中各个词的数量数语料库中统计的数量
| 猫 | 跳上 | 椅子 | |
| 13 | 16 | 23 |
依据这些数据就可以求出P(A,B,C),也就是这个句子的合理的概率.
P(A,B,C) = P(A)P(B)P(C) =13/M * 16/M * 23/M
3.2 对于二元模型，每个词都与它左边的最近的一个词有关联，也就是对于P(A,B,C) = P(A)P(B|A)P(C|B)
比如语句：“猫，跳上，椅子” ，P(A="猫"，B="跳上"，C="椅子") = P("猫")P(“跳上”|“猫”)P("椅子"|“跳上”)；其中各个词的数量数语料库中统计的数量
| 猫 | 跳上 | 椅子 | |
| 猫 | 0 | 9 | 1 |
| 跳上 | 0 | 3 | 15 |
| 椅子 | 0 | 0 | 0 |
依据这些图表一和图表二就可以求出P(A,B,C),也就是这个句子的合理的概率.
P(A,B,C) = P(A)P(B|A)P(C|B)
p(A) = 13/M
P(B|A) =9/13
p(C|B) = 15/16
3.3 对于三元模型，每个词都与它左边的最近的两个词有关联. 计算同上.
4. 评估模型的优劣
对于一个训练好的模型，我们需要评估模型的好坏，N-gram常用的评估方式是：
pp(w1,w2,...,Wn) = p(w1,w2,...,Wn)-1/n
我们以上面的一元模型和二元模型来为例，进行评估计算.
pp(w1,w2,...,Wn)1 = (13/M * 16/M * 23/M)-1/3 = (12*16*23)-1/3*M 一元模型
pp(w1,w2,...,Wn)2 = （13/M * 9/13 * 15/ 16）-1/3 = (9*15/(16M))-1/3 二元模型
可以看出二元模型比一元模型的值要小，而值越小说明模型越好.
