面试高频：双指针---6题14图一次搞懂

使用双指针是降低算法复杂度的一个有效途径，有些问题的暴力解法时间复杂度是O(n^2)，但使用双指针可以大幅度降低算法复杂度。如果面试者能将求解过程从暴力法优化到双指针，说明面试者的基础知识、代码能力、逻辑思维都是十分扎实的。

同贪心算法一样，双指针的难点在于自己想不出、别人的理解不了、正确性难以证明。

常用的双指针法有一下几类：

1. 左右指针：两个指针，相向而走，中间相遇。
2. 快慢指针：两个指针，有快有慢，同向而行。
3. 灵活运用：两个指针，灵活运用，伺机而动。

下面将结合具体题目，从暴力做法一步一步优化到双指针，攻克想不出、看不懂、不会用的难题。

左右指针

左右指针地熟练使用需要一定经验的积累，如果接触的较少，是不容易想出来的。下面将以题目为例，一步步从暴力解法优化到双指针。

思路：先找出暴力解法，根据题目性质，优化到双指针

例题一:盛最多水的容器

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点(i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为(i, ai)和(i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

 

 

示例 ：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

这道题的最优解法是左右双指针法。双指针法的难点在于难于想到，难以证明。接下来将一步一步地从暴力解法优化到双指针法。证明也就很简单了。

暴力法：

找出每一种情况，求出盛水值，最大的就是答案。

1. i指向左挡板，从第一块到遍历倒数第二块。

2. j指向右挡板，从倒数第一块遍历到i后面那一块。

3. res保存最大盛水值。

4. 返回res。

代码：

//cpp
class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.size() <= 1) return 0;
        int res = 0;//保存结果
        for(int i = 0; i < height.size() - 1; i++)//以i为左挡板，从O开始
        {
            for(int j = height.size() - 1; j > i; j--)//以j为右挡板，从height.size() - 1开始
            {
                int L = j - i;//底边长度
                int H = min(height[i], height[j]);//对短的挡板为高
                res = max(res, L * H);//取最大值
            }
        }
        return res;
    }
};

 

用S[l,r]表示以第l块板为左挡板，第r块板为右挡板的盛水值。S[l, r]就等于min(height[l], height[r]) / (r - l)。

以输入[1,8,6,2,5,4,8,3,7]为例，共8块挡板，看看都计算了哪些值：

 

 

 

 

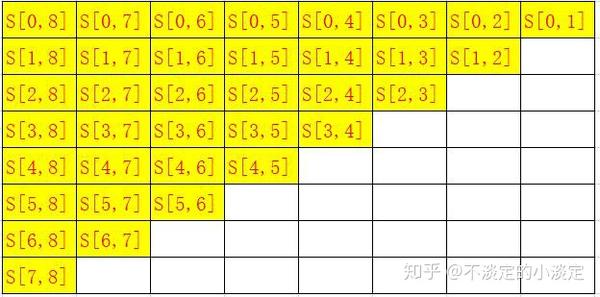
优化：

1. 开始时，l指向第0块挡板，r指最后一块挡板。S[l, r]=min(1, 7) * (8 - 0) = 8。

 

 

 

 

 

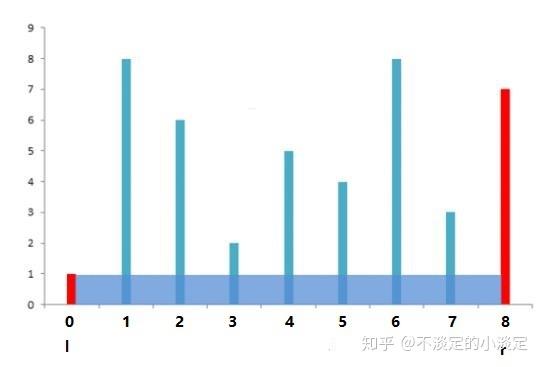
2. 向内移动指向较长挡板的r指针，盛水面积不会变大。向内移动r指针的时候，盛水值S[l, r] = min(height[l], height[r]) / (r - l)。min(height[l], height[r]) 不会大于height[l]，也就是不会大于7。(r - l)会随着r内移减小。所以向内移动r指针的时候,盛水值不可能变大。也就是S[0,8]肯定大于S[0,7],S[0,6],S[0,5],S[0,4],S[0,3],S[0,2],S[0,1]。

因此知道了以height[0]为左挡板的最大盛水值。以后计算就不用考虑height[0]了

 

 

 

 

 

3. 子问题就变成了：在[8,6,2,5,4,8,3,7]中求出最大盛水值，然后与刚才的求出的以height[0]为左挡板的最大盛水值比较大小，大的为答案。

 

 

 

 

 

4. 子问题求解时，用l指向指向第0块挡板，也就是height[1]，r指最后一块挡板,也就是height[8]。S[l, r]=min(8, 7) / (8 - 1) = 56。

这个时候，如果向内移动指向较长挡板的l指针，盛水面积不会变大。

因为向内移动l指针的时候，盛水值S[l, r] = min(height[l], height[r]) / (r - l)。min(height[l], height[r]) 不会大于height[r]，也就是不会大于7。(r - l)会随着l内移减小。所以向内移动l指针的时候,盛水值不可能变大。也就是S[1,8]肯定大于S[2,8],S[3,8],S[4,8],S[5,8],S[6,8],S[7,8]，就知道了以height[8]为右挡板的最大盛水值。

 

 

 

 

 

 

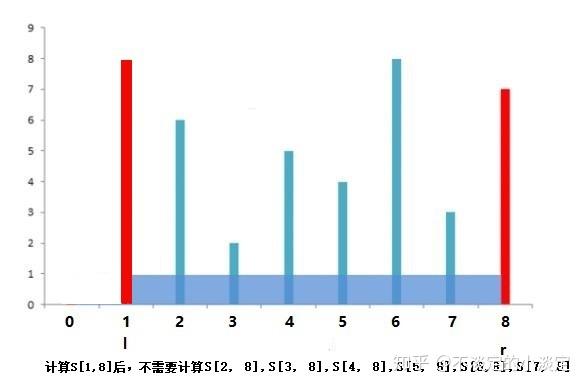
5. 子问题可以再次缩小，就变成了：在[8,6,2,5,4,8,3]中求出最大盛水值，然后与刚才的求出的以height[0]为左挡板的最大盛水值，以height[8]为右挡板的最大盛水值比较大小，大的为答案。

6. 以此类推，每次就能求出以最外侧两个挡板中，短的挡板为边界的最大值。然后再一次缩小问题。就不需要计算所有的情况了，只需要计算出每块挡板为边界的最大值，然后求出其中的最大值，就是答案。

7. 这样下去，求解空间就变为了：

 

 

 

 

 

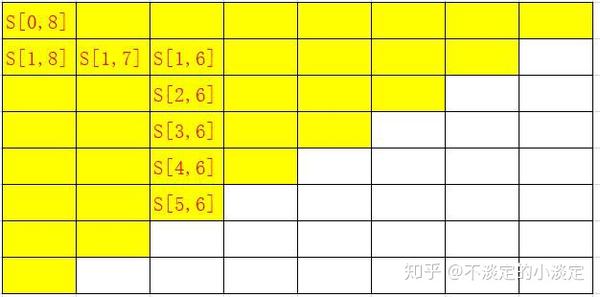
代码:

//cpp
class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.size() <= 1) return 0;
        int res = 0;//保存答案
        int l = 0, r = height.size() - 1;//开始时，l指向最左边的挡板，r指向最右边的挡板
        while(l < r)//如果l,r之间还有挡板
        {
            res = max(min(height[l], height[r]) * (r - l), res);//计算盛水值
            if(height[l] <= height [r])//谁小谁以后就不用再考虑 
                l++;
            else
                r--;
        }
        return res;
    }
};

时间上，l,r指针遍历一遍，所以时间复杂度是O(n)。空间上，没有开辟与输入有关的空间，所以空间复杂度是O(1)。

 

https://zhuanlan.zhihu.com/p/335817266