组合数学之方格路径

一个简单的问题

问从一个横边长为m，竖边长为n方格棋盘的一个角走到对角点的最短路径共有多少种方法？这个问题应该会有很多人见到过，想明白的话这也是一个很简单的问题，但是如果在这个问题上进行一点小小的改变，这个问题也是可以很有意思的。

level 0

方便起见就不失一般性的假设棋盘大小是4*3：
那么问题就是从左下角到右上角的路经数目有多少？
一种思路就是用动态规划的思想，到格子（i，j）处的只有两种方法：从（i-1，j）向右走一步或者从（i，j-1）处向上走一步。用N（i，j）表示从起点到（i，j）的路径数，则：

N（i，j）=N（i-1，j）+N（i，j-1）

所以这个3*4的棋盘问题可解：
动态规划解法

 

 

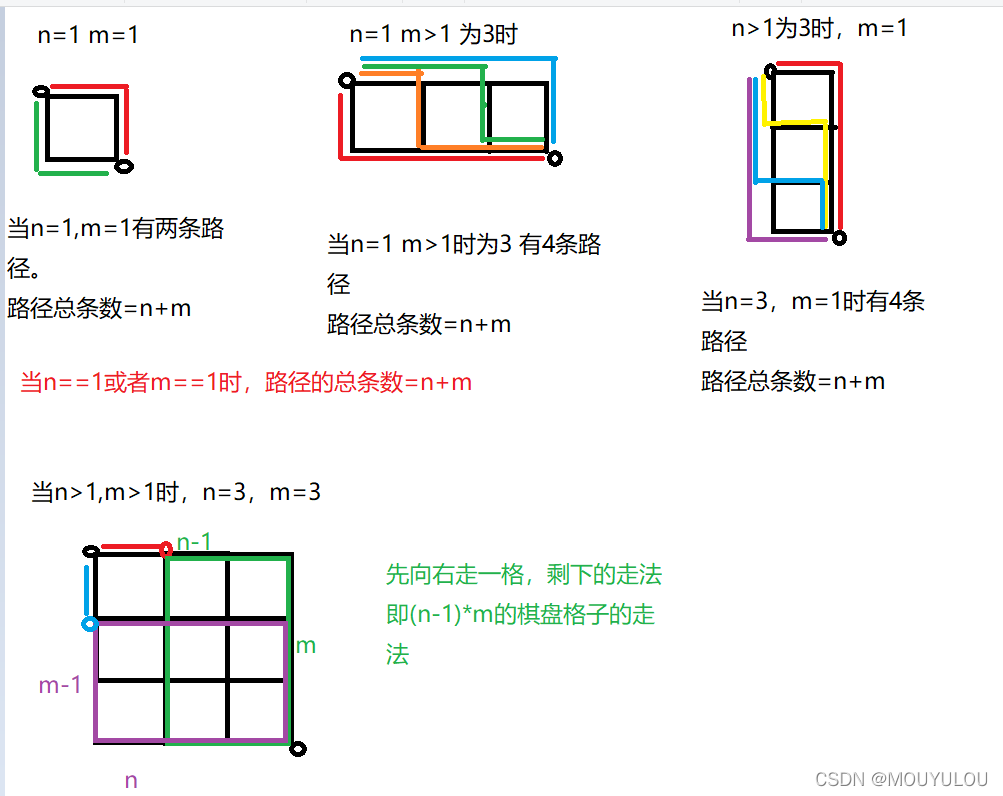
但是说的高大上是动态规划算法，说的不好听了不就是傻算嘛……换一个角度考虑就能转化成一个高中就能瞬间写出答案的问题，其实就是一种选择的问题。因为在每个路口都要做出选择，是向上还是向右走。就好像我高中骑车上学一样。假设我家在左下角（0，0），学校在右上角（4，3）。那么我可以先向右骑一段路，到路口（1，0），我可以选择向东直行到（2，0）或者左拐到（1， 1）处，每一个路口都要做出选择，但是全程我必须也只能向北走三段路，同理向东走四段路，即在全程长为7的路程中选择三段路向北走，四段路向东走。
例如（U U R U R R R ）或者（R U R U R U R）或者（R R R R U U U）都是可能的路径。（U表示向上走，R表示向右走）。
所以总路程数就是：

C(7,3) = C(7,4) = 35

同理从（0，0）点走到（m，n）处的路线数就是C（m+n，n）或者C（m+n，m）。  

 

最短路径一共的m+n步，我也不知道第一步怎么走，所有先排列，但是排列是有顺序的，所以要除以各自的顺序 （排列相当于单独开吃饭选菜，组合是拼桌吃饭选菜）

C(7,3) = C(7,4)  = A(m+n, n) / A(n,n) = A(m+n, m) / A(m,m) = (P(m+n)/P(n)) / P(m) = P(m+n)/P(n)*P(m)

 

4×3网格，从左下角A点到右上角B点，每次只能向上或者向右走一步，不重复的最短路径有多少条？（如图所示）

 

中学的同学，可以使用排列组合来完成这道题，我们考察下图，

 

通过对上图的观察，我们不难发现，最短的走法, 都由七步组成，其中向上走了三次，向右走了四次，从而得出，其总数是：

 

 

小学同学可能还没学过排列组合，通常会用一种标格子的办法来解决。到某一个点的走法总数实际上是到它的左边相邻点的走法总数，与到它的下边相邻点的走法总数之和，另外到边界上的各点走法总数都是 1。

具体请看下面这个图：

 

实际上，这样的思路在编程时非常有用,可以通过递归不断减小问题的规模，最终求出答案。根据上面的思路我们可以写出下面的递归公式：

根据上面的递归公式 

35

学习Python的同学，可以得出这样的代码。

def f(x ,y) :

if x == 0 or y == 0 :

return 1

else :

return f(x-1, y) + f(x, y-1)

f(4,3);;

　　

35

以上代码的程序的执行过程，可以用下面的树形图表示出来：

 

为了简明起见，上图求的是 f(3,2) , 也就 10。同学们可以注意到树形图的叶子结点数，即是计算的结果 10。

此外，使用程序，我们很容易列举其中所有的走法。

其基本思想是，到某处的所有走法，可以用如下方法获得：

1.在其左边的格子的所有走法的后面加上一个'右

2.在其下边的格子的所有走法的后面加上一个'上

3.将1. 2.的结果合并起来 

学习Python的同学可以这样写：

def f(x,y) :

if x == 0 and y==0 :

return [[]]

else :

r = []

if x > 0 : r += [v + ['右'] for vin f( x-1 , y )]

if y > 0 : r += [v + ['上'] for vin f( x , y-1 )]

return r

for v in f(4,3):

print(v)

['上', '上', '上', '右', '右', '右', '右']

['上', '上', '右', '上', '右', '右', '右']

['上', '右', '上', '上', '右', '右', '右']

['右', '上', '上', '上', '右', '右', '右']

['上', '上', '右', '右', '上', '右', '右']

['上', '右', '上', '右', '上', '右', '右']

['右', '上', '上', '右', '上', '右', '右']

['上', '右', '右', '上', '上', '右', '右']

['右', '上', '右', '上', '上', '右', '右']

['右', '右', '上', '上', '上', '右', '右']

['上', '上', '右', '右', '右', '上', '右']

['上', '右', '上', '右', '右', '上', '右']

['右', '上', '上', '右', '右', '上', '右']

['上', '右', '右', '上', '右', '上', '右']

['右', '上', '右', '上', '右', '上', '右']

['右', '右', '上', '上', '右', '上', '右']

['上', '右', '右', '右', '上', '上', '右']

['右', '上', '右', '右', '上', '上', '右']

['右', '右', '上', '右', '上', '上', '右']

['右', '右', '右', '上', '上', '上', '右']

['上', '上', '右', '右', '右', '右', '上']

['上', '右', '上', '右', '右', '右', '上']

['右', '上', '上', '右', '右', '右', '上']

['上', '右', '右', '上', '右', '右', '上']

['右', '上', '右', '上', '右', '右', '上']

['右', '右', '上', '上', '右', '右', '上']

['上', '右', '右', '右', '上', '右', '上']

['右', '上', '右', '右', '上', '右', '上']

['右', '右', '上', '右', '上', '右', '上']

['右', '右', '右', '上', '上', '右', '上']

['上', '右', '右', '右', '右', '上', '上']

['右', '上', '右', '右', '右', '上', '上']

['右', '右', '上', '右', '右', '上', '上']

['右', '右', '右', '上', '右', '上', '上']

['右', '右', '右', '右', '上', '上', '上']

　　

细心的同学，可能会发现，计算步数的公式和杨辉三角形的公式是一样的。还没看出来的同学，可以参考一下下面这个图哦。

 

 

参考：

https://zhuanlan.zhihu.com/p/580756466