函数式编程和Data Parallel：MapReduce的前前前世

由于一时心血来潮、想针对谷歌三驾马车(MapReduce, GFS, BigTable)分别写点啥，故我上个月在Google File System及其继任者Colossus中针对以GFS为代表的谷歌存储系统写了一篇日志。而这次，以三者中最出名的MapReduce为展开点，让我们随便谈谈相关的有趣东西。

不同于作为单独组件存在的GFS和BigTable，MapReduce是一个分布式计算框架，即，在MapReduce的帮助下，开发者仅需少量简单的代码就能有效地利用成百上千台机器对PB级的数据进行分析、处理，并对可能出现的错误拥有良好的抵抗能力。从前，分布式/并行计算通常是令人望而却步的领域(例如HPC)，而MapReduce的出现则将入门要求大幅降低，让我们每个人都有过把瘾的机会。正是因为如此，MapReduce在Big Data大行其道的当下红得发紫，其开源实现Hadoop也成为各类公司的标配，提出者Jeff Dean更是由此封神(好吧他本来就是神)。

不过在开始说MapReduce之前，我打算先谈谈其他看似不太相关的话题——函数式编程。

函数式编程(Functional Programming)

不知道大家在刚开始学编程的时候，是否有为(或身边人为)编程语言的不直观疑惑不解：

int x=0;
x=x+1;

这个 x=x+1实在是让从幼儿园开始就学数学的我们犯懵：等式两边约掉 x，难道意味着 1=0么？

当然，我们后来都知道，这里的等号意味着“赋值”。由于我们所用到的语言一般而言是命令式编程语言(Imperative Programming)，即“用命令的方式告诉计算机每一步该做啥”(当然这也是图灵机的基本运作方式，现在处理器的工作模式)，所以这一步“将 x加一，结果赋值给 x”作为命令也就不难理解了。然而，有更符合我们最初设想的类似数学逻辑的编程方式么？答案是肯定的。

声明式编程(Declarative Programming)正是这样一种方式。开发者通过描述问题的定义和问题和问题之间的关系，让计算机知道如何求得最终解。函数式编程是声明式编程的一种，其初衷在于，让编程看上去像数学上定义函数 f(x)=x+1一样，“优雅”地写程序。

一瞥Haskell

说到函数式编程，就不得不提到Haskell，一种“纯粹的”函数式编程语言。在Haskell的世界里，没有变量，一切皆为函数(常数为接受0个参数的常值函数)，而最终问题则由已经定义的各种函数组合而成。由于没有变量，也就是没有全局状态，所有需要记录的状态均在参数中体现，函数的运行结果自然也只和输入参数相关。Talk is useless，让我们看看Haskell实现快速排序的代码吧：

qsort [] = [] 
qsort (x:xs) = qsort [y | y <- xs, y <= x] ++ [x] ++ qsort [y | y <- xs, y > x]

是的，仅用两行就结束了.... 乍一看，这恍若天书的代码令人无法理解，但如果我们回想快排的数学递归定义 (假设x为列表，x0为列表的第一个元素，x'为剩余元素组成的列表，*为连缀列表操作)

 

f(x)={}(x_is_empty)�(�)={}(�_��_�����)
f(x)=f({y|y∈x′,y≤x0})∗x0∗f({y|y∈x′,y>x0})(otherwise)�(�)=�({�|�∈�′,�≤�0})∗�0∗�({�|�∈�′,�>�0})(��ℎ������)

 

不难发现，Haskell对快排的描述，和其数学定义几乎完全一致，这正是Haskell作为编程语言的精彩之处。当然，Haskell编程并非本文要点，再讲下去恐有偏题之嫌，如果有兴趣的小伙伴可以自学一下Haskell或Scala。

Python和Lambda表达式

Python借鉴函数式编程的思想，原生支持了Lambda表达式：Lambda表达式本身如同常量值一般可以赋值给任何变量，但同时也可以作为函数调用；另外，Lambda表达式对应了函数式编程思想里的“纯函数”：没有变量、不会改变全局状态、所有状态均在参数体现、函数输出仅仅由参数决定。例如，

plus_one=lambda x:x+1
print plus_one(1)        # 2

在这基础上，一些“函数的函数”则格外有趣。它们接受一个数列和一个函数，并做出若干计算后输出一个新的数列。由于在函数式编程中它们被使用的非常频繁，故被放在Python builtin包中，不用import任何依赖即可使用。它们是 map、 filter和 reduce，其定义可按以下代码理解：

# 将list中每个元素用func作用一遍，并输出结果数列
def map(func, list):            
    res=[]
    for i in list:
        res.append(func(i))
    return res
# 将list中每个元素用func作用一遍，输出结果为true的元素
def filter(func, list):            
    res=[]
    for i in list:
        if func(i):
            res.append(i)
    return res
# func为二元函数，对list的每个元素以init和该元素为参数计算新的init
def reduce(func, list, init):    
    for i in list:
        init=func(init, i)
    return init

这几个看似平凡的函数可以方便地完成很多任务：

# 连缀两个数列 (相当于 x + y)
concat=lambda x, y: reduce(lambda l, e: append(l, e), y, x)

# 快速排序 (和Haskell逻辑完全一致)
quicksort=lambda x: [] if len(x)==0 else quicksort(filter(lambda z: z<=x[0], x[1:])) + [x[0]] + quicksort(filter(lambda z: z>x[0], x[1:]))

# 取最大值(非负整数)
max=lambda x: reduce(lambda p, q: p if p>=q else q, x, 0)

# 求和
sum=lambda x: reduce(lambda p, q: p+q, x, 0)

读到这里，读者也许会觉得这不过是普通的语法糖而已。从功效上看，Python对函数式的编程的支持和语法糖区别不大,但值得注意的是其中所代表的函数式思想。一言以蔽之，函数式思想中的函数有如下几个特征：(可以看到，均和数学函数一致)

  • 无副作用：除了输出结果，函数的运行不能对外界产生任何影响。
  • 确定性：对于确定的输入，函数的输出总是某个可以确定的值。
  • 显性定义的数据关联：任何相关联的数据均由函数关联，除此外的数据互相独立；特别的，一个列表中的元素相互独立。

Data Parallel

那么上述函数式思想对分布式/并行计算有什么帮助呢？这里我们需要提到三种主流的分布式系统下通信模型：共享内存(Shared Memory)、消息传递(Message Passing)和Data Parallel。对于前两种模型想必读者并不陌生：多线程并行所代表的Shared Memory、多机器并行时约定的网络通信协议对应的Message Passing，都十分常见直观。相较而言Data Parallel就显得较为晦涩：该模型通过将需要处理的输入数据分为互相独立的若干部分，来允许不同计算资源在互相几乎不通信/同步的情况下分别运行程序处理其中一部分。由于不同部分间相互独立，计算资源间的通信开销极低，分布式计算的加速效果在这种模型下最佳。

Data Parallel模型的一个典型代表是GPU编程，如CUDA。由于高端的GPU拥有上千核心，能同时处理上万并行线程，在该线程规模下，巨大的同步开销和race condition让共享内存和消息传递模型不再是很好的选择，而Data Parallel则脱颖而出。例如，CUDA中不同Thread Block间几乎完全独立，如果开发者能够对问题/数据进行很好的划分并采用Data Parallel模型编写程序，该问题在GPU上的执行效率就会远远高于CPU。

更一般地说，Data Parallel的模型非常类似于函数式编程思想中的 map函数。上文提到，在函数式编程中，一个列表的元素相互独立，且函数是确定、无副作用的，这完美地满足了Data Parallel的要求。故对于 map(func, list)，我们可以通过将 list分割到不同处理资源并同时运行 func来高并发地解决问题，如下图所示：

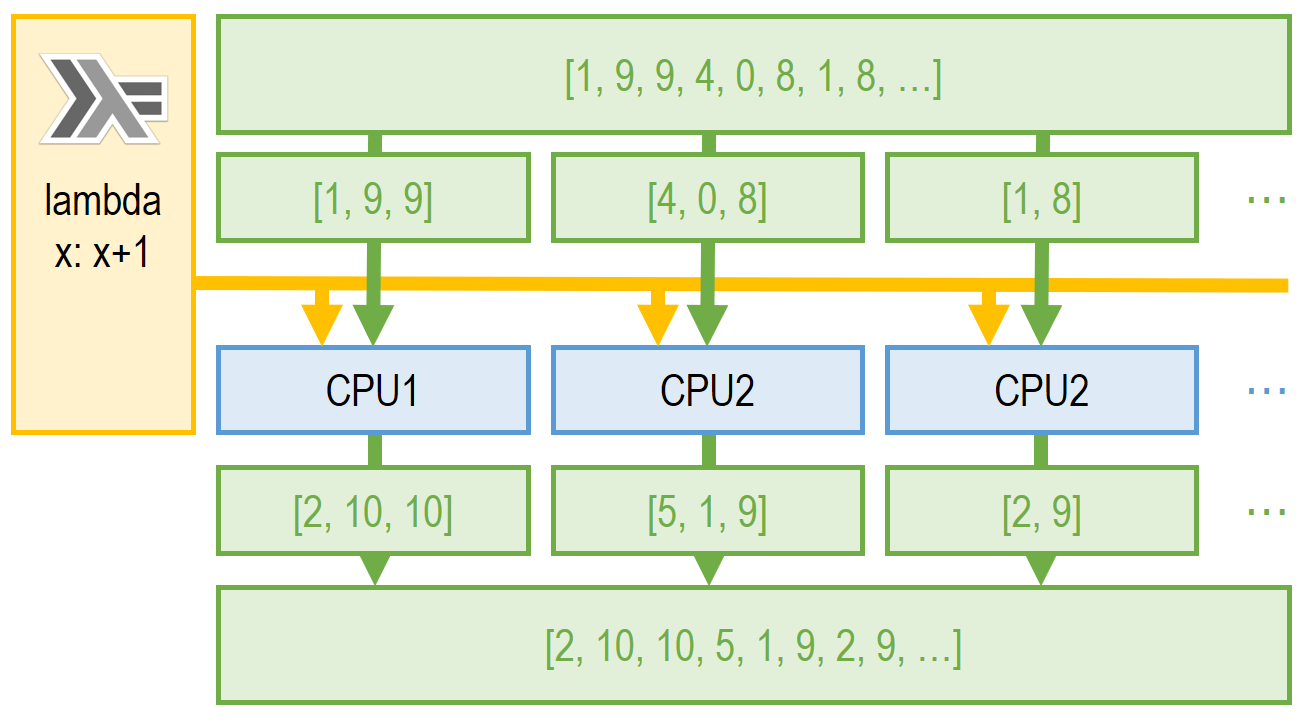
Data Parallel给我们提供了一个分布式计算的新思路：一个分布式计算框架并不需要兼顾所有类型的问题，相反，通过着眼于其中一类问题(例如存在函数式性质的问题)、并提供优秀的解决方案，而该类问题又恰巧满足了大量开发者的需求，该框架便有价值。在这样的启发下，MapReduce诞生了。

MapReudce

MapReduce吸纳了Data Parallel的优势，提出了如下两个核心函数：

  • Mapper：类似上文所述的 map函数中的 func参数，该函数会被作用于数据列表上的每一个元素，其必须满足函数式性质。不同的是，函数式编程中的 func输出可以是任何类型的值，MapReduce中mapper函数的输出一定是 (Key, Value)二元组；另外，一个mapper函数可以输出不止一个二元组。
  • Reducer：作用类似上文 reduce函数中的 func参数，该函数会被作用在Mapper函数处理原数据后的生成的二元组数列上。Reducer和上文的 reduce函数区别在于：1、对于一个数列，reducer并不会被反复调用迭代计算最终值，相反，reducer会一次性接受数列的全部数据并自行决定如何输出。2、reducer所作用的数列并非完整数据集，而是二元组中 Key相同的全部元组所组成的某个子数列。

整个MapReduce执行逻辑，用Python模拟如下：

from itertools import groupby

# mapper/reducer为函数，data为list
def MyMapReduce(mapper, reducer, data):    
    # 假设data=[1,2,3,4], mapper=lambda x: [(x,x), (x,x+1)], reducer=lambda (k, v):sum(list(v))

    data=map(mapper, data)    
    # data=[[(1,1),(1,2)], [(2,2),(2,3)], [(3,3),(3,4)], [(4,4),(4,5)]]

    data=reduce(lambda x, y:x+y, data, [])    
    # data=[(1,1),(1,2),(2,2),(2,3),(3,3),(3,4),(4,4),(4,5)]

    data=[(k, list(g)) for k, g in groupby(sorted(data, key=lambda t:t[0]), lambda t:t[0])]    
    # data=[(1, [1,2]), (2, [2,3]), (3, [3,4]), (4, [4,5])]

    return map(reducer, data)    # [3, 5, 7, 9]

从以上模拟代码可以看到，MapReduce所规定的数据模型紧紧地将计算限制在Mapper和Reducer两个用户自定义函数下——事实上，大部分常见算法均需要经过仔细的修改后才能在MapReduce框架下顺利运行(而这一修改过程造就了一大堆paper，毕业了一群phd。当然，这都是题外话了)。不过对于谷歌，这并不要紧，作为初创公司的谷歌只要能够将其看家绝活PageRank以及各种业务流程成功实现在MapReduce上，该框架便可用。所幸，事实正是如此，无论是网页DOM解析还是Page Rank，都能较好地放在MapReduce框架下运行。

回到最开始的问题，MapReduce通过限制计算模型实现了其最大的亮点：不需要开发者参与就自动实现的高并发(可扩展)、高容错性。那么这一点是如何实现、又和Data Parallel联系何在呢？

首先是高并发性和可扩展性。通过对模拟代码再次分析，我们可以得到如下几个并行点：

  • Mapper函数作用于输入数据的过程：该过程是典型的Data Parallel，在数据规模足够大时几乎可以完美扩展到任意大的集群上并达到理想的并发度。该步骤被称为map phase，执行该phase的机器称为mapper结点。
  • 对中间结果(元组list)排序和执行groupby对不同key分类：该步骤并不由开发者编写代码执行，而由框架自动实现。在group时，每台机器首先明确负责一部分key并从存储中间结果的机器收集和该key相关的元组，该步骤称为shuffle stage；而后，对于每个key，负责的机器将收集到的和该key有关的元组在本机排序，该步骤称为sort stage。
  • 对于每个key，以上参与sort和shuffle步骤的负责机器运行最后一行的map，将reducer函数作用于排序、合并好的中间结果并得到最终输出。由于对每个key，整个流程均在某一台机器执行，该步骤和sort, shuffle合称为reduce phase，执行该phase的机器称为reducer结点。

可以看到，map phase的可扩展性非常高，而reduce phase的可扩展性受限于key的数目和元组在key中分布的均匀性。优秀的MapReduce开发者会精心设计算法来产生合适数目的key并使得元组尽量均匀分布。

Map phase中Data Parallel所需要的数据分割任务由GFS/HDFS完成：在之前的日志中我们了解到，GFS已经将数据分割为Chunks存储在不同机器上，那么不难想到，遵循这样的分割、在该机器上用mapper函数处理该chunk已经是一个不错的方案。默认情况下，MapReduce中的Master结点会把一个GFS Chunk视为Data Parallel模型中的一个分割(Split)，将Mapper函数传输给容纳该chunk的机器完成map task。

当所有Map task完成后，Reducer结点会从所有Mapper结点的本地硬盘拿到和自己负责的Key有关的中间结果，通过网络传输回来后继续进行排序并喂给reducer函数。是为一个reduce task。

整个MapReduce在分布式环境下的运行流程如下：(图片来源: CMU 15-719 Advanced Cloud Computing讲义，转载请务必指明出处)

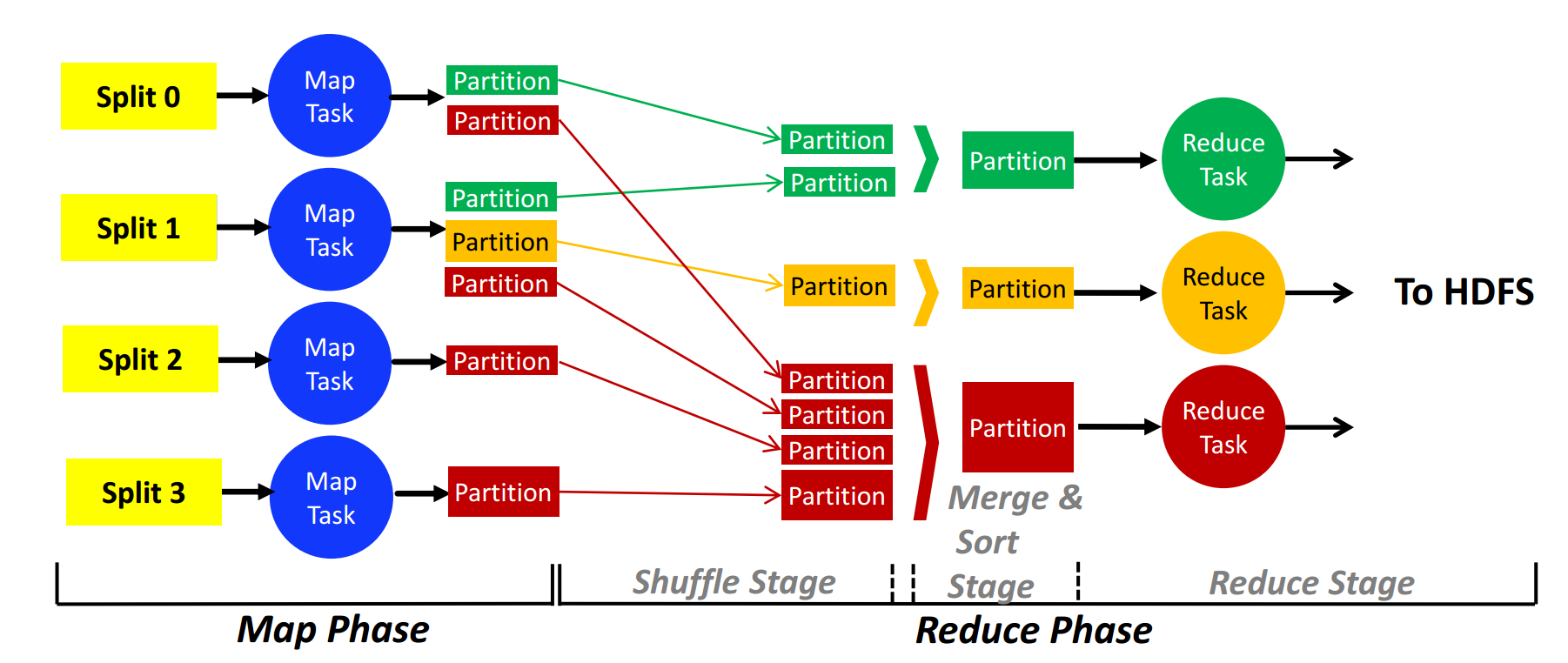
接下来我们再谈一下MapReduce的容错性实现方式。上图值得我们注意的一点是，对于任意一个stage，不同并行执行的task完全独立，即任意一个任务的失败不影响其他任务的顺利完成。考虑到该特性，对于常见的某机器挂掉、计算失败(如遇到异常)和数据丢失等错误，MapReduce的应对方式如下：

  • 数据丢失：GFS通过副本(Replication)处理了该问题，我们可以假设MapReduce不会遇到这类错误。
  • 计算结点死亡：该节点因为严重硬件问题或网络问题失去联系，那么正在该节点进行的map/reduce task和存储在该节点的中间结果全部丢失，且无法找回。所幸mapper和reducer函数均满足函数性语义，无副作用且有确定性，Master仅需将对应的map/reduce任务重新交给其他机器执行即可恢复进度。
  • 计算失败：因为各种各样的原因(用户程序的bug、资源不足等)，该节点无法完成被指定的任务。尽管如此，进行该计算的机器和MapReduce框架并没失去响应。在这种情况下，对应的机器会向Master报告该错误，Master着手将失败的任务安排在其他结点上。
  • Master死亡：这是由MapReduce的Master-Slave架构带来的特殊错误。和GFS一样，该系统对Master死亡缺乏处理能力，但该事件发生概率很小。

可以看到，MapReduce拥有在常见错误下良好的自我恢复能力，而该容错性也正是建立在廉价硬件集群上的大规模分布式计算所必不可少的(参见GFS)。

读到这里，认识到原理上的可行性，读者脑海中应该对MapReduce的架构、调度方式有简略的想法了。本文也就到此为止。关于实现上的细节，有兴趣的朋友可以找来Jeff Dean的论文本体或各仔细分析其实现的技术博客一探究竟，甚至可以关注开源的Hadoop源代码。毕竟系统这个东西，设计是一回事，实现起来又是另一个完全不同的故事了。

总结

我们从函数式编程出发，通过Haskell和Python，大致梳理了在函数式编程的概念下的计算应该满足的重要性质，并将该性质应用在并行计算领域、引出了重要的并行通信模型Data Parallel。受此启发，MapReduce通过限制待解决问题的类型、将复杂的数据处理任务抽象为mapper/reducer两个关键函数的方式保证了计算的高并发、高可扩展和容错性。

MapReduce仍然拥有诸多缺点，如计算模型过分拘泥于map/reduce跷跷板似的迭代、所有中间结果需要保存硬盘或GFS上等。针对这些缺点，UC Berkeley推出了新的Spark计算系统，将计算模型表示为更普适的有向无环图，用上真正的函数式编程语言Scala简化表达，并把中间结果存在内存中，最终大获成功。另外，Spark和Alluxio针对函数式计算的确定性和无副作用性，提出用Lineage(而非副本)进行容错的思想，又是一个新的有趣话题。

尽管相较于各类后起之秀，MapReduce已经显得比较naive，Google内部也推出了新一代继承系统作为替代，但不能否认的是，在MapReduce公开于世的十几年后的今天，该系统仍然显得不过时。不知道在21世纪初，当这个叫Google的创业公司实现该原型系统时，是否预料到它即将给分布式计算和数据分析领域带来的难以想象的深远影响呢。致敬Jeff。

参考文献

  • Dean, Jeffrey, and Sanjay Ghemawat. "MapReduce: simplified data processing on large clusters." Communications of the ACM 51.1 (2008): 107-113.
  • 清华大学本科生课程：函数式编程，周旻，孙家广
  • 15-719 Advanced Cloud Computing, Garth Gibson, Sakr Majd and Greg Ganger, Carnegie Mellon University
  • 15-618 Parallel Computer Architecture and Programming, Kayvon Fatahalian and Randy Bryant, Carnegie Mellon University
posted @ 2023-01-29 10:09  易先讯  阅读(30)  评论(0)  编辑  收藏  举报