多目标规划专题
多目标规划
一.例题分析
组合投资问题
设有8种投资选择:5支股票、2种债券、黄金。投资者收集到这些投资项目的年收益率的历史数据(见下表)。投资者应如何分配他的投资资金?即需要确定这8种投资的最佳投资分配比例。
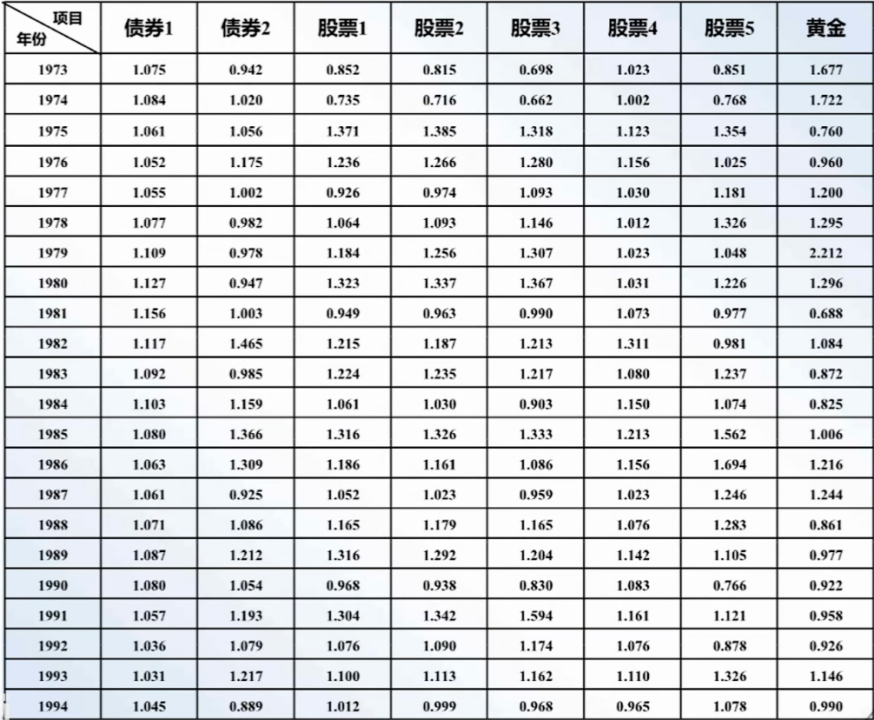
问题分析
首先,我们由多种指标,我们的目标是找到选择各指标的具体情况和最后总收益的关系,这样才能进一步分析最优投资策略。
我们已知各个指标的历史数据,第一步要做的就是根据历史数据得到一些描述该指标情况的具体参数,具体操作如下


法,评测某个特定的投资策略的具体收益情况,如下:
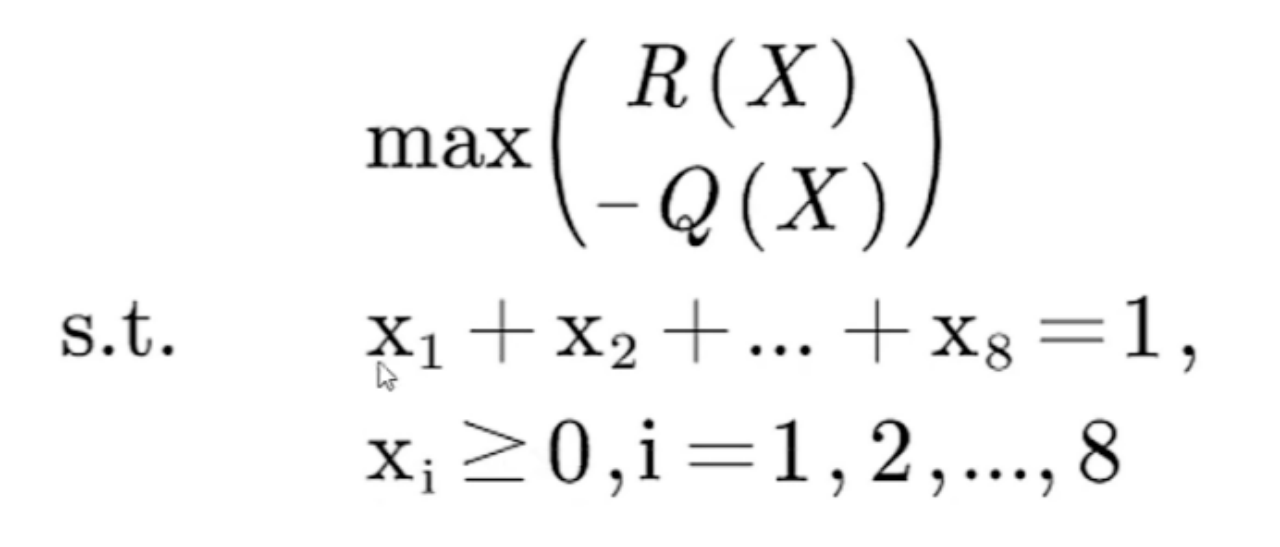
轻松的分析出规划模型的目标和约束,很明显越大化利润,最小海风险就是目标,如下
对于此类问题,有多种处理方法,最常用的是先尽可能把多目标规划转化为单目标规划,再对非线性规划进行处理
打个比方,有以下几种多目标转化为单目标的方法:


这样便把多目标规划转换成了单目标规划,再对单目标非线性规划问题进行求解。
matlab求解非线性规划问题主要用到以下函数:
fgoalattain 多目标规划
fminbnd 有界标量非线性优化问题
fmincon 约束非线性极小化 *
fminimax 极小极大最优化
fminsearch和fminunc 无约束非线性最优化 *
fseminf 半无限极小化
linprog 线性规划 *
quadprog二次规划 *
拿fminsearch和fminunc 为例,求解无约束非线性规划问题:
[X,fval ] =fminune(fun',x0,options)
[X,fval ] =fminsearch('fun',x0,options)
皆为“以x0为初始值求fun最小值”的问题,数学形式均为min fun(x),多元参数全部打包在x向量中,其中若fun是多参量函数,则x0是一个向量,更详细的问题可以去读matlab文档,这个工具箱的汉化整挺好,点赞
进一步的,对于有约束的问题而言,我们用fmincon函数求解
fmincon的数学形式为:
min f(X) (s.t. G1(X)<=0,G2(X)=0,A1X<=b1,A2X=b2,L<X<R)
调用形式[X,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@con),别忘了用方括号补齐缺项
如果目标函数不是线性的,而是二次的,我们就需要用quadprog进行求解
数学形式如下:
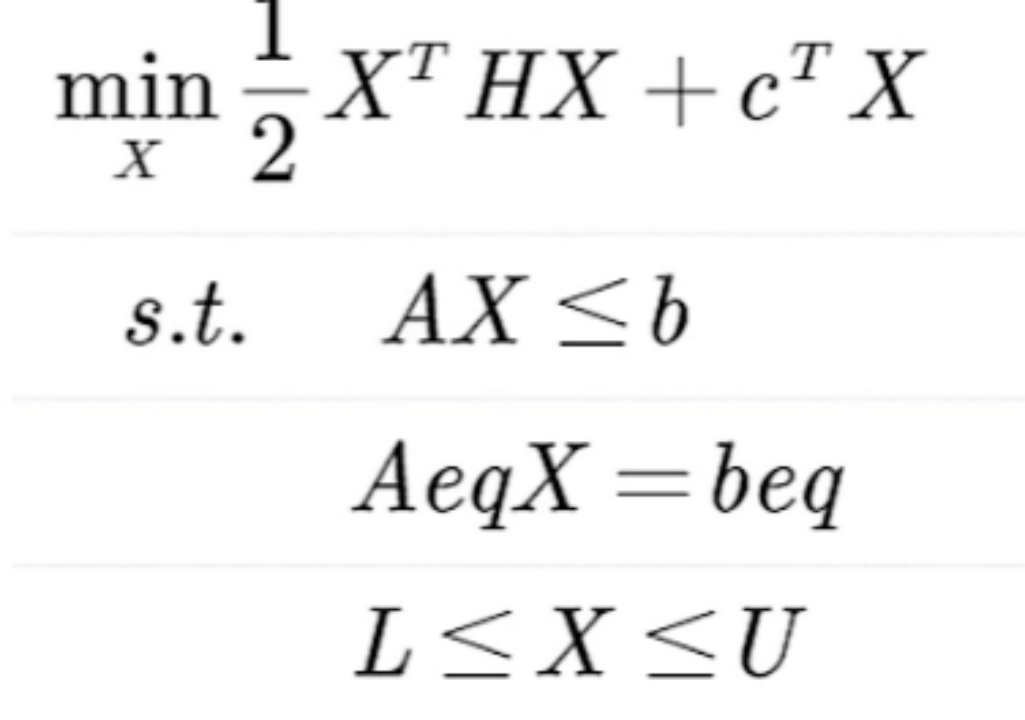
调用形式如下:
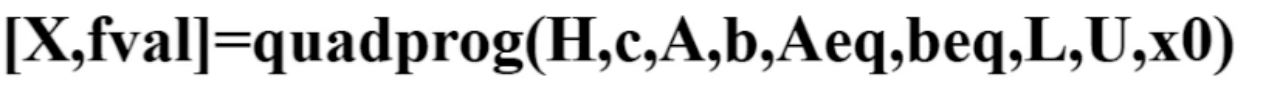
还可以把非线性规划转化为线性规划后用linprog进行求解
拿下面这个非线性规划问题为例:
6个建筑工地水泥的日用量分别为3、5、4、7、6、11吨,两个临时料场A、B,日储量各有20吨,假设从料场到工地均有直线相连。
问题1:试制定每天A、B两料场向各工地供应水泥的供应计划,使总的吨千米数最小。
问题2:为进一步减少吨千米数,打算舍弃两个临时料场,改建两个新的,日储量仍各为20吨,问应该建在何处,节省的吨千米数有多大?
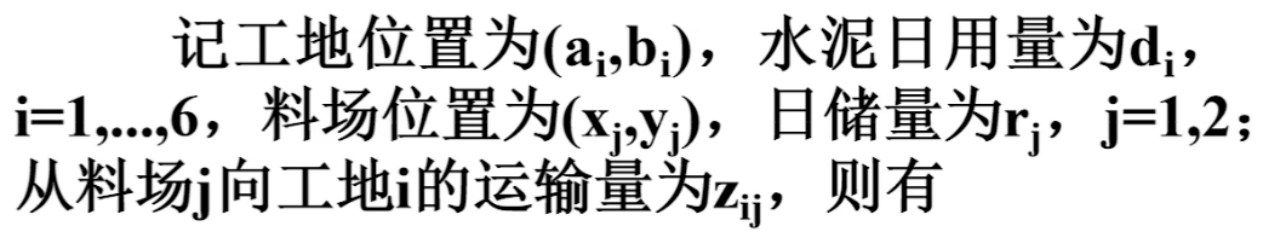
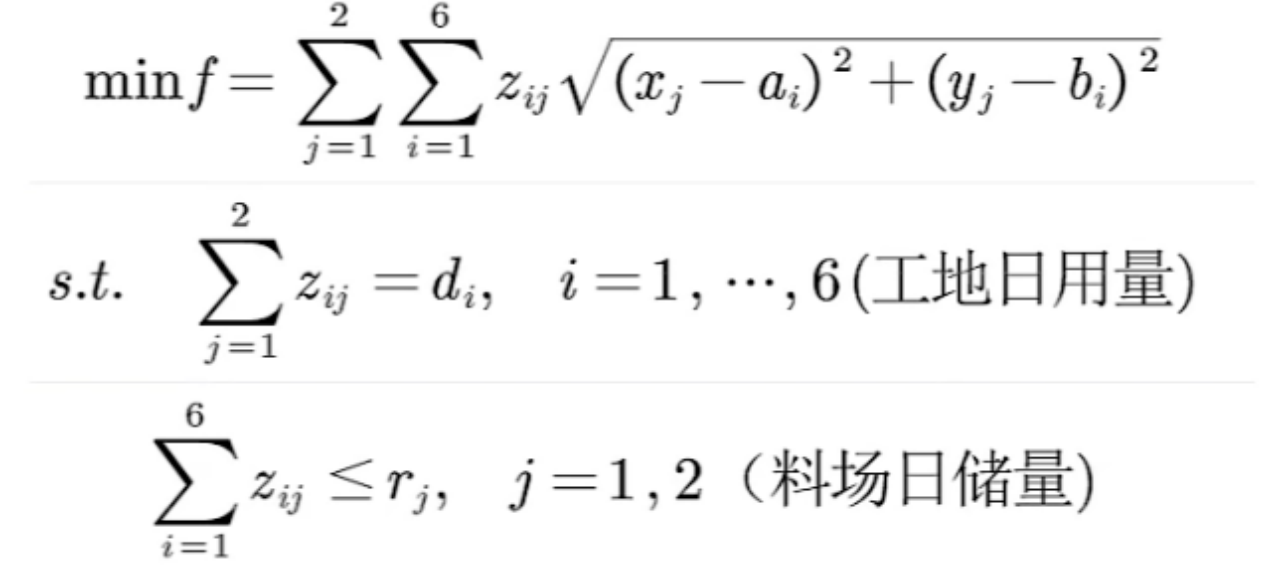
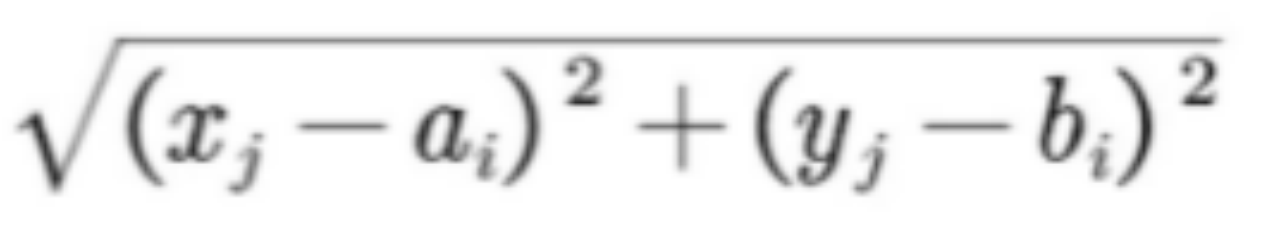
对于问题1,xy是绑定的自变量,对于每一组xy而言,我们都可以求出一个数cj与这组xy对应,其中ci=
然后直接把ci构成的向量C的值作为自变量的取值向量,将问题转化为线性规划问题,然后利用linprog求解,具体代码如下

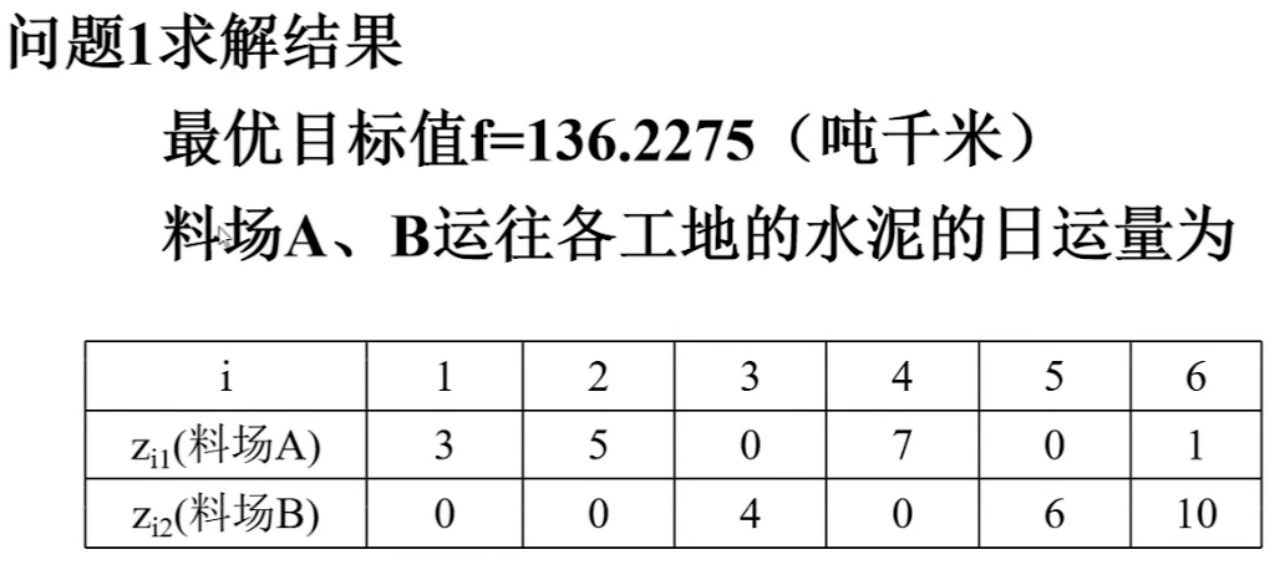
对于问题2而言,xy不再是绑定的,但还是可以用唯一的ci代替由唯一的一对xy确定的
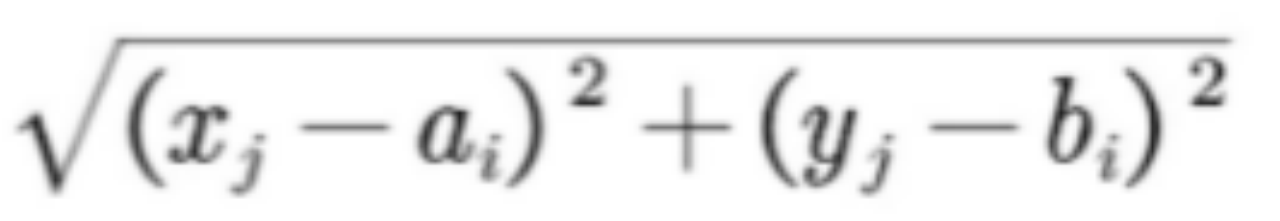
我们还是先给出两个给定xy组的目标函数,

设x是一个16维变量,存储了两个料场的坐标和各工地日运量,这样这个函数便可以返回这两个料场对应的目标函数值,以向量的形式无损返回
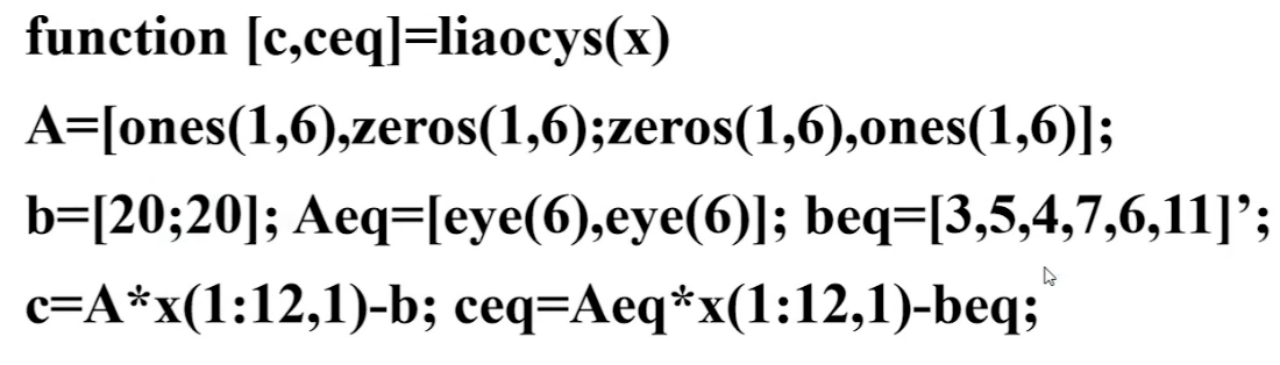

mincon进行求解
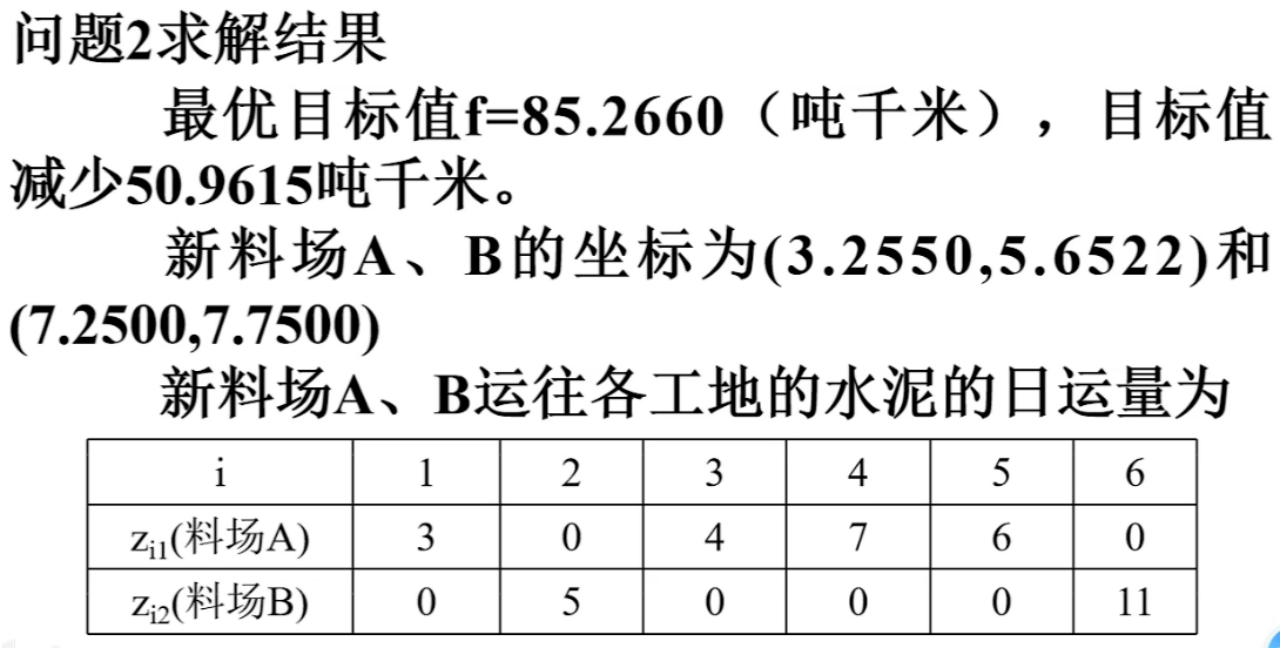

最后,我们抽象的表述一下多目标规划模型
一般的,定义向量如何算“min”是主观的,一般直接按权重分配,比如线性加权或均方加权,或者功效系数法,如下

不难想到fgoalattain的用法,该函数的数学形式如下:
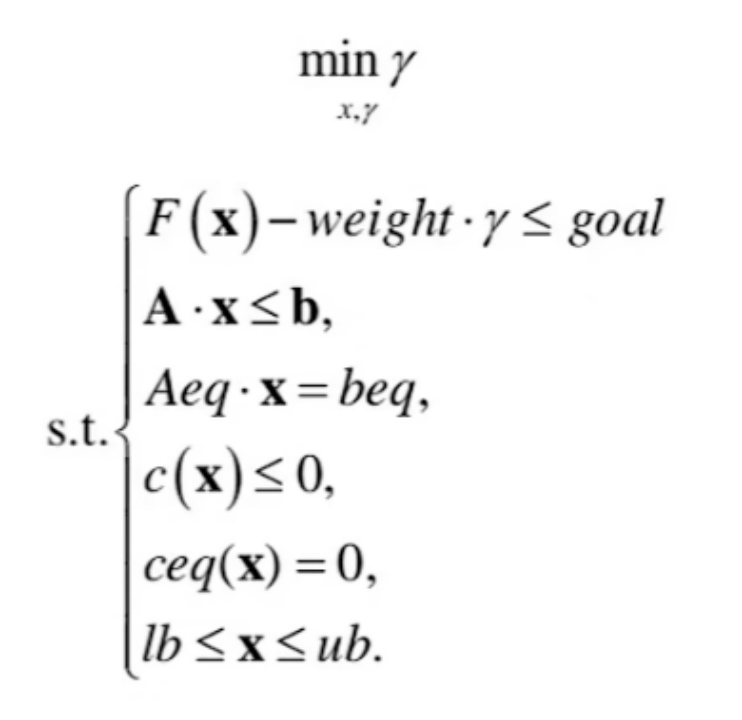
具体应用见matlab文档。

再拿一道题为例:


代码如下
那么进一步的,在我们已知适应度函数的基础上,总可以用以上方法解决问题,那如果我们不知道适应度函数呢?如果我们已知多因素影响下某一个或多个相应变量的一大组具体的对应关系,询问因素具体是怎么影响响应变量的,也就是反求他们的“适应度函数”或者说求回归曲线?那又该怎么办呢?
这样最优类问题就转换成了评价类问题,或者说大数据类问题,具体例题有国赛2021B和美赛2023C,从现在开始才算是真正开始上强度,见《回归分析专题》



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)
· AI 智能体引爆开源社区「GitHub 热点速览」