百度松果菁英班OJ【连载】

第十六周

2 的 n 次幂

• 高精度乘法

#include<bits/stdc++.h> 

using namespace std;

vector<int> mul(vector<int> &A) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * 2;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    int n;
    cin >> n;
    vector<int> A;
    A.push_back(1);
    while (n--) {
        A = mul(A);
    }
    for (int i = A.size() - 1; i >= 0; i--) {
        printf("%d", A[i]);
    }
    return 0;
}

个数统计

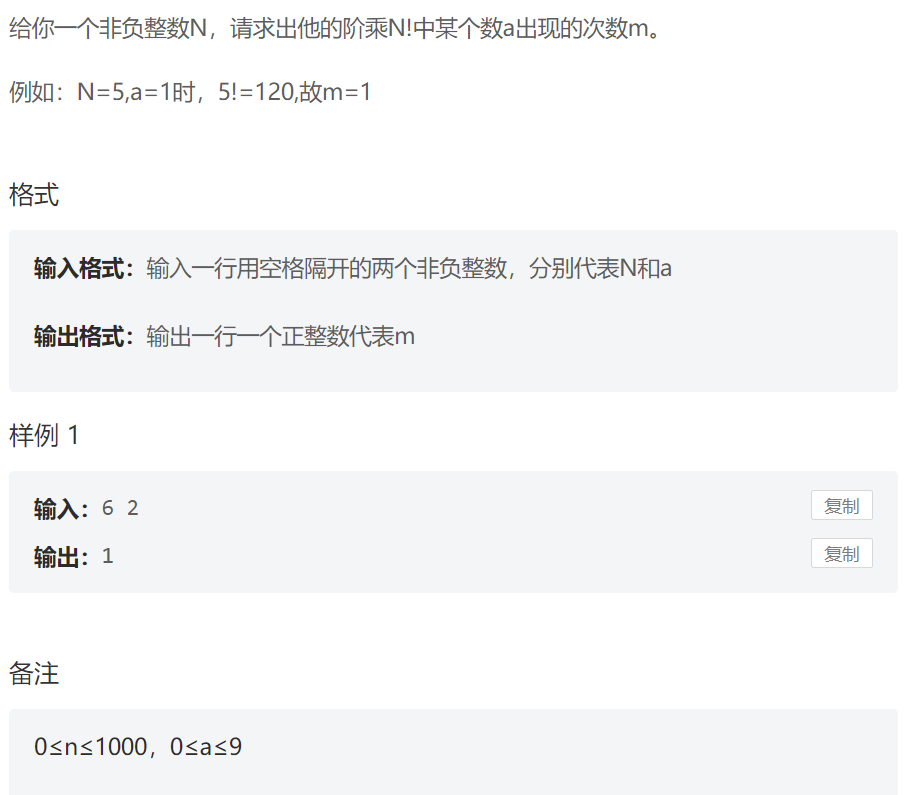
• 高精度乘法求阶乘
• 个数统计

#include<bits/stdc++.h> 

using namespace std;

vector<int> mul(vector<int> &A, int x) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * x;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main( )
{
    int N, a;
    cin >> N >> a;
    vector<int> A;
    A.push_back(1);
    for (int i = 2; i <= N; i++) {
        A = mul(A, i);
    }
    int ans = 0;
    for (int i = A.size() - 1; i >= 0; i--) {
        if (A[i] == a) ans++;
    }
    cout << ans << endl;
    return 0;
}

数组扞插

题目复述：

• 将数组分为三部分，前半段，后半段，和中间的数（如果数组大小是奇数）
• 前半段升序排列
• 后半段降序排列
• 如果有中间的数字，则中间的数不参与排列，直接放到结果数组的末尾

#include<bits/stdc++.h> 

using namespace std;

int n;
const int N = 10010;
int a[N], b[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int l = n + 1 >> 1; // 前半段 + 中间数字（可能没有）
    int r = n - l;      // 后半段
    if (l == r) {       // 前后一样多
        sort(a, a + l, less<int>());
        sort(a + l, a + n, greater<int>());
    }
    else {              // 前面多一个，则中间的数不参与排序
        sort(a, a + l - 1, less<int>());
        sort(a + l, a + n, greater<int>());
    }
    int ll = 0, rr = l;

    // 交叉插入结果数组
    for (int i = 0; i < n; i++) {
        if (i % 2 == 0) b[i] = a[ll++];
        else b[i] = a[rr++];
    }
    for (int k = 0; k < n; k++) {
        printf("%d ", b[k]);
    }
    return 0;
}

MXR 竞赛

题目复述：

• N 个问题，都有积分，范围为负数、零和正数
• 选出所有一个积分子集，使得子集中的所有积分的乘积得到最大值

解法：

• 贪心思想
• 所有积分从小到大排序，所有正数全部参与乘积
• 所有负数，相邻两个负数相乘得到正数。从左向右遍历，只要相邻两个积分是负数，则这两个负数都参与乘积；最后可能剩下一个绝对值最小的负数，不参与乘积
• 特殊情况：如果所有积分都没有选取，比如只有一个负数，返回数组最后一个数（最大）

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
long n;
int a[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    long ans = 1;       // 注意精度，int 会爆精度
    int flag = 0;
    sort(a, a + n);
    for (int i = 0; i < n; i++) {
        if (a[i] < 0) {
            if (i < n - 1 && a[i + 1] < 0) {
                ans = ans * (a[i] * a[i + 1]);
                ans %= 998244353;
                i++;
                flag++;
            }
        } else if (a[i] > 0) {
            ans = ans * a[i];
            ans %= 998244353;
            flag++;
        }
    }
    if (flag == 0) printf("%d", a[n - 1]);
    else printf("%d", ans);
    return 0;
}

小码哥的跳棋游戏

题目复述：

• 没有棋子不消耗能量
• 一次最多跳过一个棋子
• 破坏一个棋子消耗一个能量
• 求消耗最小能量从 0 位置到达 n 位置

解法：

• 贪心思想 + 双指针
• 对于连续 n 个棋子，n 为奇数，最少破坏 ⌊n / 2⌋ 个棋子
• 对于连续 n 个棋子，n 为偶数，最少破坏 n / 2 个棋子
• 由于 int 除法自动取整特性，以上两种情况可以合并

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
int a[N];

int main( )
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int ans = 0;
    int i = 0;
    while (i < n) {
        // 出现棋子
        if (a[i] == 1) {
            int count = 1;
            int j;
            // 统计连续棋子个数
            for (j = i + 1; j < n && a[j] == 1; j++) {
                 count++;
            }
            ans += count / 2;
            // 破坏之后就可以跳动了
            i = j;
        } else {
            // 没有棋子就直接跳
            i++;
        }
    }
    // 由于跳动到第 n 块，如果第 n - 1 块是棋子，需要破坏
    if (a[n - 1] == 1) ans++;
    cout << ans;
    return 0;
}

矩阵乘法

• 常规矩阵乘法

#include<bits/stdc++.h> 

using namespace std;

const int N = 1010;
int a[N][N], b[N][N], c[N][N];
int l, m, n;
void mul(int a[][N], int b[][N]) {
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < n; j++) {
            for (int k =0; k < m; k++) {
                c[i][j] += a[i][k] * b[k][j];
            }
        }
    }
}

int main( )
{
    cin >> l >> m >> n;
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < m; j++) {
            scanf("%d", &a[i][j]);
        }
    }
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &b[i][j]);
        }
    }
    mul(a, b);
    for (int i = 0; i < l; i++) {
        for (int j = 0; j < n; j++) {
            printf("%d ", c[i][j]);
        }
        printf("\n");
    }
    return 0;
}

第十七周

无重复字符的最长子串

解法：

• 滑动窗口
• 数组模拟哈希，或者使用哈希表
• 需要注意，字符串还可能包含空格，如果使用 cin 读取到空格就停止了，可以使用 getline 读取

#include<bits/stdc++.h> 

using namespace std;

int main( )
{
    string s;
    getline(cin, s);  // 读取一行字符串，需要使用 string 类型存储
    int ans = 0;
    int flag[128];    // 哈希表
    memset(flag, 0, sizeof flag);  // 初始化哈希表
    int j = 0;        // 窗口左端
    for (int i = 0; i < s.size(); i++) {  // 窗口右端
        flag[s[i]]++;
        while (flag[s[i]] > 1) {  // 只要哈希表中元素 s[i] 数量大于 1 就缩小窗口，右移窗口左端点
            flag[s[j]]--;
            j++;
        }
        ans = max(ans, i - j + 1); // 每次更新答案
    }
    cout << ans;
    return 0;
}

A + B problem

• 简单版本，高精度模板

#include<bits/stdc++.h> 

using namespace std;

vector<int> add(vector<int> A, vector<int> B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size() || t; i++) {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    return C;
}

int main( )
{
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) {
        A.push_back(a[i] - '0');
    }
    for (int i = b.size() - 1; i >= 0; i--) {
        B.push_back(b[i] - '0');
    }
    auto C = add(A, B);
    for (int i = C.size() - 1; i >= 0; i--) {
        printf("%d", C[i]);
    }
    return 0;
}

• 面向对象，运算符重载

#include <bits/stdc++.h>

using namespace std;

class Num {
public:
    Num(string s) {
        for (int i = s.size() - 1; i >= 0; i--) {
            A.push_back(s[i] - '0');
        }
    }
    Num(vector<int> &A) {
        this->A = A;
    }
    Num operator+(const Num &b) {
        vector<int> C;
        vector<int> A = this->getVector();
        vector<int> B = b.getVector();
        int t = 0;
        for (int i = 0; i < A.size() || i < B.size() || t; i++) {
            if (i < A.size())
                t += A[i];
            if (i < B.size())
                t += B[i];
            C.push_back(t % 10);
            t /= 10;
        }
        Num c(C);
        return c;
    }
    vector<int> getVector() const {
        return A;
    }
    void print() {
        for (int i = A.size() - 1; i >= 0; i--) {
            printf("%d", A[i]);
        }
    }

private:
    vector<int> A;
};

int main() {
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    Num numA(a);
    Num numB(b);
    Num numC = numA + numB;
    numC.print();
    return 0;
}

调整队伍

题目复述：

• 给出的数组表示排队情况，数组中的元素代表学生编号，数组下标表示学生排队顺序，从 1 到 n
• 教官给出 x y 0 表示学生 x 放到 y 之前
• 教官给出 x y 1 表示学生 x 放到 y 之后

解法：

• 一般的想法是进行模拟，每次都改变数组元素位置，时间复杂度 O(m*n)，应该是过不了
• 因为涉及到元素交换，且元素之间有顺序，自然想到使用链表，但是一般链表只能表示元素之间的前后相对关系，无法以进行索引查找，没法一下定位到某个同学
• 进而想到使用静态链表，也就是数组模拟链表，因为涉及到获取前后元素的操作，要使用双向链表

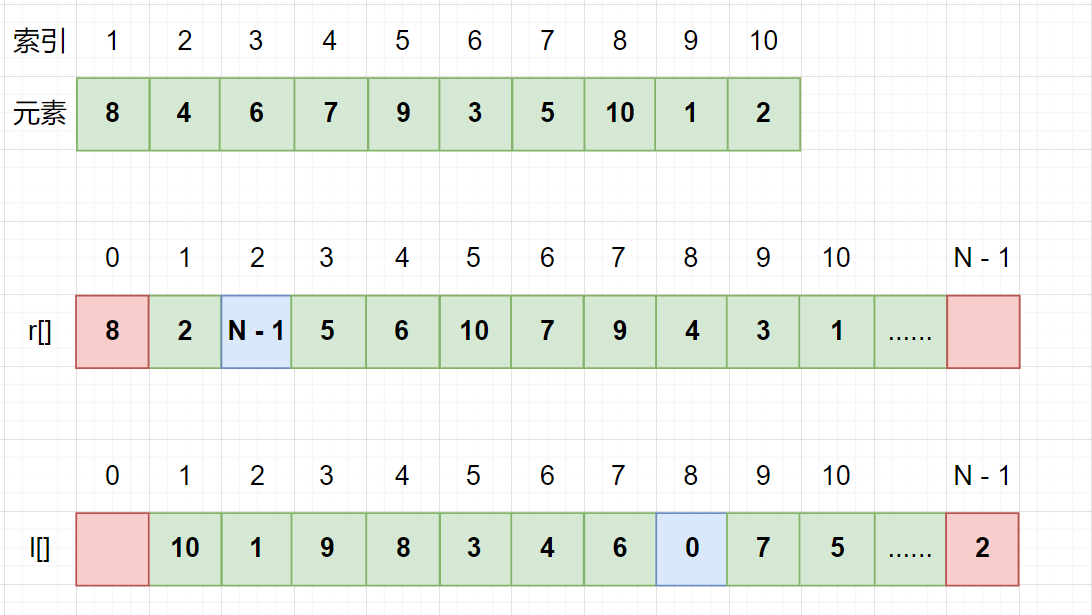
• r 数组记录当前元素右边的元素是什么，比如 r[8] = 4 表示 8 号学生右侧是 4 号学生
• l 数组记录当前元素左边的元素是什么，比如 r[2] = 1 表示 2 号学生左侧是 1 号学生
• 注意，头和尾都使用了哨兵节点，节点 0 和节点 N - 1 为哨兵节点

#include<bits/stdc++.h> 

using namespace std;

const int N = 300010;
int a[N], r[N], l[N];

// 初始化哨兵节点
void init() {
    r[0] = N - 1;
    l[N - 1] = 0;
}

// 将 x 插入 y 之前
void putFront(int x, int y) {
    // 删除 x
    l[r[x]] = l[x];
    r[l[x]] = r[x];
    // 插入到 y 之前
    r[x] = y;
    l[x] = l[y];
    r[l[y]] = x;
    l[y] = x;
}

// 将 x 插入 y 之后
void putRear(int x, int y) {
    // 删除 x
    l[r[x]] = l[x];
    r[l[x]] = r[x];
    // 插入到 y 之后
    l[x] = y;
    r[x] = r[y];
    l[r[y]] = x;
    r[y] = x;
}

int main( )
{
    int n, m;
    cin >> n >> m;
    init();
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    // 初始化 r 数组
    int idx = 0;     // idx 表示当前要处理的节点，初始从前往后处理
    for (int i = 0; i < n; i++) {
        r[idx] = a[i];
        idx = a[i];
    }
    r[idx] = N - 1;  // 注意维持尾哨兵和最后一个元素的关系
    idx = N - 1;     // 从后往前处理
    for (int i = n - 1; i >= 0; i--) {
        l[idx] = a[i];
        idx = a[i];
    }
    l[idx] = 0;      // 注意维持头哨兵和第一个元素的关系
    while (m--) {
        int x, y, op;
        scanf("%d%d%d", &x, &y, &op);
        if (op == 0) {
            putFront(x, y);
        } else {
            putRear(x, y);
        }
    }
    for (int i = r[0]; i != N - 1; i = r[i]) {
        printf("%d ", i);
    }
    return 0;
}

配对打深渊

解法：

• 原题型是运动员最佳配对问题，该题只是改了改描述
• 需要考虑到所有组合，类似全排列，使用回溯法解决
• 限界条件：当前已配对火水伤害总和 + 未配对火水可能的最大伤害 < 已求出的总配对伤害，剪枝

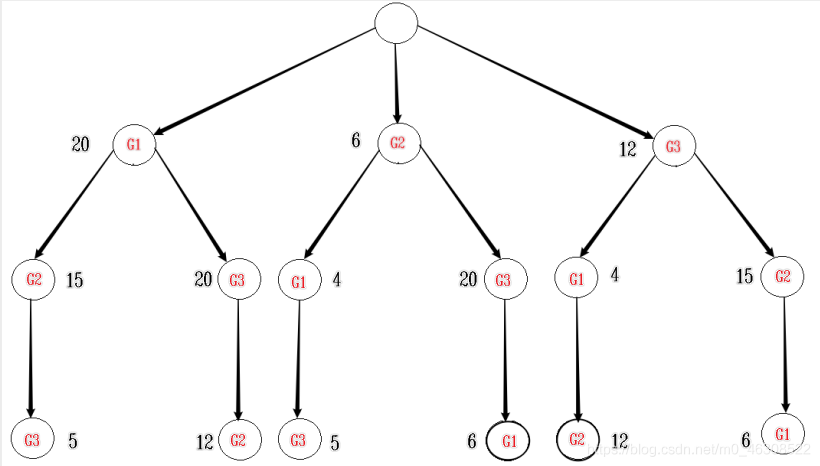
• 本题采用的是火系选水系的方法，这样就构成了一棵排列树。
• G表示水系，排列树的层数表示火系。
• 如第一层的 G1 = 20 表示，火系 1 号选水系 1 号的水火双方配对伤害为 20。
• 如第二次的 G3 = 20 表示，火系 2 号选水系 3 号的水火双方配对伤害为 20。

#include<bits/stdc++.h> 

using namespace std;

const int N = 21;

// P，Q 记录数据；data[i][j] 表示火系 i 和水系 j 的配对伤害；fireMax[i] 表示 火系 i 与所有的水系配对的最大伤害；book 记录哪个水系访问过了
int P[N][N], Q[N][N], data[N][N], fireMax[N], book[N];

// n 表示矩阵维数；Max 表示各组配对伤害总和最大值；sum 表示当前配对伤害之和
int n, Max, sum;

// 回溯
void dfs(int level) {
    // 递归出口
    if (level >= n) {         // 已经访问到第 n 个火系（从 1 开始）
        Max = max(Max, sum);  // 更新 Max
        return;
    }
    // 剪枝
    int afterSum = 0;         
    for (int i = level; i < n; i++) {  // 求得火系从第 level 个到第 n - 1 个的最大配对伤害之和
        afterSum += fireMax[i];
    }
    if (sum + afterSum < Max) return;  // 剪枝

    // 遍历所有水系，如果该水系还未被访问，则访问该水系，更新 sum，递归到下一层
    for (int i = 0; i < n; i++) {
        if (!book[i]) {
            book[i] = 1;
            sum += data[level][i];
            dfs(level + 1);
            sum -= data[level][i];
            book[i] = 0;
        }
    }
}

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &P[i][j]);
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &Q[i][j]);
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            data[i][j] = P[i][j] * Q[j][i];    // 记录火系 i 和水系 j 的配对伤害
            fireMax[i] = max(fireMax[i], data[i][j]); // 获取火系 i 的所有配对中的最大伤害
        }
    }
    dfs(0);
    cout << Max;
    return 0;
}

第十八周

匹配图

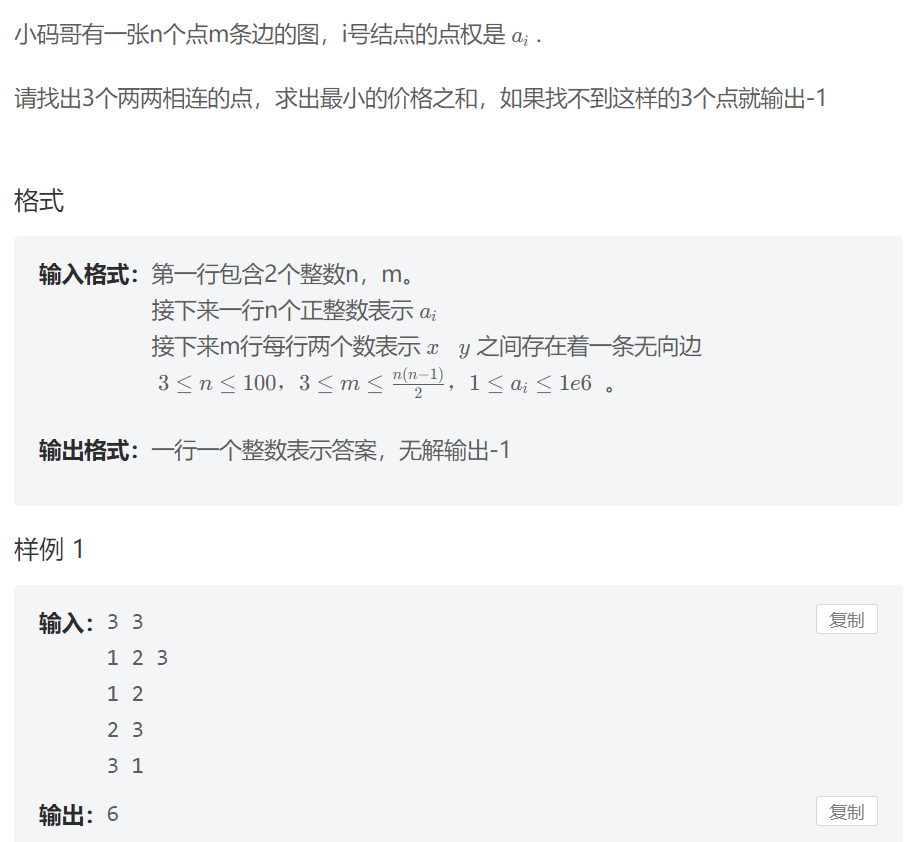
• n 很小，直接邻接矩阵枚举即可

#include<bits/stdc++.h> 

using namespace std;

const int N = 110;
int g[N][N], val[N];
int n, m;

int main( )
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &val[i]);
    }
    int a, b;
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &a, &b);
        g[a][b] = 1;
        g[b][a] = 1;
    }
    int ans = INT_MAX;
    for (int i = 1; i <= n; i++) {
        for (int j = i + 1; j <= n; j++) {
            for (int k = j + 1; k <= n; k++) {
                if (g[i][j] == 1 && g[j][k] == 1 && g[k][i] == 1) {
                    ans = min(ans, val[i] + val[j] + val[k]);
                }
            }
        }
    }
    cout << ans;
    return 0;
}

字符串构造

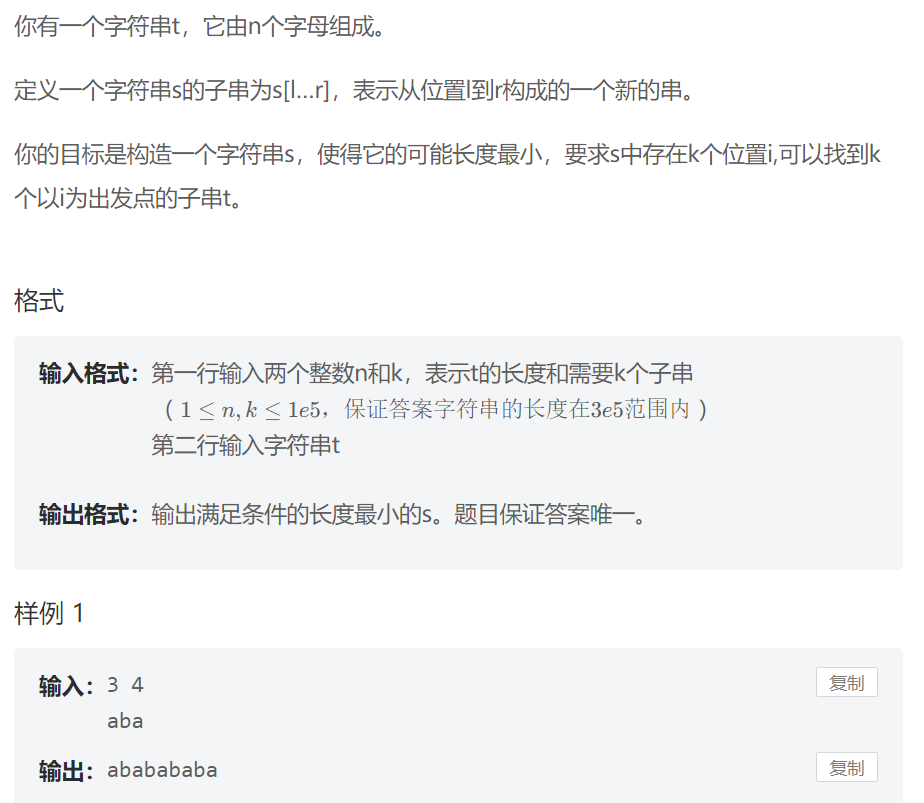
解法：

• kmp 最小循环节

结论：假设 S 的长度为 len，则 S 存在最小循环节，循环节的长度 L 为 len - next[len]，子串为 S[0 … len - next[len] - 1]。

1. 如果 len 可以被 len - next[len] 整除，则表明字符串 S 可以完全由循环节循环组成，循环周期 T = len / L。
2. 如果不能，说明还需要再添加几个字母才能补全。需要补的个数是循环个数 L - len % L = L - (len - L) % L = L - next[len] % L，L = len - next[len]。

• 本题利用 next[n] 得知最长相等前后缀长度，从 k = 2 开始构造时每次只需要补上 原字符串 - 最大前缀 即可。

• 例如 abcab ，最长相等前后缀是 ab，原字符串 - 最大前缀 = cab，从第二次开始，每次补上 cab，可以与前面字符串的后缀 ab 构成一个子串

#include<bits/stdc++.h> 

using namespace std;
const int N = 3e5 + 10;
char p[N];
int n, k, ne[N];

int main( )
{
    cin >> n >> k >> p + 1;

    // 构造 next 数组
    for (int i = 2, j = 0; i <= n; i++) {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j++;
        ne[i] = j;
    }
    string s;
    int cnt = 0, j = 0;
    while (cnt < k) {
        s += p[j + 1];
        j++;
        if (j == n) {
            j = ne[j];
            cnt++;
        }
    }
    cout << s << endl;
    return 0;
}

五彩斑斓的世界

• 递归

#include <iostream>
using namespace std;

// 处理从下标 i 开始的字符串
// 注意 i 使用引用类型，这样所有递归操作中共享变量 i，不会重复访问
int one_process(char* string, int &i) {
    int length = 0;
    while (string[i] != '\0') {
        int temp;
        switch(string[i++]) {
            case '(': {
                length += one_process(string, i);
                break;
            }
            case '|': {
                temp = one_process(string, i);
                return temp > length ? temp : length;
                break;
            }
            case ')': {
                return length;
                break;
            }
            default: {
                length++;
                break;
            }
        }
    }
    return length;
}
int main() {
    char string[100000] = {'\0'};
    int i = 0;
    scanf("%s", string);
    printf("%d", one_process(string, i));
    return 0;
}

• 利用栈

#include <iostream>
#include <stack>

using namespace std;

int main() {
    string s;
    cin >> s;
    stack<int> stk;
    stk.push(0);                   // 每一个 push0 作为新序列的开始
    for (int i = 0; s[i]; i++) {
        if (s[i] == 'a') {         // 如果是 a，则栈顶元素加一
            stk.top()++;
        } else if (s[i] == '|') {  // 如果是 |，则开始一个新序列
            stk.push(0);
        } else if (s[i] == '(') {  // 如果是 (，则入栈 -2，同时入栈 0，开始一个新序列
            stk.push(-2);
            stk.push(0);
        } else {                   // 如果是 )，则开始弹出直到遇到 (，统计最大值
            int num = 0;
            while (stk.top() != -2) {
                num = max(num, stk.top());
                stk.pop();
            }
            stk.pop();             // 弹出 (
            stk.top() += num;      // 弹出之后进行拼接
        }
    }
    int num = 0;
    while (!stk.empty()) {
        num = max(num, stk.top());
        stk.pop();
    }
    printf("%d", num);
}

随机排序

• 自定义结构体排序

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
int n, m;

struct student{
    int id, score;
    bool operator< (const student& stu) const {
        if (score != stu.score) return score > stu.score;
        else return id < stu.id;
    }
}students[N], t[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &students[i].id, &students[i].score);
    }
    cin >> m;
    while (m--) {
        int idx = 0;
        int p;
        while (cin >> p && p) {
            t[idx++] = students[p];
        }
        sort(t, t + idx);
        for (int i = 0; i < idx; i++) {
            printf("%d ", t[i].id);
        } 
        puts("");
    }
}

虚实流动

• 常规逆序对
• 利用题目性质，每个数字均出现一次，那么当 a 被移到末尾之后，逆序对就减少了 a 个(因为有 a 个数比 a 小，所以当 a 换到末尾后，在 a 前面且比 a 小的数就有 a 个，故逆序对就少了 a 个)，同理逆序对就增加了 n - a - 1 个，故将 a 转移到末尾后，就增加了 n - 2 * a - 1 个逆序对。

#include <iostream>

using namespace std;

const int N = 300010;
int a[N], tmp[N], n, backup[N];

int merge_sort(int a[], int l, int r) {
    if (l >= r) return 0;
    int mid = l + r >> 1;
    int sum = merge_sort(a, l, mid) + merge_sort(a, mid + 1, r);
    int i = l, j = mid + 1, k = 0; 
    while (i <= mid && j <= r) {
        if (a[i] <= a[j]) {
            tmp[k++] = a[i++];
        } else {
            tmp[k++] = a[j++];
            sum += mid - i + 1;
        }
    }
    for (i = l, j = 0; i <= r; i++, j++) {
        a[i] = tmp[j++];
    }
    return sum;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
        backup[i] = a[i];
    }
    int sum = merge_sort(a, 0, n - 1);
    printf("%d\n", sum);
    for (int i = 0; i < n - 1; i++) {
        sum += n - 2 * backup[i] - 1;
        printf("%d\n", sum);
    }
}

第二十周

上周太忙了，没抽出时间整理，等有空的时候再整理一下题目吧

数字统计

• 简单模拟

#include<bits/stdc++.h> 

using namespace std;

int getRev(int n) {
    int res = 0;
    while (n) {
        int t = n % 10;
        res = res * 10 + t;
        n /= 10; 
    }
    return res;
}

int main( )
{
    int n; 
    cin >> n;
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        int t = getRev(i);
        if (i % t == 0) ans++;
    }
    cout << ans;
    return 0;
}

项链

题目复述：

• n 个数循环排列，找到相邻点之差的绝对值总和最大

解法：

• 贪心
• 先从小到大排序
• 考虑第一种极端情况，最小数 a[0] 和 a[n - 1] 构成最大差值
• 考虑第二种情况，a[n - 1] 和 a[1] 的差值第二大
• 考虑第三种情况，a[1] 和 a[n - 2] 的差值第三大
• 以此类推，找到规律，左右两个指针向中间遍历，间隔放置元素，构成最大序列

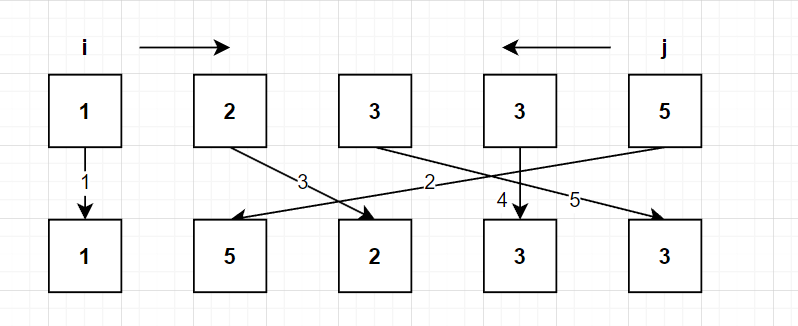
#include<bits/stdc++.h> 

using namespace std;

const int N = 300010;
int n, a[N], b[N];

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    sort(a, a + n);
    int i = 0, j = n - 1, k = 0;
    while (i <= j) {
        if (i <= j) {
            b[k++] = a[i++];
        }
        if (i <= j) {
            b[k++] = a[j--];
        }
    }
    int ans = 0;
    for (int i = 0; i < n - 1; i++) {
        ans += abs(b[i + 1] - b[i]);
    }
    ans += abs(b[n - 1] - b[0]);
    cout << ans;
    return 0;
}

圈竹鼠

• 计算几何凸包模板题

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
 
using namespace std;
 
const double epsi = 1e-8;
const double pi = acos(-1.0);
const int maxn = 100010;
 
 
struct PPoint{   
	double x;
	double y;
 
	PPoint(double _x = 0, double _y = 0): x(_x), y(_y) {
	}
 
	PPoint operator - (const PPoint& op2) const {
		return PPoint(x - op2.x, y - op2.y);
	}
 
	double operator^(const PPoint &op2) const {
		return x * op2.y - y * op2.x;
	}
};
 
 
inline int sign(const double &x) {
	if(x > epsi){
		return 1;
	}
	if(x < -epsi){
		return -1;
	}
	return 0;
}
 
inline double sqr(const double &x) {
	return  x*x;
}
 
inline double mul(const PPoint& p0, const PPoint& p1, const PPoint& p2) {
	return (p1 - p0)^(p2 - p0);
}
 
inline double dis2(const PPoint &p0, const PPoint &p1){
	return sqr(p0.x - p1.x) + sqr(p0.y - p1.y);
}
 
inline double dis(const PPoint& p0, const PPoint& p1){
	return sqrt(dis2(p0,p1));
}
 
int n;
double l;
PPoint p[maxn];
PPoint convex_hull_p0;
 
 
inline bool convex_hull_cmp(const PPoint& a, const PPoint& b) {
	return sign(mul(convex_hull_p0,a,b) > 0) || sign(mul(convex_hull_p0, a, b)) == 0 && dis2(convex_hull_p0, a) < dis2(convex_hull_p0, b);
}
 
 
/**
 * 计算点集a[]的凸包b[]。其中点集a有n个元素
 */
int convex_hull(PPoint* a,int n, PPoint* b) {
	if(n < 3) {   //如果顶点数小于3,构不成一个凸包
		return -1;
	}
	int i;
	for(i = 1; i < n ; ++i) {//遍历点集中的每一个点
		//寻找最低点(所谓的最低点就是最靠左下角的点)
		if(sign(a[i].x - a[0].x) < 0 || (sign(a[i].x - a[0].x) == 0 && sign(a[i].y < a[0].y) < 0 )) {
			swap(a[i], a[0]);
		}
	}
 
	convex_hull_p0 = a[0];
	sort(a, a+n, convex_hull_cmp);//排序
 
	int newn = 2;
	b[0] = a[0];
	b[1] = a[1];
 
	/**
	 * 在剩下的点中不断前进,如果当前点在前进方向左侧,
	 * 则将当前点进栈,否则将最近入栈的点出栈.知道当前点在前进方向的左侧
	 */
	for(i = 2; i < n ; ++i){
		while(newn > 1 && sign(mul(b[newn-1], b[newn-2], a[i])) >= 0) {
			newn--;
		}
 
		b[newn++] = a[i];//江当前点进栈
	}
 
	return newn;//返回栈顶指针
}
 
int main(){
	 cin >> n;
	int i;
	for(i = 0; i < n ; ++i){
		scanf("%lf%lf", &p[i].x, &p[i].y);
	}

	n = convex_hull(p, n, p);
	p[n] = p[0];

	double ans = 0;
	for(i = 0; i < n ; ++i) {//求凸包的周长
		ans += dis(p[i], p[i+1]);
	}
	printf("%.2lf\n", ans);
	return 0;
}

σ 函数

• 数论：唯一分解定理 + 约数和

#include<bits/stdc++.h> 

using namespace std;

typedef long long LL;

int main() {
    LL n;
    scanf("%lld",&n);
    LL ans = n - (LL)sqrt(n) - (LL)sqrt(n/2);
    printf("%lld\n" ,ans);
}

第二十一周

我得重新集结部队

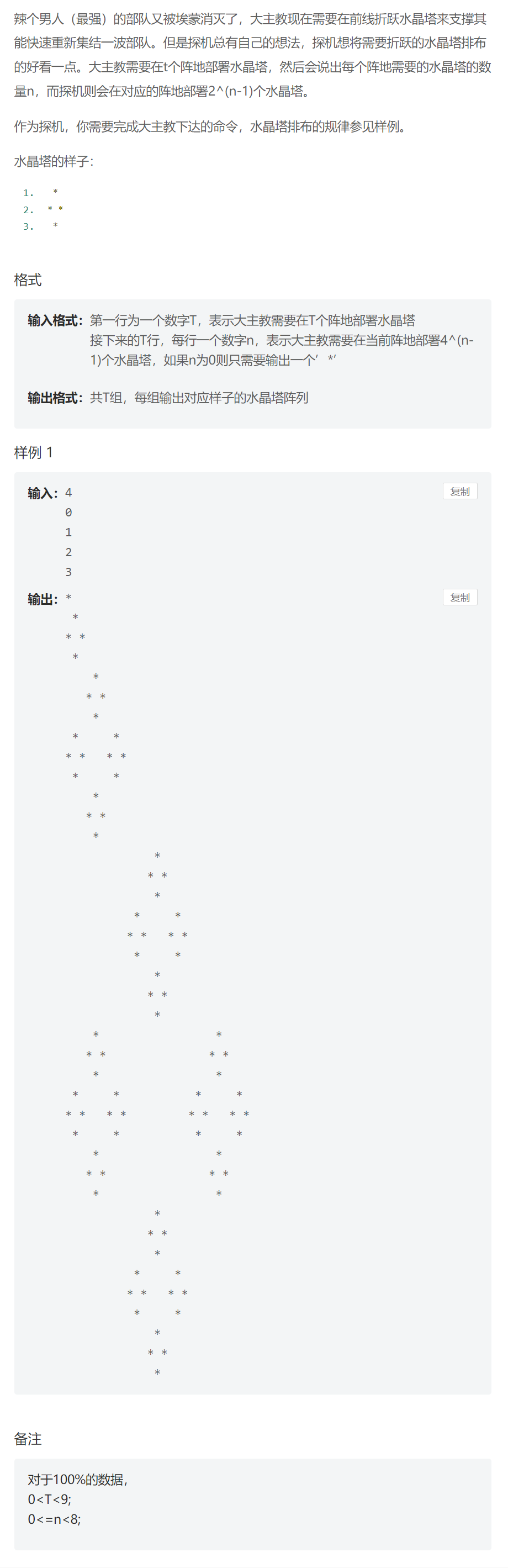
• 递归画图
• 找中心和倍数

#include<bits/stdc++.h> 

using namespace std;

const int MAX = 5000;
char grid[MAX][MAX] = {};

int Pow(int n)
{
    int p = 1;
    for (int i = 1; i <= n; ++i) {
        p *= 3;
    }
    return p;
}

void draw(int n, int x, int y)
{
    if (n == 0) {
        grid[x][y] = '*';
    } else {
        int size = Pow(n-1);
        draw(n-1, x, y - size);
        draw(n-1, x - size, y);
        draw(n-1, x + size, y);
        draw(n-1, x, y + size);
    }
}

void print(int size)
{
    int end[MAX];
    for (int i = 0; i < size; ++i) {
        for (int j = 0; j < size; ++j) {
            if (grid[i][j] != ' ') end[i] = j;
        }
    }
    for (int i = 0; i < size; ++i) {
        for (int j = 0; j <= end[i]; ++j) {
            cout << grid[i][j];
        }
        cout << endl;
    }
}

void loop(int n)
{
    memset(grid, ' ', sizeof(grid));
    int size = Pow(n);
    draw(n, size/2, size/2);
    print(size);
}

int main()
{
    int t, n;
    cin >> t;
    while (t--) {
        cin >> n;
        loop(n);
    }
}

逐夜烁光

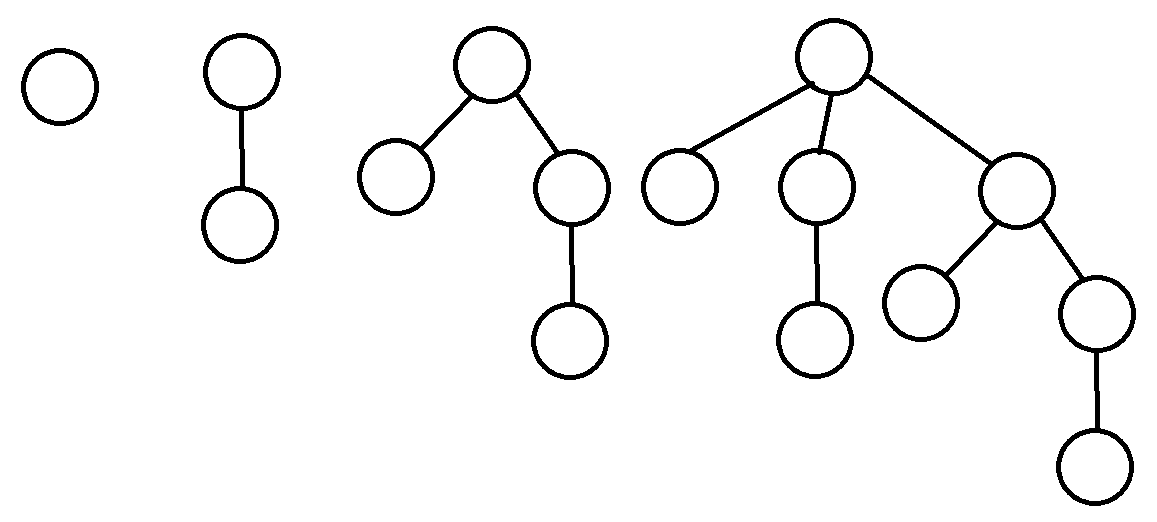
• 玄学：注意到 k = 0 时，n = 1；k = 1 时，n = 2；k = 2 时，n = 4；k = 3 时，n = 8
• 猜测：当 n 为 2 的幂时，答案成立
• 验证：成功

#include<bits/stdc++.h> 

using namespace std;

int n;
// 1 2 4 8
int main( )
{
    cin >> n;
    int sum = 0;
    while (n != 0) {
        sum += (n & 1);
        n >>= 1;
    }
    if (sum == 1) puts("YES");
    else puts("NO"); 
    return 0;
}

数组稳定度

#include<bits/stdc++.h> 

using namespace std;

const int N = 100010;
int a[N], n;

int main( )
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    sort(a, a + n);
    int one = a[n - 1] - a[1];
    int two = a[n - 2] - a[0];
    cout << (one < two ? one : two);
    return 0;
}

• 简单模拟，要么删最大，要么删最小

水往低处流

题目复述

• 格子浇水，高的格子可以灌溉低的格子
• 问最少浇多少次能把整块地浇完

解法

• 染色法：浇过水的格子设为 0
• 优先队列 + bfs：所有格子按照高度从大到小排列，优先从高的格子开始浇水，最大程度染色

#include<bits/stdc++.h> 

using namespace std;

const int N = 2010;
int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};  // 方向数组
int g[N][N], n;

typedef struct grid {    // 格子结构体
    int x, y, h;
    bool operator < (const grid g) const {  // 重载操作符实现优先队列从大到小排序
        return h < g.h;
    }
} G;

void bfs(int x, int y) {
    int h = g[x][y]; 
    g[x][y] = 0; // 染色
    for (int i = 0; i < 4; i++) {  // bfs 遍历
        int xx = x + dx[i];
        int yy = y + dy[i];

        // 如果在边界内并且未被染色则递归 bfs
        if (xx >= 0 && xx < n && yy >= 0 && yy < n && g[xx][yy] > 0 && g[xx][yy] < h) { 
            bfs(xx, yy);
        }
    }
}

int main( )
{
    cin >> n;
    priority_queue<G, vector<G>, less<G>> heap;  // 优先队列
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &g[i][j]);
            G point = {i, j, g[i][j]};
            heap.push(point);
        }
    }
    int ans = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            G point = heap.top();
            heap.pop();
            if (g[point.x][point.y] > 0) {
                bfs(point.x, point.y);
                ans++;
            }
        }
    }
    cout << ans << endl;
    return 0;
}