算法设计与分析「通关指南」
绪论与算法基础
算法的基本内容(算法设计的基本步骤)
- 算法设计
- 算法表示
- 算法确认
- 算法分析
- 程序测试
算法的重要特性:
- 确定性:每一种运算必须要有确切的定义,无二义性;
- 能行性:运算都是基本运算,原则上能在有限时间内完成;
- 输入:有0个或多个输入;
- 输出:一个或多个输出;
- 有穷性:在执行了有穷步运算后终止
算法分析的两个步骤:
- 事前分析
- 分析算法中基本运算的执行次数
- 分析算法的执行时间的渐进表示
- 事后测试
- 作时空性能分布图
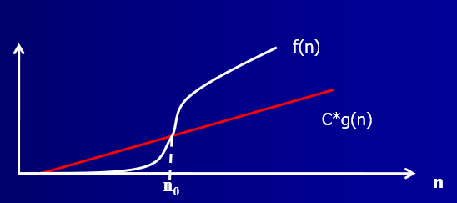
1️⃣ 定义:如果存在两个正常数 和 ,对于所有的 ,有 ,则记作

🐍 例题:判断
☁️ 分析:是否存在 和 ,对于所有的 ,满足 , 考虑 可知,只需
☀️ 证明: ,均有
🌋 证明题:





-
多项式时间算法(polynomial time algorithm):

-
指数时间算法(exponential time algorithm):
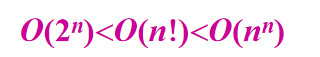
2️⃣ 定义:如果存在两个正常数 和 ,对于所有的 ,有 ,则记作
🌋 证明题:




3️⃣ 定义:如果存在两个正常数 c1, c2 和n0,对于所有的n n0,有 c1|g(n)| |f(n)| c2|g(n)|,则记作:f(n)=(g(n)) .
🔔 渐近表示函数的若干性质
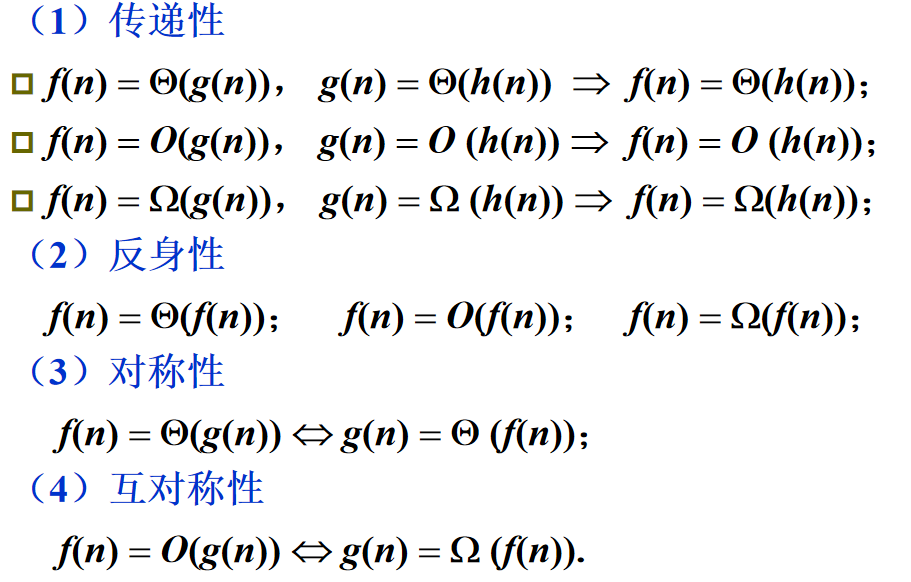

☀️ 作业题


分治法
什么是分治法

- 分解(Divide):将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小。
- 解决(Conquer):递归地求解出子问题。如果子问题的规模足够小,则停止递归,直接求解。
- 合并(Combine):将子问题的解合成原问题的解。
🍎 适用条件
- 问题规模越小越易解决(有出口)
- 问题具有最优子结构(问题规模可分解)
- 分解出的各子问题的解可以合并为该问题的解
- 各子问题相互独立
分治策略 DANDC 的抽象化控制
procedure DANDC(p, q)
global n, A(1:n);
integer m, p, q;
if SMALL(p, q) // 判断输入规模 q-p+1 是否足够小,可直接求解
then return (G(p, q)) // G 是求解该规模问题的函数
else m <- DIVIDE(p, q) // 分割函数,p<=m<=q 原问题被分解为 A(p:m) 和 A(m+1:q) 两个子问题
return (COMBINE(DANDC(p, m), DANDC(m + 1, q))) // 合并函数,将两个子问题的解合并为原问题的解
end if
end DANCE
二分策略 DANCE 的计算时间
假设所分成的两个子问题的输入规模大致相等,则分治策略 DANDC 的计算时间可表示为:
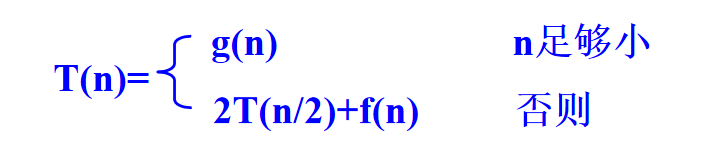
-
T(n) 是输入规模为 n 的分治策略的计算时间
-
g(n) 是对足够小的输入规模能直接计算出答案的时间
-
f(n) 是问题分解及 COMBINE 函数合成原问题解的计算时间
对以下两种情况求解递归关系式:
1️⃣ g(n) = O(1) 和 f(n) = O(n)
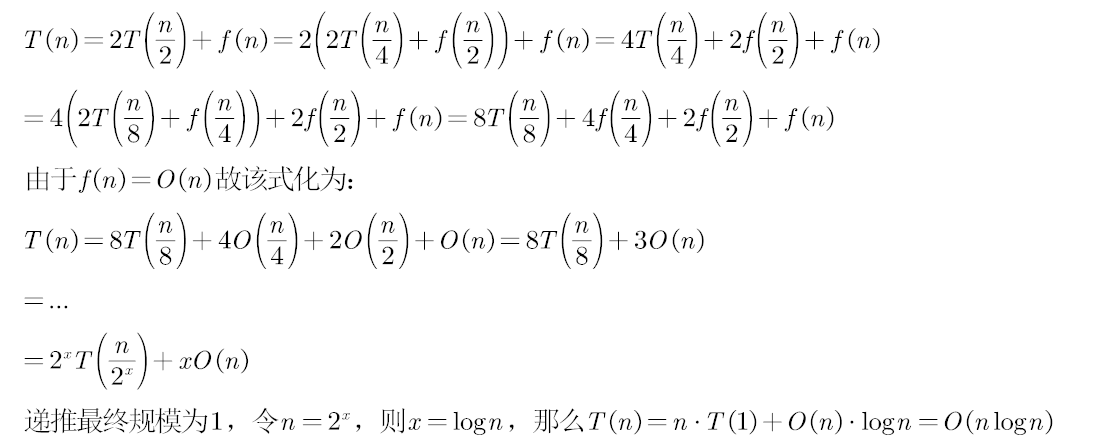
2️⃣ g(n) = O(1) 和 f(n) = O(1)

主定理

a:归约后的子问题个数n/b:规约后子问题的规模O(n^d):归约过程及组合子问题的解的工作量(多项式)
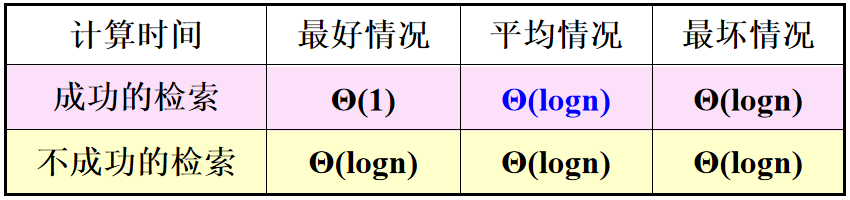
二分检索
procedure BINSRCH(A, n, x, j)
interger low, high, mid, j, n;
low <- 1; high <- n;
while low <= high do
mid <- (low + high) / 2 // 取中值
case
:x < A(mid): high <- mid - 1 // 寻找前一半
:x > A(mid): low <- mid + 1 // 寻找后一半
:else: j <- mid; return; // 检索成功,结束
endcase
repeat
j <- 0 // 检索失败
end BINSRCH
【数据结构与算法】简单排序(选择、冒泡、插入、希尔排序)、二分查找
时间复杂度分析:
T (n) = T (n/2) + O (1)
利用主公式,a = 1,b = 2,d = 0,故有 log(b, a) = d = 0,时间复杂度为 logn
🔔 以比较为基础检索的时间下界
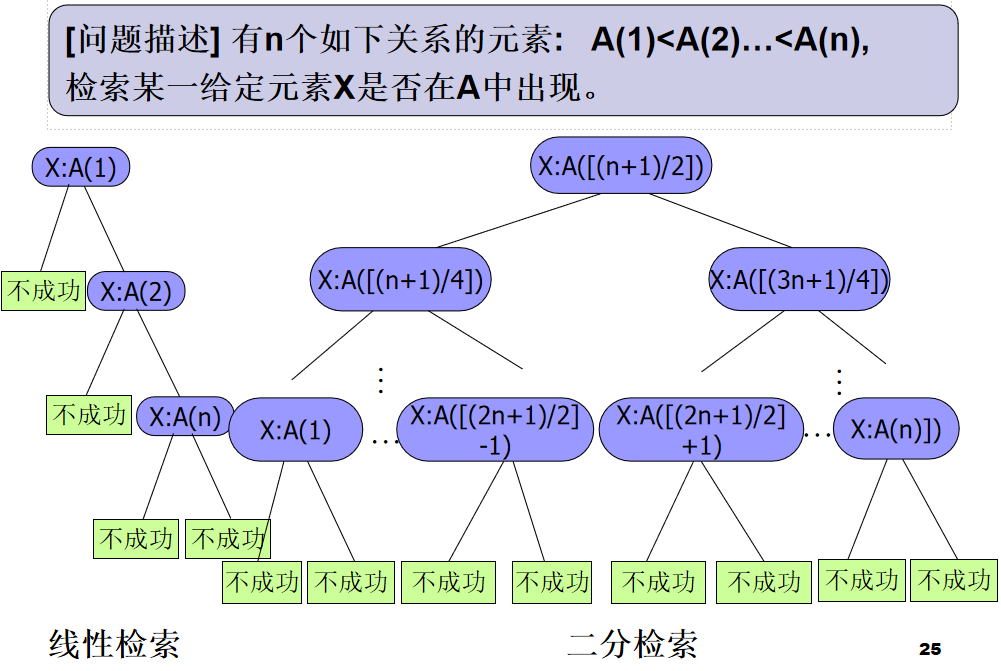
定理: 设A(1:n) 含有 n(n≥1) 个不同元素,排序为 A(1)<A(2)<…<A(n);又设以比较为基础去判断是否 x∈A(1:n) 的任何算法在最坏情况下所需的最小比较次数是 FIND(n),那么 FIND(n) ≥
定理:任何一种以比较为基础的算法,其最坏情况下的计算时间都不可能低于 O(logn),也就是不可能存在其最坏情况下计算时间比二分检索算法的计算时间数量级还低的算法。
结论:二分检索是解决检索问题的最优的最坏情况算法。
分治法求最大和最小元素
procedure MAXMIN(i, j, fmax, fmin)
int i, j; global n, A(1:n);
case
i= j: fmax ← fmin ← A[i]
i= j-1: if A[i]<A[j] then { fmax ← A[j]; fmin ← A[i]; }
else { fmax ← A[i]; fmin ← A[j]; }
else: {
mid=(i+j)/2;
call MAXMIN( i, mid, gmax, gmin)
call MAXMIN(mid+1, j, hmax, hmin)
fmax ← max(gmax, hmax);
fmin ← min(gmin, hmin);
}
endcase
end MAXMIN

三分检索
写一个“三分”检索算法,它首先检查 n/3 处的元素是否等于某个 x 的值,然后检查 2n/3 处的元素。这样,或者找到 x,或者把集合缩小到原来的 1/3。分析算法在各种情况下的计算复杂度。
procedure TriSearch(A, x, n, j)
integer low, high, p1, p2
low <- 1; high <- n;
while low <= high do
p1 <- (2low + high) / 3;
p2 <- (low + 2high) / 3;
case
:x = A(p1): j <- p1; return;
:x = A(p2): j <- p2; return;
:x < A(p1): high <- p1 - 1;
:x > A(p2): low <- p2 + 1;
:else: low <- p1 + 1; high <- p2 - 1;
endcase
repeat
j <- 0
end TriSearch
时间复杂度分析:
T(n) = T(n/3) + O(1)
利用主公式,a = 1,b = 3,d = 0,故有 log(b, a) = d = 0,时间复杂度为 logn

归并排序
-
分:将A(1),…A(n)平均分为 2 个子集合:A(1),…,A(n/2)和A(n/2 +1),…,A(n)
-
治:通过递归调用,对 2 个子集合分别分类
-
合:将 2 个已分类的子集合,合并为一个
procedure MERGESORT(low, high)
integer low, high, mid;
if low < high
mid = (low + high) / 2
call MERGESORT(low, mid)
call MERGESORT(mid + 1, high)
call MERGE(low, mid, high)
end MERGESORT
procedure MERGE(low, mid, high)
integer h, j, k, low, mid, high
global A(low: high); local B(low: high);
h <- low; i <- low; j <- mid + 1;
// 处理两个已经分类的序列
while h <= mid and j <= high do
if A(h) <= A(j) then B(i) <- A(h); h <- h + 1;
else B(i) <- A(j); j <- j + 1;
i <- i + 1
// 剩余元素处理
if h > mid then for k <- j to high do
B(i) <- A(k); i <- i + 1;
else for k <- h to mid do
B(i) <- A(k); i <- i + 1
// 将已分类的集合复制到A数组
for k <- low to high do A(k) <- B(k);
end MERGE
时间复杂度分析
T(n) = 2T(n/2) + O(n)
利用主公式,a = 2,b = 2,d = 1,故有 log(b, a) = d = 1,时间复杂度为 nlogn
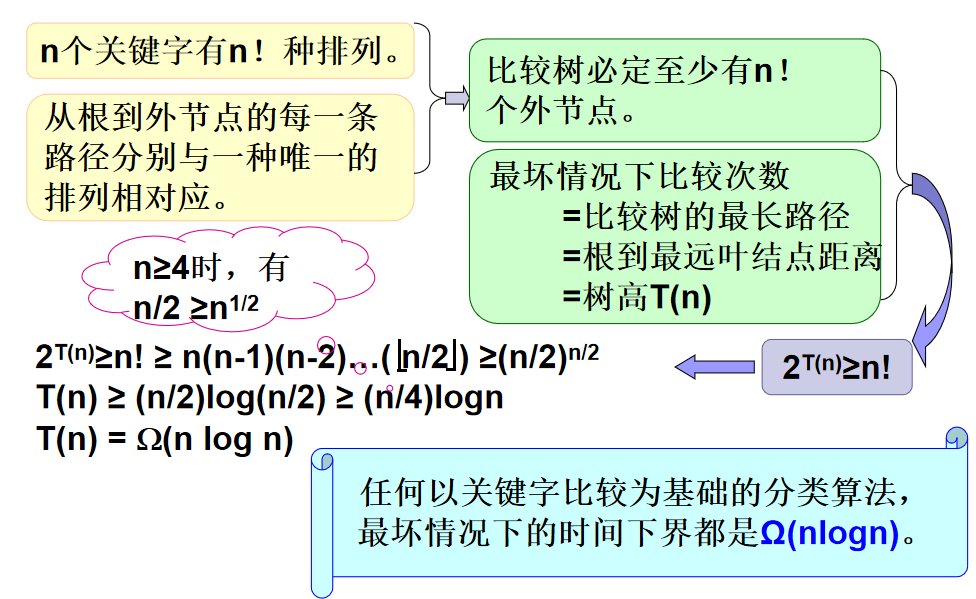
🔔 以比较为基础分类的时间下界
定理:任何以关键字比较为基础的分类算法,最坏情况下的时间下界都是 Ω(nlogn)
斯特拉森矩阵乘法
传统矩阵乘法:
public int[][] matrixMultiply(int[][] a, int[][] b) {
int rowa = a.length;
int colb = b[0].length;
int common = b.length;
int[][] ans = new int[rowa][colb]
for(int i = 0; i < rowa; i++) {
for(int j = 0; j < colb; j++) {
for(int k = 0; k < common; k++) {
ans[i][j] += a[i][k] * b[k][j];
}
}
}
return ans;
}
A 和 B 的乘积矩阵 C 中的元素 C[i][j]定义为:
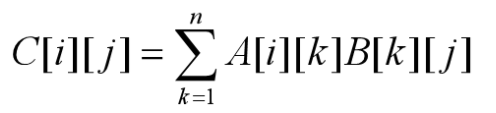
若依此定义来计算 A 和 B 的乘积矩阵 C,则每计算 C 的一个元素 C[i][j],需要做 n 次乘法和 n-1 次加法。因此,算出矩阵 C 的个元素所需的计算时间为 Θ(n^3)。
斯塔拉森算法的实现基础:
分治策略:假定 A 和 B 的级数 n 是 2 的幂,否则,添加适当的全零行和全零列,使其变成级是 2 的幂的方阵。
将 A 和 B 都分成 4 个 (n/2)(n/2) 的方形矩阵,于是 A 和 B 就可以看成是两个以 (n/2)(n/2) 矩阵为元素的 2*2 矩阵。
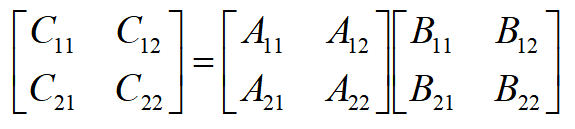
斯塔拉森算法的实现技巧
-
用 7 个乘法和 10 个加(减)法来算出下面 7 个 (n/2)*(n/2) 矩阵
-
用 8 个加(减)法算出这些 Cij。
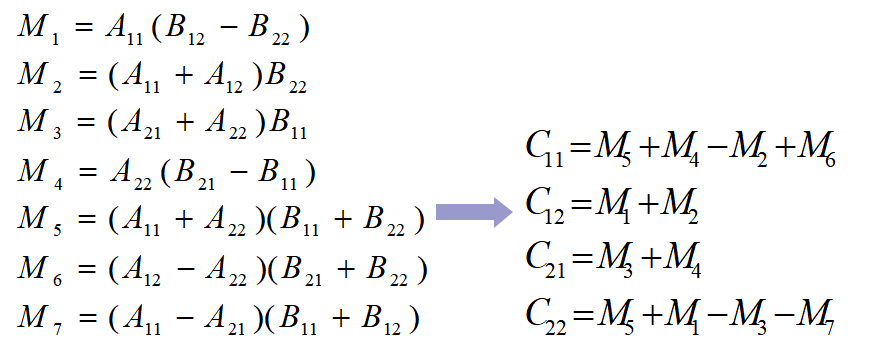
🔔 时间复杂度 O(n^2.81)
-
Hopcroft 和 Kerr 已经证明,计算 2 个 2×2 矩阵的乘积,7次乘法是必要的。因此,要想进一步改进矩阵乘法的时间复杂性,就不能再基于计算 2×2 矩阵的 7 次乘法这样的方法了。或许应当研究 3×3或 5×5 矩阵的更好算法。
-
在 Strassen 之后又有许多算法改进了矩阵乘法的计算时间复杂性。目前最好的计算时间上界是 O(n^2.376)
最大子数组
问题描述:给定一数组 A,寻找 A 中和最大的非空连续子数组。
例:数组 A = [-2, -3, 4, -1, -2, 1, 5, -3], 最大子数组应为[4, -1, -2, 1, 5],其和为7
思路:
分治法求解:假定要找出数组 A[low,high] 的最大子数组。将数组划分为规模尽量相等的两个子数组,即找到中央位置 mid,考虑求解两个子数组 A[low,mid] 和 A[mid+1,high]。
最大子数组的位置:
- 完全位于子数组
A[low,mid]中 - 完全位于子数组
A[mid+1,high]中 - 跨越了中点
可递归求解 A[low, mid] 和 A[mid + 1, high] 的最大子数组。最后考虑跨越中点的最大子数组,然后在三种情况中选取和最大者。
🌈 求跨越中点的最大子数组
procedure FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
integer left-sum, i, sum, right-sum, max-left, max-right
left-sum = -∞;
sum = 0;
for i = mid downto low
sum = sum + A[i]
if sum > left-sum
left-sum = sum
max-left = i
right-sum = -∞;
sum= 0;
for j = mid + 1 to high
sum = sum + A[j]
if sum > right-sum
right-sum = sum
max-right = j
return (max-left, max-right, left-sum + right-sum);
end FIND-MAX-CROSSING-SUBARRAY
🌈 求左/右数组的最大子数组
procedure FIND-MAXIMUM-SUBARRAY(A, low, high)
integer left-low, left-high, left-sum, right-low, right-high, right-sum, mid, cross-low, cross-high, cross-sum
if high == low
return (low, high, A[low]);
else
mid = (low + high) / 2
(left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid)
(right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid + 1, high)
(cross-low, cross-high, cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
if left-sum >= right-sum and left-sum >= cross-sum
return (left-low, left-right, left-sum)
elseif right-sum >= left-sum and right-sum >= right-sum
return (right-low, right-high, right-sum)
else return (cross-low, cross-high, cross-sum)
end FIND-MAXIMUM-SUBARRAY

最近点对问题
❓ 问题:寻找二维空间欧拉距离最近的点对。
👎 一般思路:暴力法,两个循环,依次比较每个点。时间复杂度 O(n^2)
👍 分治法


算法EfficientClosetPair(P,Q)
//输入:数组P中存储了平面上的n≥2个点,且这些点已按照x坐标升序排列
//数组Q存储了与P相同的点,只是按照点的y坐标升序排列
//输出:最近点对的欧几里得距离
If n ≤ 3 then 返回暴力法求出的最小距离
Else 将P的前n/2个点复制到PL
将PL对应的点复制到QL
将P的另外一半点复制到PR
将Q的另外一半点复制到QR
dL ← EfficientClosetPair(PL, QL)
dR ← EfficientClosetPair(PR, QR)
d=min{dL, dR}
m ←P[⌈n/2⌉].x //m为分割线
将Q中|x-m|<d 的点依次复制到数组S[num]中//num为点数
dminsq ← d^2
for i ←1 to num-1
k ←i+1,
while k ≤num and (S[k].y- S[i].y)^2 < dminsq
dminsq ← min{(S[k].x- S[i].x)^2 + (S[k].y- S[i].y)^2, dminsq}
k ← k+1
Return Sqrt(dminsq)
作业
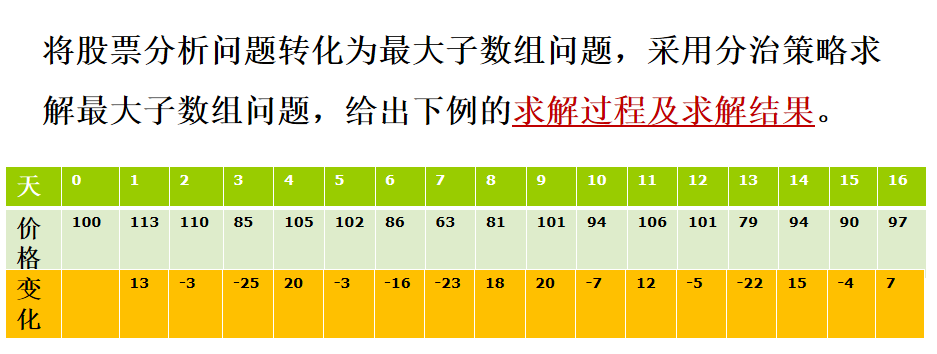

找假币问题
N个硬币放袋子里,其中一枚是假币,并且伪造的硬币比真币轻,设计一个算法找到那枚假币。要求写明算法思想,并给出算法描述(注意书写规范)。
- 如果 N 是偶数,硬币分为两半,每一半 N / 2 ,假币只可能存在于轻的一堆中,继续对轻的进行二分,直到每一半只有一枚
- 如果 N 是奇数,随便拿出一枚,剩下的硬币分为两半,若这两半一样重,则拿出的是假币;若不一样重,就对轻的继续二分。
procedure fake(coinHeap c)
if sizeof(c) % 2 == 0 then // 如果 N 是偶数
(c1, c2) = partition(c); // 硬币分为两半
lighter = cmp(c1, c2); // 假币只可能存在于轻的一堆中
fake(lighter); // 继续对轻的进行二分
else // 如果 N 是奇数
c0 = takeOne(c); // 随便拿出一枚
c = remain(c); // 剩余的硬币
if cmp(c1, c2) == 0 // 若这两半一样重
then return c0; // 则拿出的是假币
else // 若不一样重,就对轻的继续二分。
lighter = cmp(c1, c2);
fake(lighter);
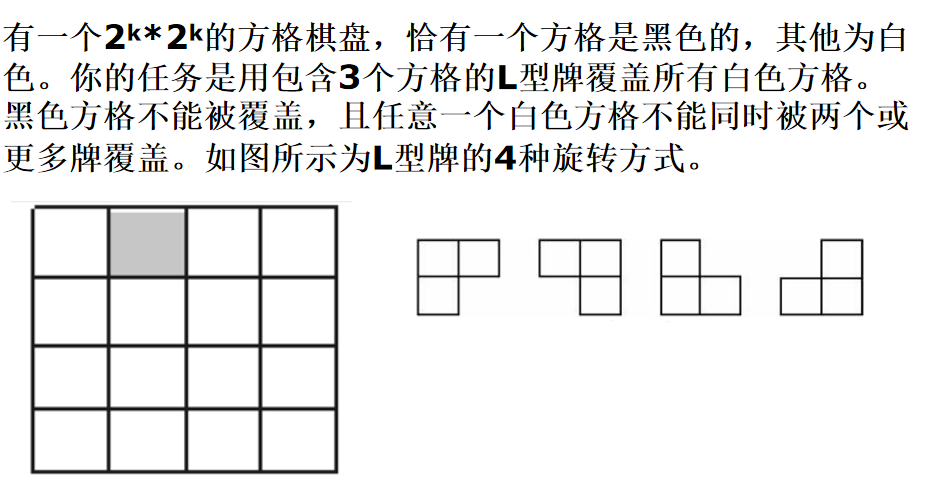
棋盘覆盖问题

贪心方法
🍎 适用条件:局部最优决策能导致产生全局最优解
背包问题的贪心(GREEDY-KNAPSACK)
// 先将物品按pi / wi比值的非增次序排序(降序)
procedure GREEDY-KNAPSACK(P,W,M,X,n)
float P(1:n), W(1:n), X(1:n), M, curLeft;
int i, n;
X <- 0;
curLeft <- M;
for i <- 1 to n do
if (W(i) > curLeft) then exit; endif;
X(i) <- 1;
curLeft <- curLeft - W(i);
repeat
if (i <= n) then X(i) <- curLeft / W(i);
endif
end GREEDY-KNAPSACK
🔔 贪心法的正确性证明





活动选择/活动安排问题
❓ 问题:有n项活动申请使用同一个礼堂,每项活动有一个开始时间和一个结束时间。同一时间只允许一个活动占用礼堂。问:如何选择这些活动,使得被安排的活动数量达到最多?
☀️ 策略:把活动按照结束时间从小到大排序,然后从前向后挑选,只要与前面选的活动相容,就可以把这项活动选入 A
算法3.3 GreedySelect
输入:活动集S,活动i的开始时间si 和结束时间fi
(i=1,2,…,n),活动按结束时间从小到大已排序;
输出:S的活动子集A
A <- {1}; j <- 1;
for i <- 2 to n do
if si ≥ fj Then A <- A ∪{i}; j <- i;
endif
Return GreedySelect
🔔 最优解的证明



带有限期的作业排序

procedure GREEDY_JOB(D, J, n)
// 作业按p1 >= p2 >= ... >= pn的次序输入;它们的期限值D(i) >= 1,1 <= i <= n,n >= 1。J是在它们的截止期限前完成的作业的集合。//
J <- {1}
for i <- 2 to n do
if (J <- {i}的所有作业都能在它们的截止期限前完成 )
then J <- J U {i}
endif
repeat
end GREEDY_JOB
☀️ 最优解证明:

分为以上四个步骤。
🔔 注意:证明之前进行一个预处理——作业 按照效益非增排序!
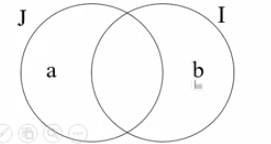
1️⃣ 证明 I、J 是互不包含关系
-
:不考虑。
-
:与 是最优解矛盾。
-
:不成立,下面进行证明。

- 是某一时刻求出的贪心解,真包含于
- 是属于 不属于 的最大效益作业
- 从左向右遍历 作业数组,遍历到 的时候贪心解为
- 则此时 。同时由于 是最优解也是可行解,可行解的子集也是可行解,所以 也是可行解,应该加入贪心解,矛盾
-
综上, 和 是互不包含关系。
2️⃣ 证明
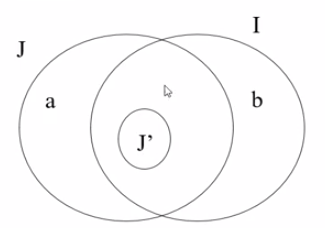
-
反证
-
设 ,并且 是 中效益最大的作业;设 ,并且 是 中的某一个作业。
-
设访问到 的时候贪心解是
-
由于 ,所以访问到 的时候所有属于 且不属于 的作业都没访问到,此时根据贪心,应该把 作为贪心解的一部分,且 是可行解 的子集,也是可行解。
-
然而事实上 并没有加入贪心解,矛盾。
-
综上,
3️⃣ 证明 中相同作业可以在同一时段调度
- 设 和 分别是 和 的可行调度表。令调度表中相同作业在相同的时间片执行,具体方法如下:
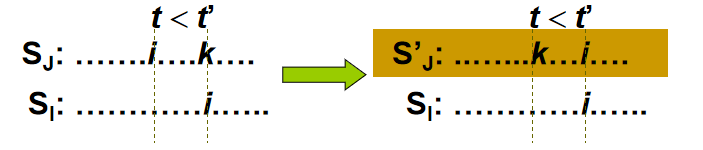
- 第一种情况: ,即 和 中相同的作业 ,在 中先发生,则在 中发生同时, 中发生的是作业 。
- 交换 中的作业 和 ,下面验证可行性:
- 中的作业 一定可以换到作业 的位置,因为在 中同一时间作业 可行。
- 中的作业 一定可以换到作业 的位置,因为 一定成立。
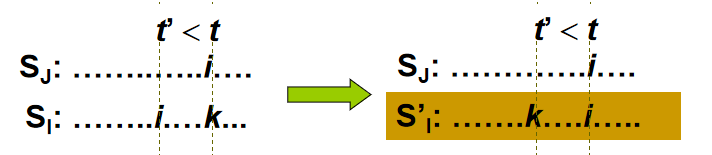
- 第二种情况: ,同理,不再赘述。
- 重复替换,指导 中相同作业在同一时段调度,形成 。
4️⃣ 同一法证明
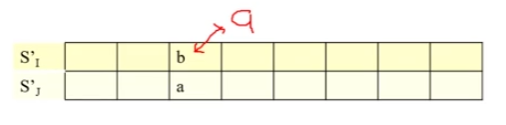
- 在 中找到第一个同一时间 不同的调度,将 中的作业 替换为 中的作业 ,下面解释可行性。
- 由于贪心性质,且时间 之前作业调度都相同,则 一定成立,保证替换之后 ,由于 是最优解,所以 。说明 也是最优解。
- 重复替换,使 在不减效益值的情况下换成 ,因此, 也必定是最优解,证毕。
☀️ 可行解判定定理证明
定理:

证明:
-
当且仅当:表示充要条件,要进行充分和必要两个证明。
-
充分证明:如果 可行,说明对于子集 有一个可行的调度方案,则 一定是可行解,显然。
-
必要证明: 同一法,若 是可行解,则 表示可以处理这些作业的一种运行的调度序列。

- 由于 可行,必然存在 ,使得 。假设 ,那么令 是使得 的最小下标。
- 显然 中一定存在 ,即 。
- 在 中将 与 交换, 一定可以换到 ,下面解释 换到 的可行性。
- 由于 中作业按照 进行排序,且 ,则 ,因为 所以 ,所以可行。
- 故作业可依新产生的排列 的次序处理而不违反任何一个期限。
- 连续使用这一方法,就可以将 转换成 且不违反任何一个期限。定理得证。
👊 快速作业排序
算法描述:对作业 i 分配时间时, 直接分配在其截止期前最靠后的空时间片,这样,避免作业移动,把 JS 的计算时间由O(n^2)降低到接近于 O(n)。
由于只有 n 个作业且每个作业花费一个车单位时间,因此只需考虑这样一些时间片 ,其中
简单来说,时间片数量=min{作业数量 n,期限 d 的最大值}。


🌈 图解:
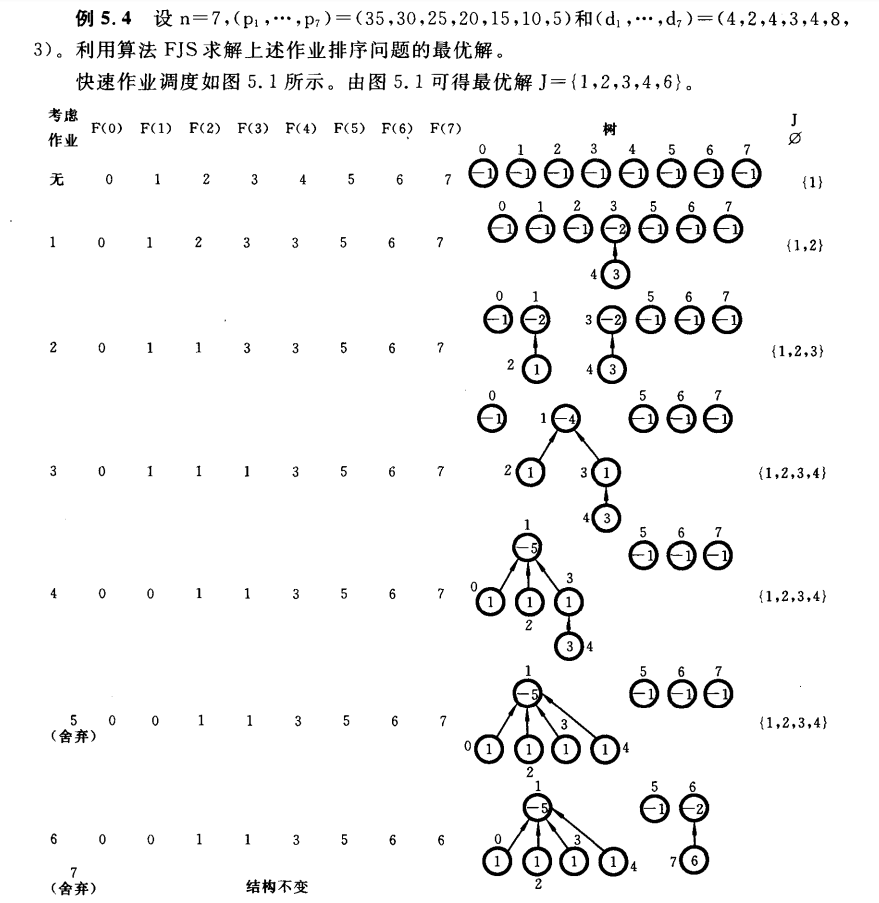
- 考虑作业的顺序按照以作业效益非增排序后的顺序为基准。(该题只是刚好排完序为1,2...)
- 增加一个 起到方便合并的作用。 初始值都是 。
- 树节点,内部数字表示根节点,外部数字表示时间片。
- 查询过程:
- 考虑作业 ,找到
- 在树中找到时间片为 的节点,如果该节点不是根节点, 向上查找的最上的祖宗节点 。
- 根据祖宗节点的时间片 查找 ,如果值为 0 则舍弃,否则将作业 添加到集合。
- 将 节点和左侧节点合并,哪个节点的子孩子多哪个节点当 ,若一样多则左侧节点当
- 更新子结点内部数字
- 更新
- 可能会进行路径压缩(第二步查找祖宗节点时,如果该节点初始不是根节点,则在查找的过程中进行路径压缩;如果该结点是根节点,则不需要进行路径压缩)
作业







动态规划
一般方法
最优性原理:无论过程的初始状态和初始决策是什么,其余的决策都必须相对于初始决策所产生的状态构成一个最优决策序列。也就是全局最优依赖于局部最优。
若多段图问题,以乘法为路径长度,当含有负权时,局部最优保证不了全局最优,最优性原理不成立;包含负长度环的任意两点间最短路径问题,最优性原理也不成立。
☀️ 最优性原理证明步骤
- 设最优决策序列形式(假设...是...的最优决策序列)
- 确定初始状态和初始决策(从...开始,已经做出了...的决策,因此...就是初始决策所产生的状态)
- 初始决策所产生的状态(如果把...看作原问题的一个子问题的初始状态,解决这个子问题就是找出...,这个决策显然是)
- 其余决策相对于③(如果不是,设...是更优决策,...,与假设矛盾,因此最优性原理成立)
🍎 适用条件
- 满足最优性原理
- 无后效性:某阶段状态决定,就不受此状态之后决策的影响
- 有重叠子问题:子问题之间不相互独立
多段图问题

☀️ 最优性原理证明
-
假设 是一条由 s 到 t 的最短路径。
-
再假设从源点 s 开始,已作出了到结点 的决策,因此 就是初始决策所产生的状态。
-
如果把 看成是原问题的一个子问题的初始状态,解决这个子问题就是找出一条由 到 t 的最短路径。
-
这条最短路径显然是
-
如果不是,设 由 到t的更短路径,则这条路径肯定比 路径短,这与假设矛盾,因此,最优性原理成立。
-
向前处理法
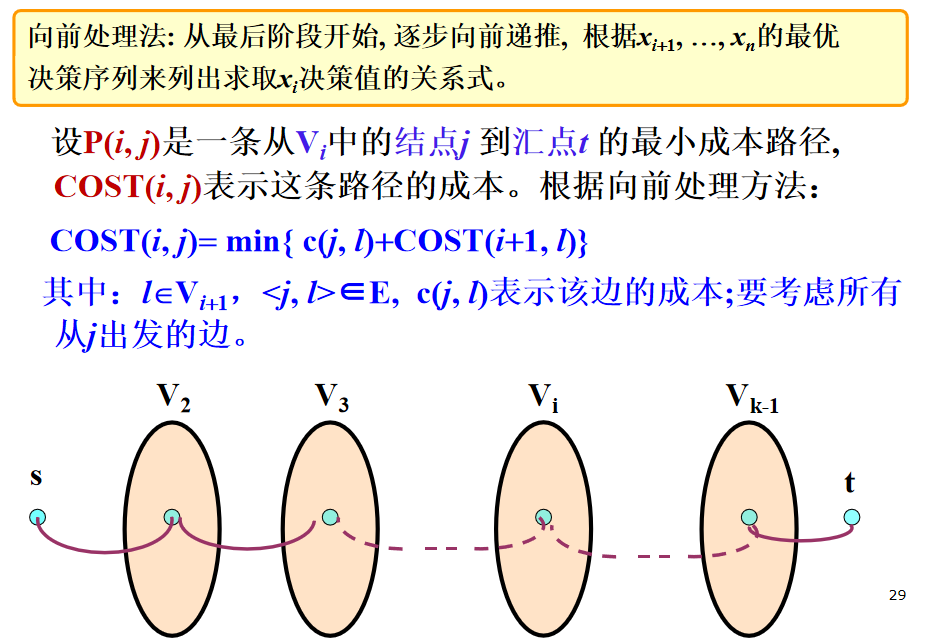
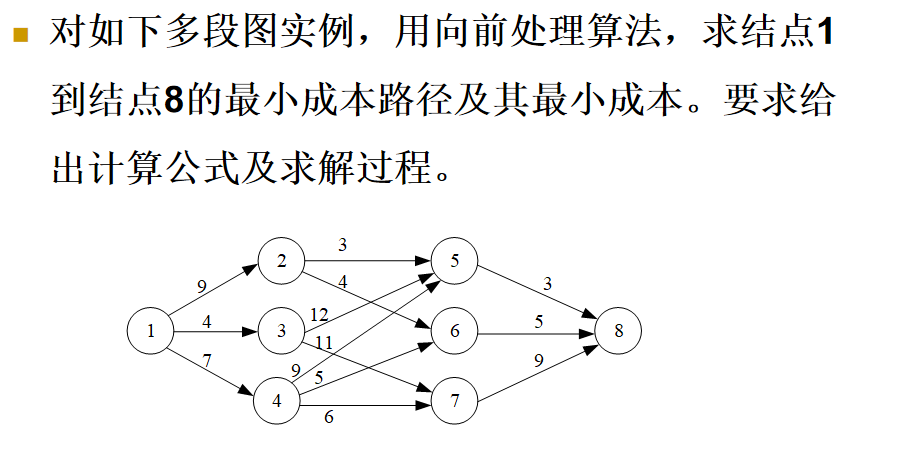
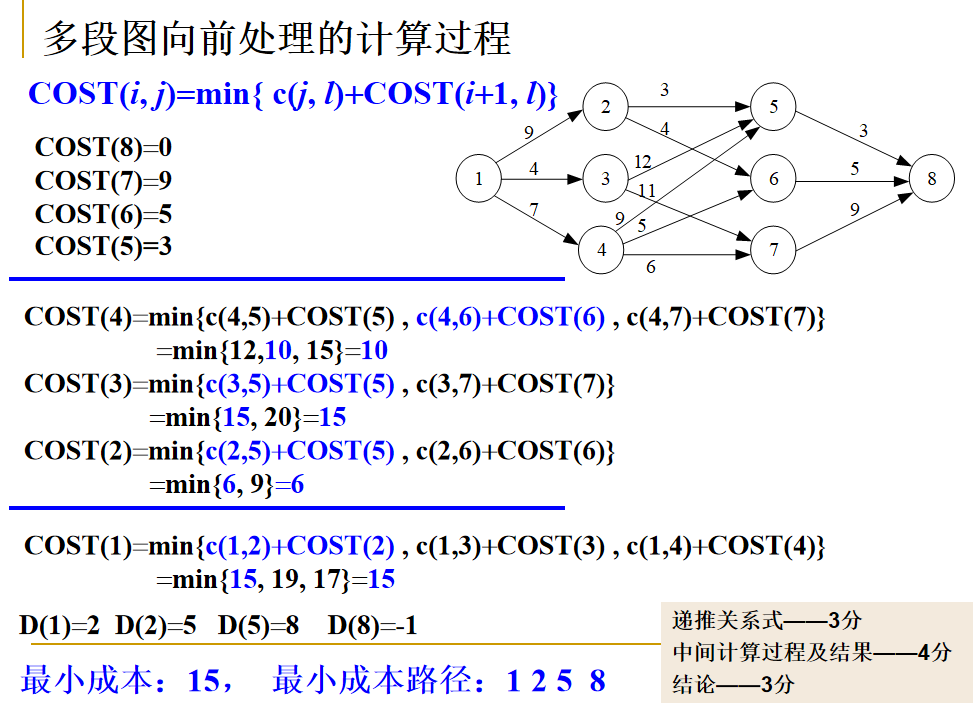
- 向后处理法
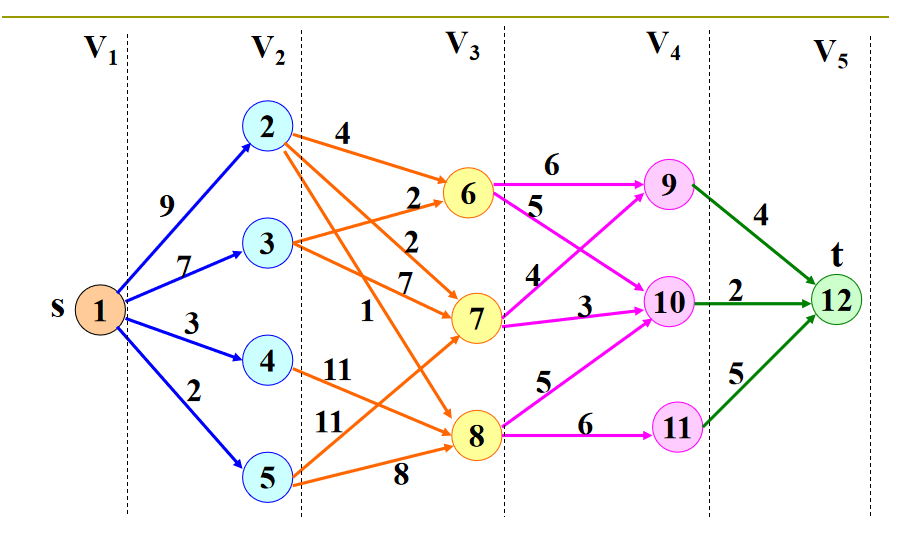
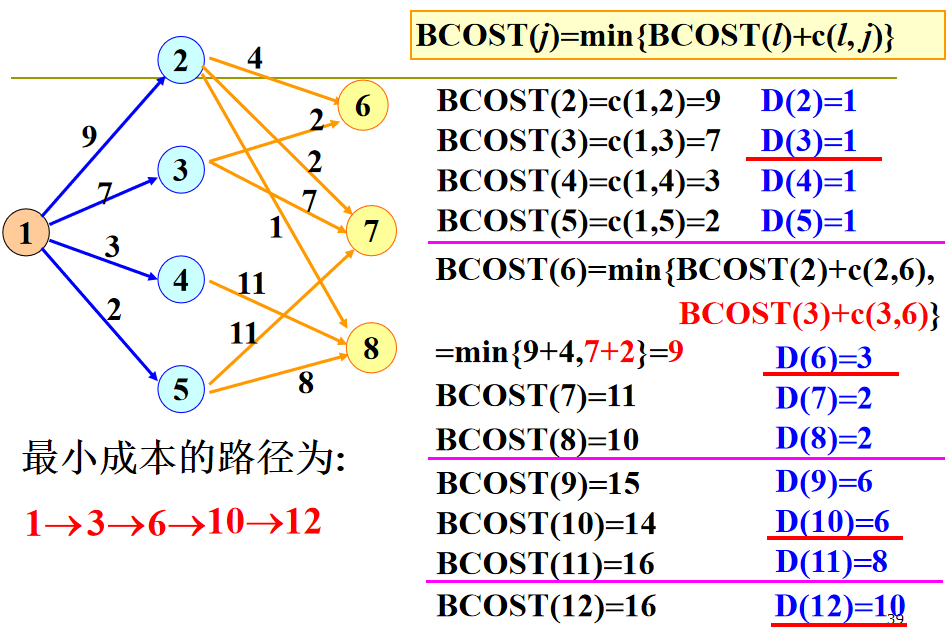
最优二分检索树
同一个标识符集合的不同二分检索树有不同的性能特征。已知一个固定的标识符集合,希望产生一种构造二分检索树的方法,使平均检索次数最小。
- 计算预期成本

- 公式推导:
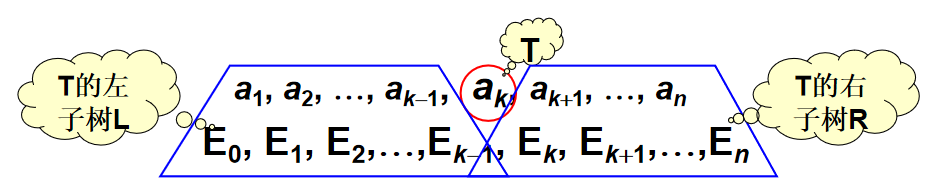
现有一棵二分检索树,根节点是 ,有 个内节点, 个外节点。(利用公式:)
左子树的预期成本是:
右子树的预期成本是:
下面想要用已经求得的左子树和右子树的预期成本公式求整棵树的预期成本:注意左右子树的高度要加一
又令
则化简为
用 表示包含 和 的最优二分检索树的成本。
初始值: 。
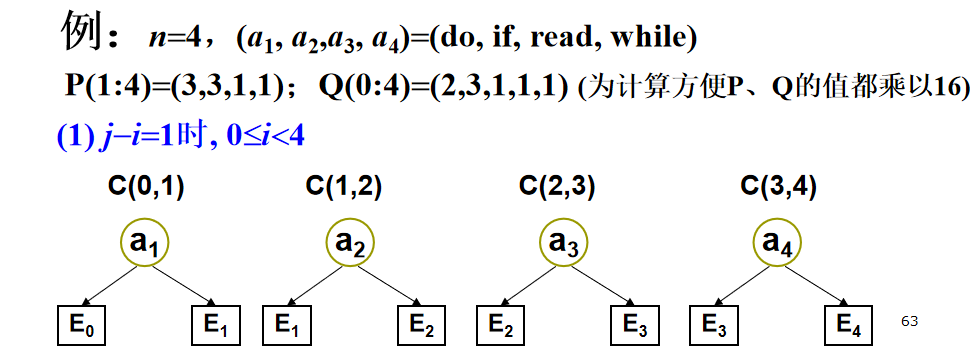




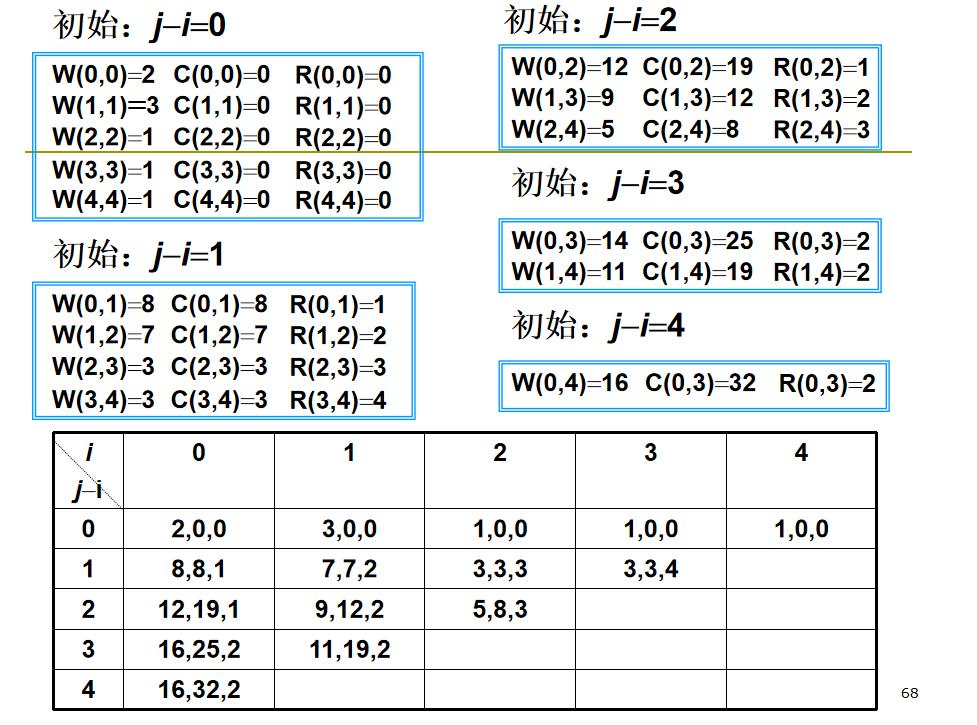
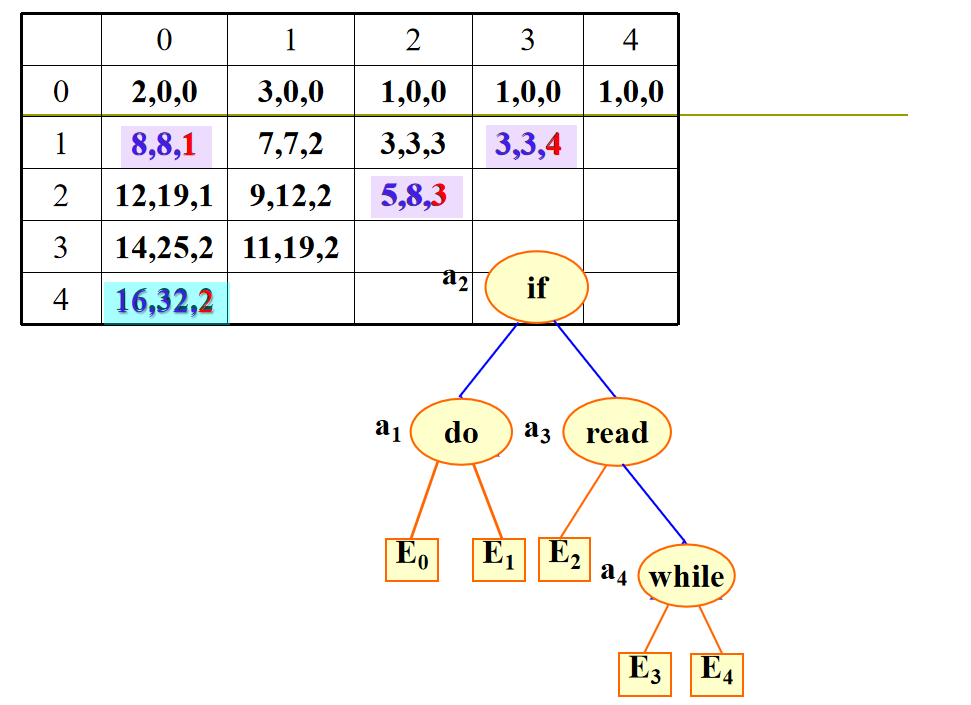
注意:最后找根节点的时候 范围是左开右闭。
构造最优二分检索树的优化算法
- 构造最优二分检索树的优化算法,把根结点 k 的检索区间限制在 R(i,j-1)≤k≤R(i-1,j),即求解的递归关系式为:

- 时间复杂度
O(n^2)
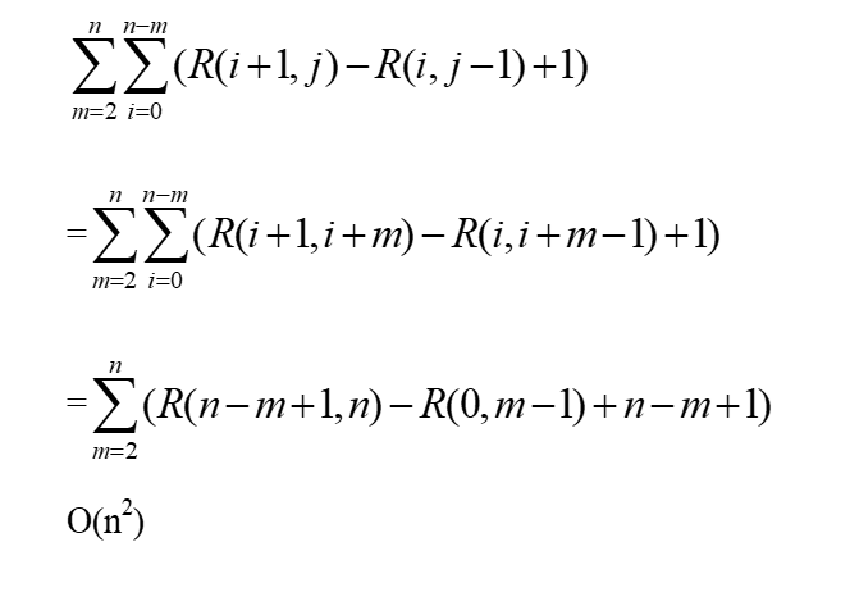
0/1背包问题
- 序偶对法


0/1背包问题出现最坏情况


流水线调度问题
基于调度规则的OFT问题


货郎担问题(旅行商)
货郎担问题:从城市 a 出发,对每个其他城市 (b,c,d,e) 都只访问一次,再回到城市 a,要求找到最短路径
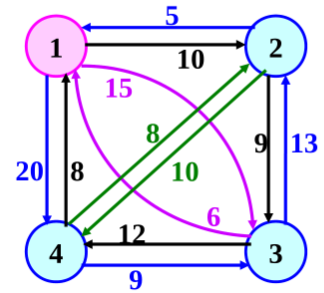
设 G(V,E) 是一个具有边成本 c 的有向图,G 的一条周游路线是包含 V 中每个结点的一个有向环,周游路线的成本是此路线上所有边的成本之和。
☀️ 证明最优性原理:
- 假设周游路线是开始于结点 1 并终止于结点 1 的一条简单路径(所有节点之经历一次)
- 每一条周游路线都是由一条边 <1,k> 和一条由结点 k 到结点 1 的路径所组成的,其中k V-{1}。
- 这条由结点 k 到结点 1 的路径通过 V-{1,k} 的每个结点各一次。如果这条周游路线是最优的,则这条由 k 到 1 的路径必定是通过V-{1,k} 中所有结点的由 k 到 1 的最短路径,因此最优性原理成立。
🌋 递推公式:
- :表示从节点 i 出发经过集合 S 中所有节点一次到达节点 1 的最小成本
- 递推的时候需要遍历集合 S 中的所有节点,找到最小成本路线
- 初始时,集合 S 为空集,节点 i 到节点 1 的成本就是两点之间的距离
- 依次求出 的所有 ,k=0,1...n-1
- 当 时,, 且
- 当 时,求 ,问题得解
🐍 模拟过程:
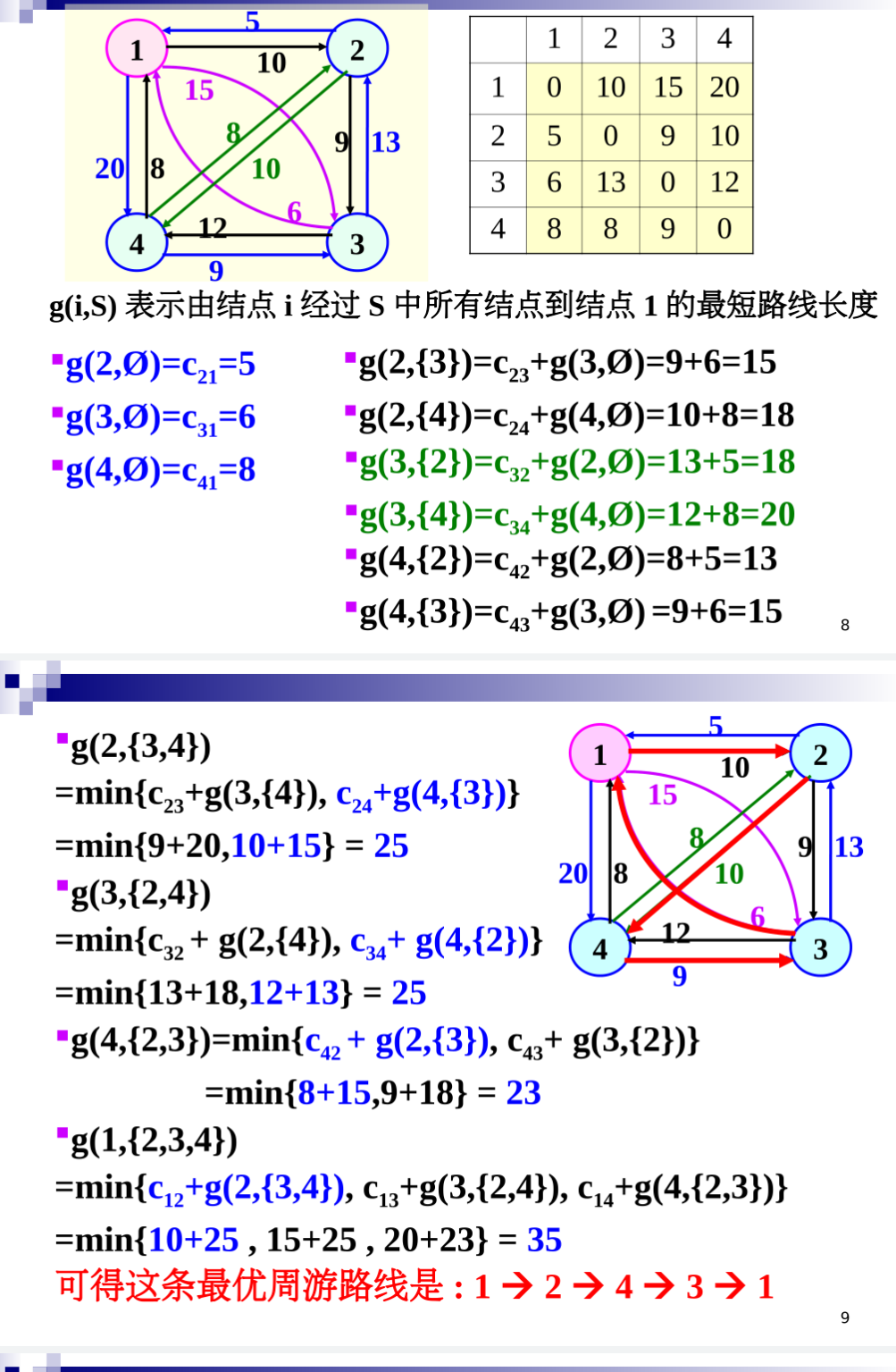
🍎 复杂度分析:

🍑 代码:

作业
找零钱问题——递推关系式

币值最大化问题(打家劫舍问题)

-
-
初始 ,然后依次求出 到
-
过程
-
序列为
回溯法
一般方法
搜索算法通过系统的搜索(或遍历)给定问题的解空间来确定问题的解。解空间也称为搜索空间。解空间可以用树结构加以描述。
搜索问题往往对解设定约束条件,满足约束条件的解称为可行解。搜索任务往往是找到一个或所有可行解。
组合优化问题:带有目标函数,求解的目的是找到 ①满足约束条件 ② 使目标函数达到最大(或最小)的解,称为最优解。求解组合优化问题,任务是找最优解。
解空间树:搜索空间具有一定的结构,通常是树形结构,我们把这样的树形结构称为“解空间树”;解空间树并不真实存在,只是我们在构造算法时设想出来的,为了使算法构造过程更加清晰。
解空间树、状态空间( space)树:整棵树,包括所有结点,及由根到各结点的路径。
问题状态(problem state):树中的结点,表示所求解问题(或子问题)的状态。
解状态(solution states): 树中的结点,由根到解状态的路径确定了解空间的一个完整元组。
答案状态(answer states): 是这样的一些解状态S,由根到S的这条路径确定了问题的解(解决方案)。
算法的目标就是搜索整棵状态空间树,去找答案结点。
限界函数(规范函数):用来判断该结点是否满足约束条件,其子树是否可能包含答案结点;
回溯法的解需要满足一组综合的约束条件,通常分为显式约束和隐式约束。
- 显式约束条件: 限定每个x只从一个给定的集合上取值。显式约束条件确定了解空间的结构,一般与具体问题实例无关。
- 隐式约束条件: 规定了实例的解空间中那些满足规范(限界)函数的元组,描述了 彼此相关的情况。
解空间中满足隐式约束条件的元组称为可行解。
回溯法是一个既有系统性又有跳跃性的搜索算法。
- 系统性是指搜索规则在解空间树中,按深度优先策略,从根结点出发搜索解空间树。
- 跳跃性是指未必搜索解空间树中所有结点,当搜索到某一结点时,先判断该结点是否可能到达答案结点:
- 如果不能到达,则跳过以该结点为根的子树,向上回溯;
- 否则,进入该子树,继续按深度优先策略搜索。
用回溯法求问题的所有解,需要把整棵解空间树都搜索遍才结束。
用回溯法求问题的一个解,只要搜索到一个解即可结束算法。
这种以深度优先方式系统搜索问题解的算法,称为回溯法。
活结点:一个结点如果已被生成,而它的所有儿子结点还没有全部生成,则称这个结点为“活结点”;表示开始处理但还没有完全处理完毕的结点;活结点不只一个,需要活结点表存储。
死结点:其儿子已全部生成或在该结点剪枝,从而无需向下扩展的结点,称为“死结点”,表示已经处理完毕的结点。
E结点:当前正在生成其儿子结点的活结点,称为“E-结点”(正在扩展的结点),即正在处理的结点,同一时刻只有一个E结点。
回溯法搜索过程
- 首先,根结点为活结点, 也为当前扩展结点(E结点)。
- 在E结点处, 搜索向纵深方向移至一个新结点, 该新结点成为一个新的活结点, 并成为E结点,并继续进行该操作,直到在E结点处不能再向纵深方向移动, 则该E结点成为死结点。
- 此时,回退至最近的一个活结点处, 并使该活结点成为E结点,继续执行第②步。
- 回溯法以这种方式递归地在解空间中搜索, 直至找到所要求的解或解空间中没有活结点为止。
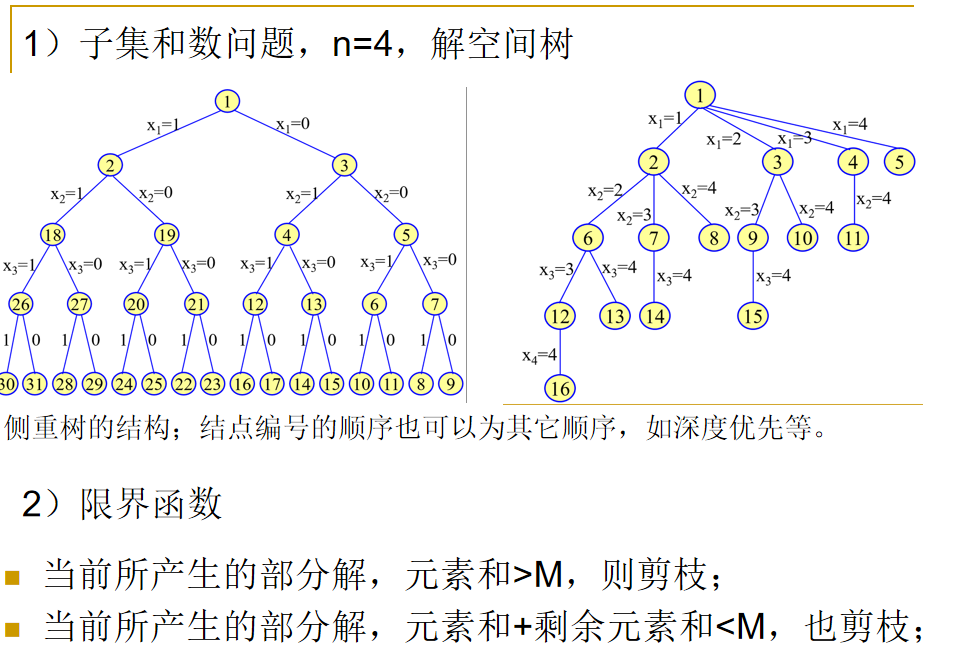
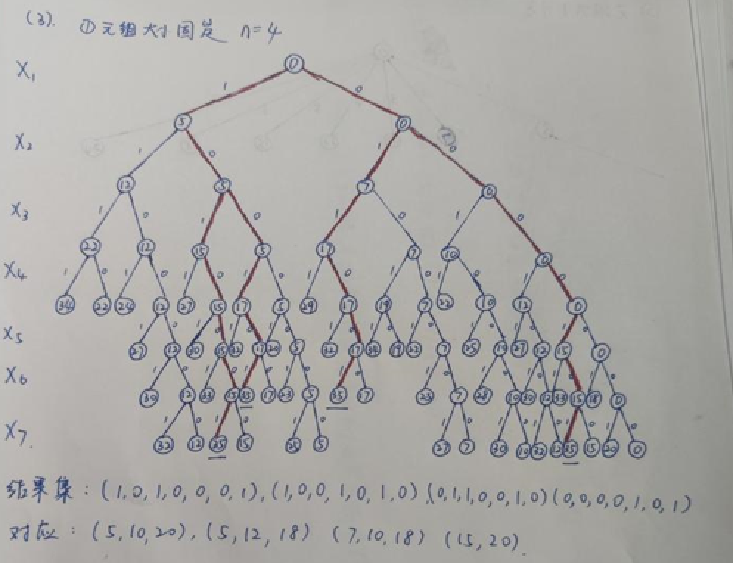
子集和问题

1️⃣ n 元组

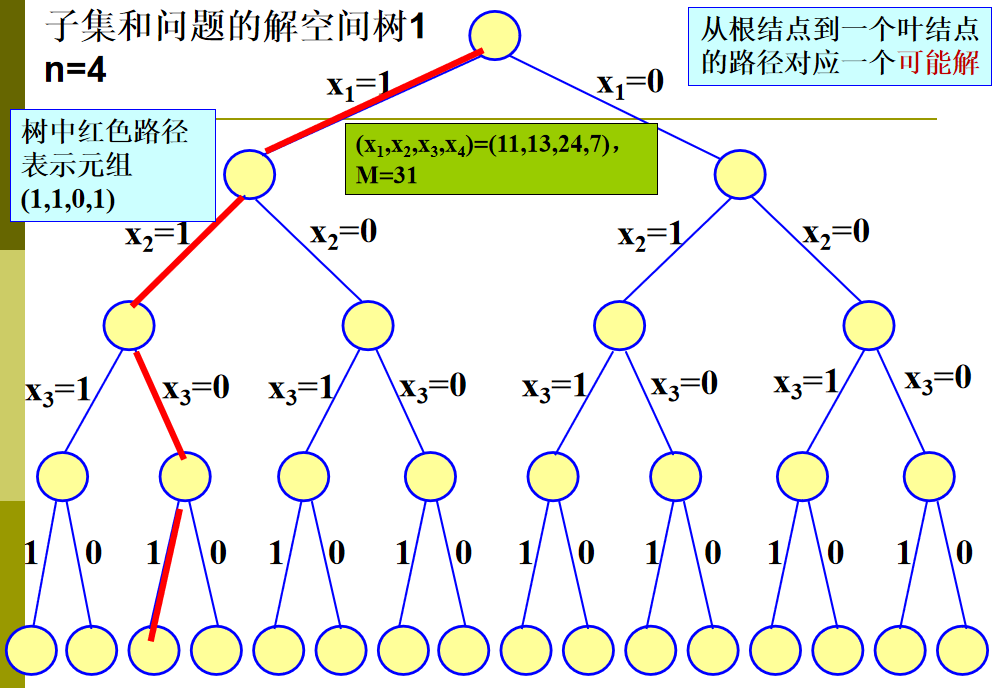
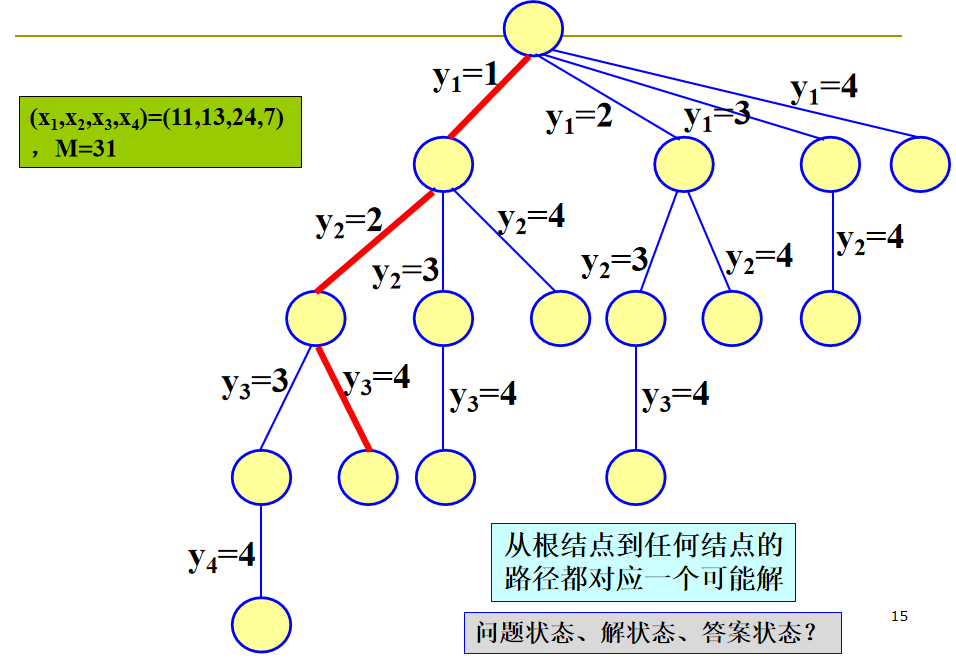
2️⃣ k 元组

八皇后
🌈 四皇后解空间树
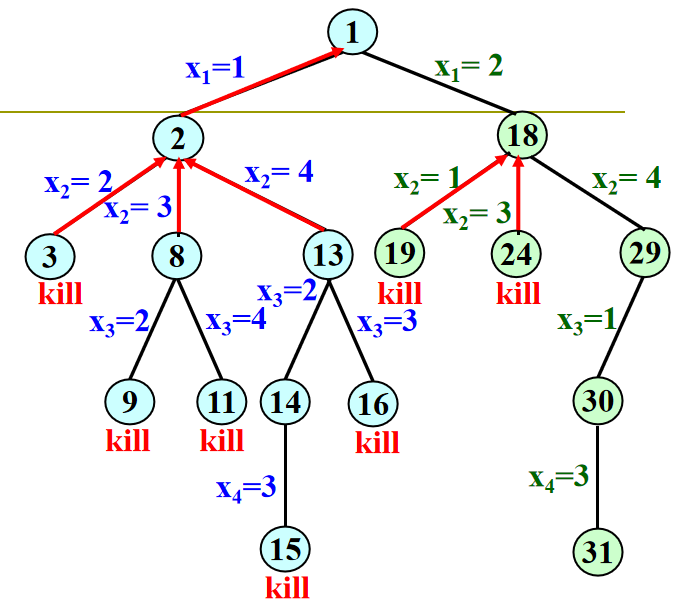
限界函数:
PLACE(k):
令X(k)与X(i)逐个比较,i=1..k-1。
若存在X(k)=X(i)或者|X(i)-X(k)|=|i-k|
则返回false;
否则返回true。
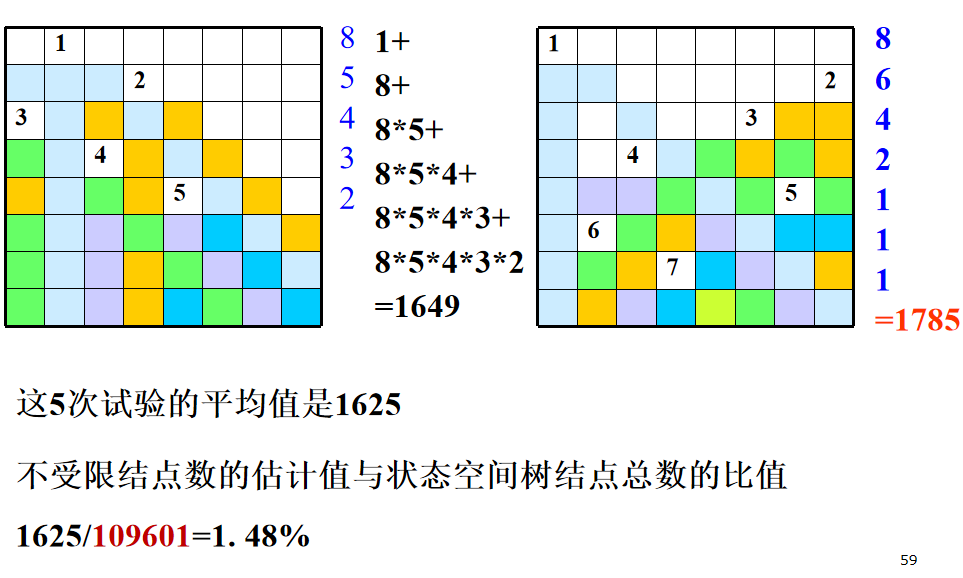
8-皇后问题不受限结点数的估计值
回溯法效率分析

数独游戏
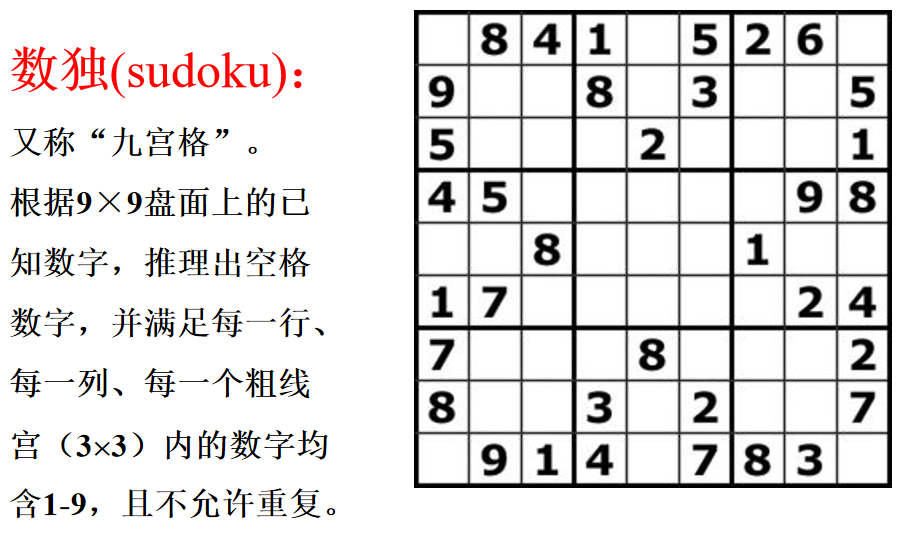
- 解空间树结构:九叉树
- 限界条件:行不重,列不重,对角线不重
class Solution {
public void solveSudoku(char[][] board) {
dfs(board);
return;
}
public boolean dfs(char[][] board) {
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
if(board[i][j] != '.') continue;
for(char k = '1'; k <= '9'; k++) {
if(isValid(board, i, j, k)) {
board[i][j] = k;
if(dfs(board)) return true;
board[i][j] = '.';
}
}
return false;
}
}
return true;
}
public boolean isValid(char[][] board, int row, int col, char c) {
// 行不重
for(int i = 0; i < 9; i++) {
if(board[row][i] == c) return false;
}
// 列不重
for(int i = 0; i < 9; i++) {
if(board[i][col] == c) return false;
}
// 对角线不重
int startX = row / 3 * 3;
int startY = col / 3 * 3;
for(int i = startX; i < startX + 3; i++) {
for(int j = startY; j < startY + 3; j++) {
if(board[i][j] == c) return false;
}
}
return true;
}
}
作业


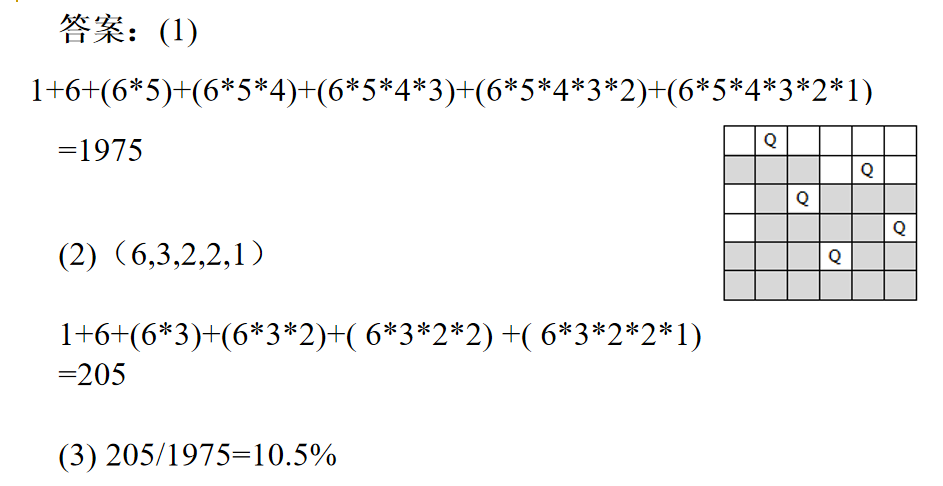
分支限界法
一般方法
- 分支限界法类似于回溯法,也是一种在问题的解空间树上搜索问题解的算法。
- 回溯法与分支限界法,解空间树的构造都是从根结点开始,按照某种次序生成其他结点。
- 两者本质差别是搜索策略/结点生成次序不同:
- 回溯法: 深度优先次序
- 分支限界法:广度优先、D检索、智能序。
- 搜索算法的求解任务与目标:
- 找出解空间树中满足约束条件的一个解或所有解;
- 在满足约束条件的解中找出使得某一目标函数达到极大或极小值的解,即某种意义下的最优解。
- 回溯法侧重找可行解——系统地搜索;
- 分支限界法找可行解和最优解——以最快速度、最小成本搜索。
- 分支限界法
- 当前E-结点要生成其全部子结点,该结点变为死结点,子结点进入活结点表后,再从中选一个作为新的E-结点;
- 使用限界函数进行剪枝,帮助避免生成不包含答案结点子树的状态空间。
- 根据状态空间树中结点检索次序的不同,将其分为:
- FIFO检索,活结点表采用一张先进先出的表(队列)
- LIFO检索,活结点表采用一张先进后出表(堆栈)
- 对下一个E结点的选择规则是死板、盲目的。
- 对于可能快速检索到答案结点的结点没有给出任何优先权。于是提出 LC 检索
LC-检索(最小成本检索)
对活结点使用一个“有智力的”排序函数 c(.) 来选取下一个 E 结点,以加快到达答案结点的速度。从上帝视角(理想状态下)定义一个结点成本函数 c(X)
- 如果 X 是答案结点,则 c(X) 是由根结点到 X 的成本(即所需的代价,可以是级数、时间开销等);
- 如果 X 不是答案结点,但子树 X 中包含答案结点,则 c(X) 等于子树 X 中(具有最小成本的)答案结点的成本;
- 如果 X 不是答案结点且子树 X 不包含任何答案结点,则 c(X)=∞;
节点估计函数:ĉ(X) = f(h(X)) + ĝ(X)
-
ĉ(X):成本估计
-
h(X):根结点到结点 X 的成本
-
ĝ(X):结点 X 到一个答案结点的估计成本
-
函数 f 是一个非降函数,其作用为调整 h 和 ĝ 在成本估计函数 ĉ 中的影响比例。
LC检索(Least Cost search):选取成本估计函数ĉ值最小的活结点作为下一个E结点。
伴有限界函数的LC检索称为LC分支限界检索。
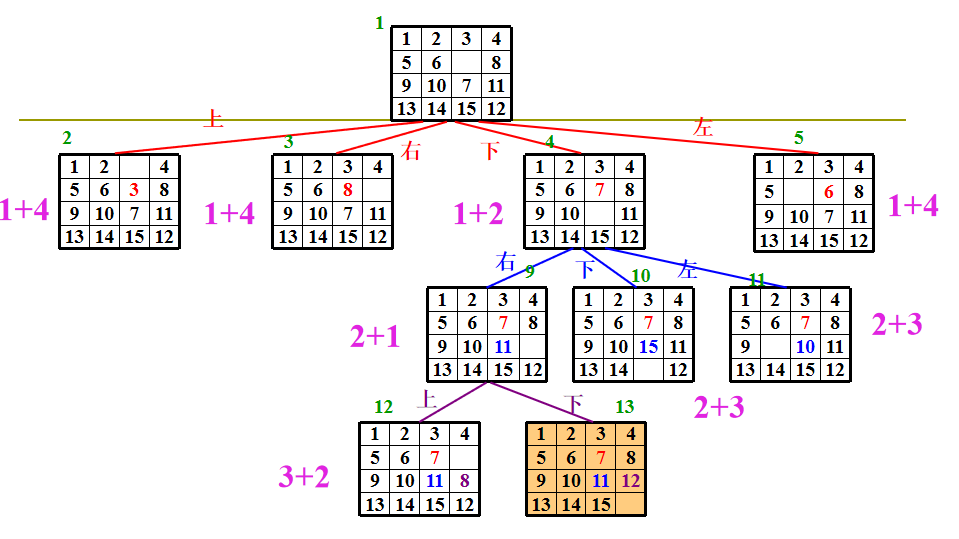
LC检索例:15-谜问题

初始状态能否到达目标状态
- POSITION(i) 是编号为 i 的牌在初始状态下的位置号,1 i 16。POSITION(16) 表示空格的位置。position(1)=1, position(3)=2, position(4)=3,position(15)=4,,position(16)=6
- LESS (i) 是满足牌 j < 牌 i ,且POSITION(j) > POSITION(i) 的牌 j 的数目。即在初始排列中找到后面比自己大的。
- 初始状态下,如果空格在下图的阴影位置中的某一格处,则令X=1;否则X=0。
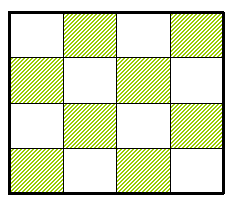
- 当且仅当 是偶数时初始状态能到达目标状态。
🐍 举例:

计算过程
- 验证初始状态能否到达目标状态
- 成本估计函数 ,:由根到结点X的路径长度, :以X为根的子树中由X到目标状态的一条最短路径长度的估计值(即 ĝ(X) =不在其目标位置的非空白牌数目)。
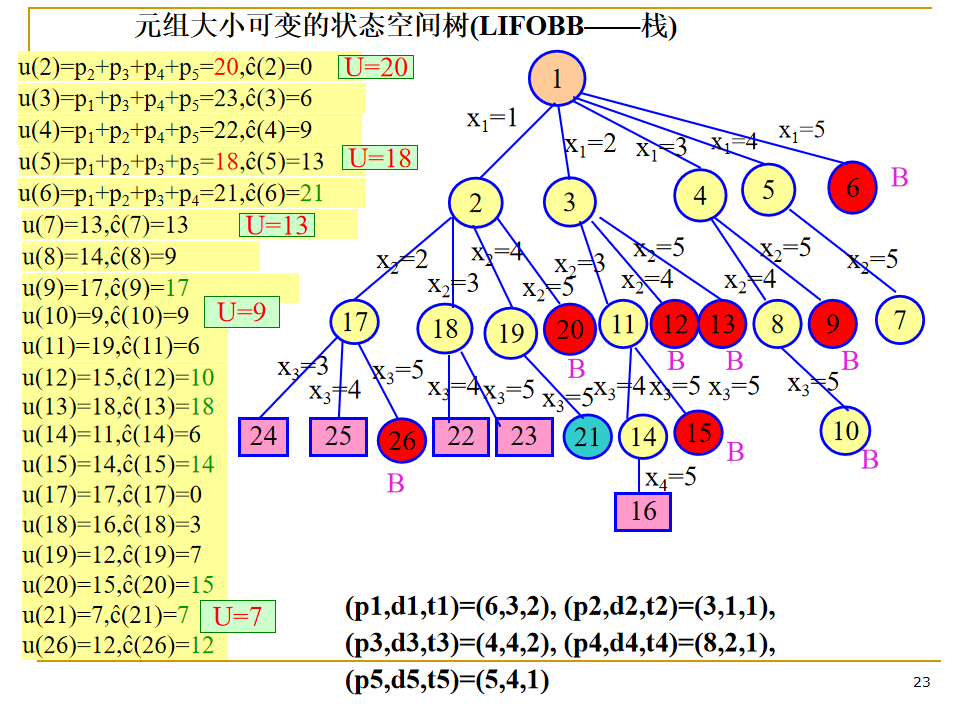
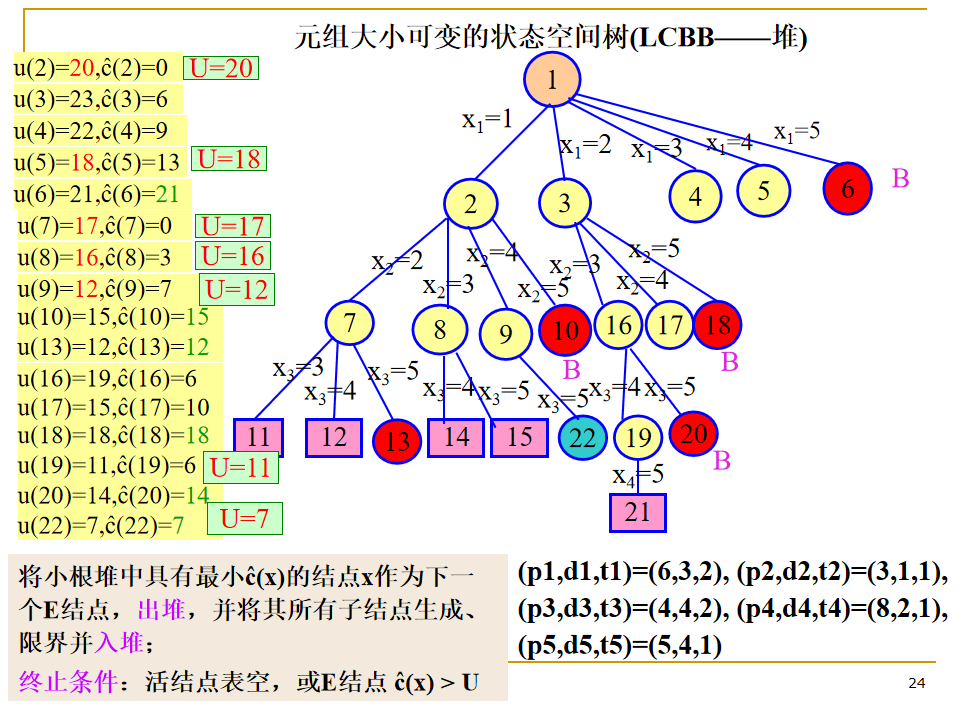
带限期的作业排序问题

- :惩罚值
- :期限。如果期限内未完成,则交罚款。
- :作业 i 的处理时间

- u(X):最大惩罚值,即所有未被选取的作业的惩罚值之和。
- ĉ(X):被舍弃的作业的惩罚值之和。
- 注意有的作业一开始就放不进去。每次处理作业时要先考虑是否还能处理当前节点!,综合考虑期限和作业处理时间。

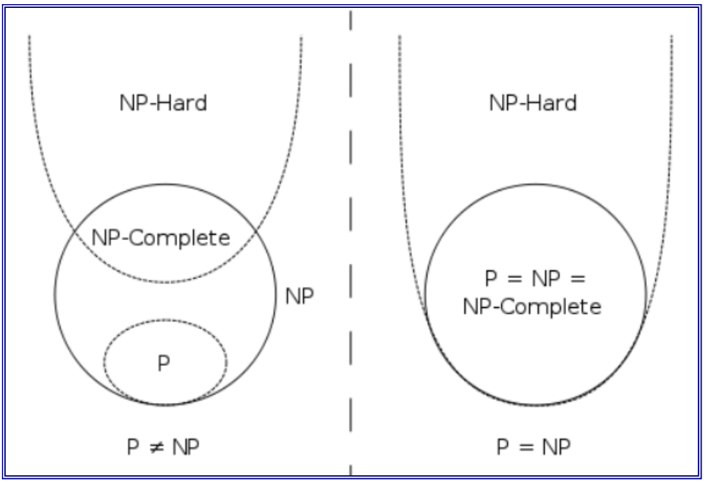
NP问题
易解问题与难解问题
可以在多项式时间内求解的问题,称为易解的(tractable),不能在多项式时间内求解的问题,称为难解的(intractable);
P与NP问题
-
P 类问题
- 定义:所有多项式时间内可解的判定问题所构成的问题集合,称为“P类”问题;
一个判定问题是易解的,当且仅当它属于P类问题;
- 定义:所有多项式时间内可解的判定问题所构成的问题集合,称为“P类”问题;
-
NP 问题(Non-deterministic polynomial)
- 定义:是所有可在多项式时间内用不确定算法验证的判定问题的集合。
-
P 与 NP 的关系
- 所有的P类问题都是NP问题
- 若其中一个问题获得多项式算法,则这一类问题就全部获得了多项式算法;反之,若能证明其中一个问题是多项式时间内不可解的,则这一类问题就全部是多项式时间内不可解的。这类问题将称之为NP完全(NPC)问题。
- NP完全问题(NPC问题):如果所有NP问题都能通过一个多项式时间算法转换为某个NP问题,那么这个NP问题就称为NP完全问题。
- 同时满足下面两个条件的问题就是NPC问题:1)它得是一个NP问题;2)所有的NP问题都可以规约到它。
- 第一个被证明是NPC问题的是可满足性问题(SAT问题)
-
COOK定理:任何 NP 问题都可以在多项式时间内转化为为可满足性问题。可满足性在P内,当且仅当P=NP -
NP-Hard问题:NPC问题规约到它,NP-Hard问题要比NPC问题更复杂,范围更广,甚至难度超越NP范畴。不一定是 NP 问题
本文作者:GHR
本文链接:https://www.cnblogs.com/gonghr/p/16485895.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
2021-07-17 【分布式】CAP理论及其应用