数据库系统原理「通关指南」

数据库概述（Introduction）

什么是数据库管理系统

  • Database Management System (DBMS)
  • 数据 + 管理系统

数据库存在的价值

  • Data redundancy and inconsistency（冗余与不一致性）
  • Difficulty in accessing data （获取数据困难）
  • Data isolation （数据孤岛）
  • Integrity problems （完整性问题）

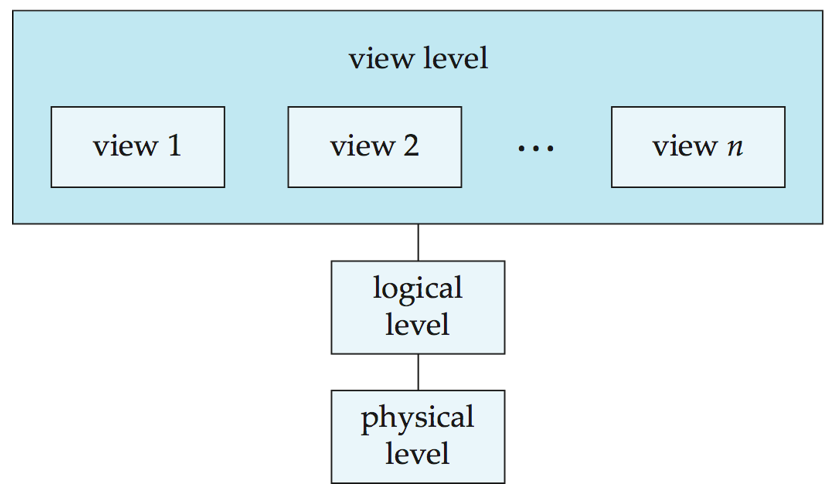
数据库的三层抽象

  • 物理层（Physical level）：最低层次的抽象，描述数据实际上是怎样存储的。物理层详细描述复杂的底层数据结构。
  • 逻辑层（Logical level）：比物理层层次稍高的抽象，描述数据库中存储什么数据及这些数据间存在什么关系。这样逻辑层就通过少量相对简单的结构描述了整个数据库。虽然逻辑层的简单结构的实现可能涉及复杂的物理层结构，但逻辑层的用户不必知道这样的复杂性。这称作物理数据独立性( physical data independence)。数据库管理员（DBA）使用抽象的逻辑层，他必须确定数据库中应该保存哪些信息。
  • 视图层（View level）：视图层(view level)。最高层次的抽象，只描述整个数据库的某个部分。尽管在逻辑层使用了比较简单的结构，但由于一个大型数据库中所存信息的多样性，仍存在一定程度的复杂性。数据库系统的很多用户并不需要关心所有的信息,而只需要访问数据库的一部分。视图层抽象的定义正是为了使这样的用户与系统的交互更简单。系统可以为同一数据库提供多个视图。

实例与模式

  • 实例（Instances）：指特定时刻存储在数据库中的信息的集合

  • 模式（Schemas）：指数据库的总体设计

    • 物理模式（physical schemas）：在物理层描述数据库的设计
    • 逻辑模式（logical schemas）：在逻辑层描述数据库的设计。程序员使用逻辑模式来构造数据库应用程序
    • 子模式（subschemas）：描述了数据库的不同视图

数据模型（Data model）

  • 关系模型（retional model）：用表的集合来表示数据和数据间的联系
  • 实体-联系模型（entity-relationship model）：基于对现实世界的认识——现实世界由一组称作实体的基本对象以及这些对象间的联系构成。广泛用于数据库设计
  • 基于对象的数据模型（object-based data model）：基于面向对象设计思想
  • 半结构化数据模型（semistructured data model）：可拓展标记语言 xml，eXtensible，Markup，Language

数据库构成（Database System Internals）

数据库架构（Database Architecture）

  • Centralized （集中式）
  • Client-server （客户/服务器式）
  • Parallel (multi-processor) （并行）
  • Distributed （分布式）

关系型数据库概述（ Intro to Relational Model）

关系 （Relation）

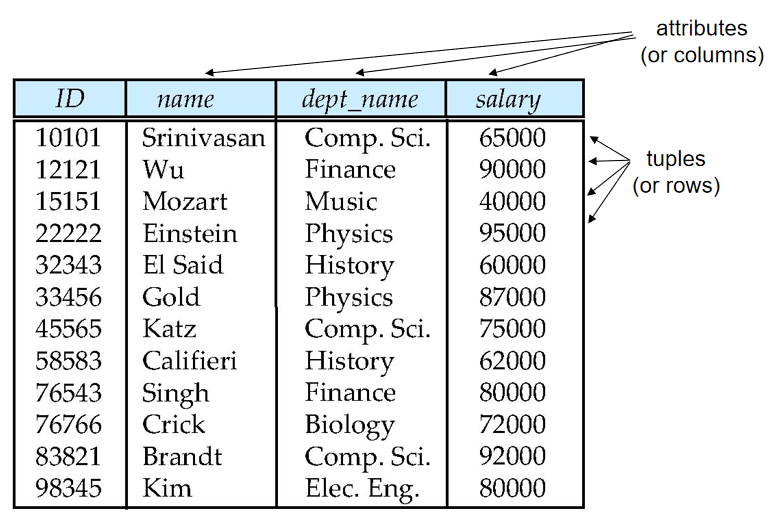
  • 属性（attributes）：表中每一列数据。A1, A2, …, An
  • 元组（tuples）：表中每一行数据
  • 关系（relation）：关系是无序的
    • 关系实例（relation instance）：表
    • 关系模式（relation schema）： R = (A1, A2, …, An )。例如： instructor = (ID, name, dept_name, salary)

码/键（keys）

  • 超码（super key）：一个或一组属性，能够唯一区分一个关系的任何一个元组。例如 {ID, name}，{ID}

  • 候选码（candidate key）：最小的（包含属性个数最少）超码。例如 {ID}

  • 主码（primary key）：候选码中挑出一个作为主码，任何关系只能有一个主码

  • 外码（foreign key）：一个表中某一列的所有值一定出现在另一张表的某一列，且在另一张表中为主码

大学数据库模式图

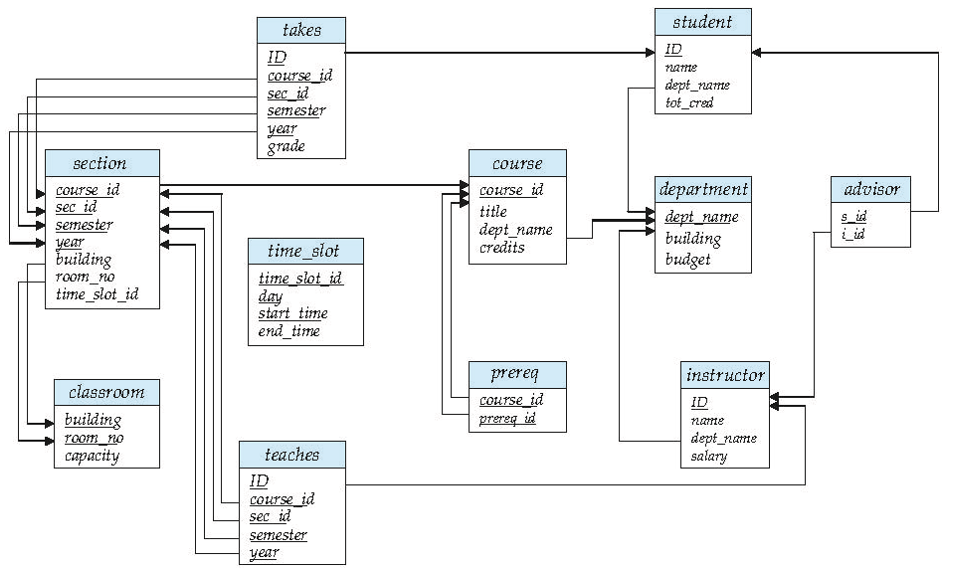
image-20220710184350453

department(dept_name,building,budget);
instructor(ID, name,dept_name,salary);
course(course_id,title,dept_name,credits);
section(course_id,sec_id,semester,year,building,room_number,time_slot_id);
teaches(ID,course_id,section_id,semester,year);
student(ID,name,dept_name,tot_cred);
prereq(course_id,prereq_id);
Advisor(s_id,i_id)
takes(ID,course_id,sec_id,semester,year,grade)
classroom(building,room_number,capacity)
time_slot(time_slot_id,day,start_time,end_time)

大学数据库 E-R 图

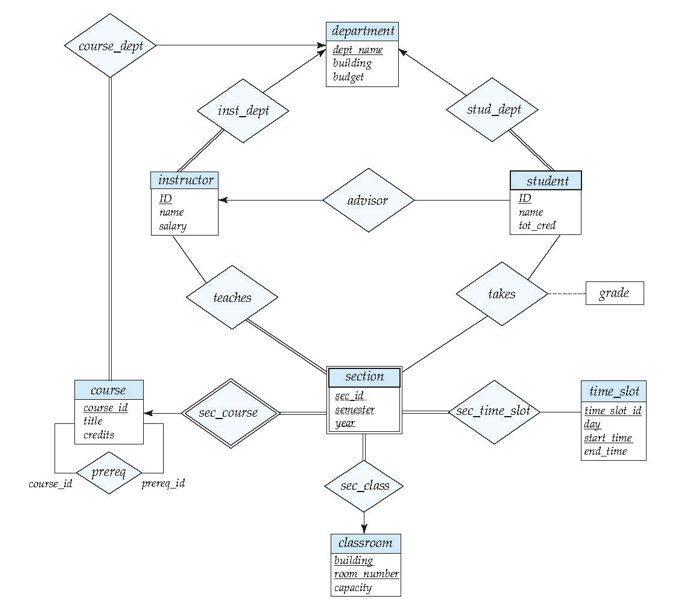
形式化关系查询语言（ Formal Relational Query Languages ）

关系代数（Relational Algebra）

1️⃣ 选择（Select Operation）

  • 定义：$ \sigma _p (r)$ = {t | t $ \in $ r and p(t)}，p 是谓词，选择出满足谓词的元组

  • 例题：

    • 选出物理系或者年薪资大于70000美元的老师：$ \sigma _{dept_name=''Physics'' \lor ,,salary>70000}\left( instructor \right) ,,$
    • 选出除了物理和计算机学院之外的老师：$ \sigma _{dept_name\ne ''Physics'' \land ,,depe_name\ne ''Comp.Sci.''}\left( instructor \right) $

2️⃣ 投影（Project Operation）

  • 定义：$ \prod\nolimits_{A_1,A_2,...,A_k}^{}{\left( r \right)}$，选出特定的属性，结果只包含这 k 列，其他列不显示

  • 例题：

    • 找出所有计算机学院的老师的姓名：$ \prod\nolimits_{name}^{}{\left( \sigma _{\mathrm{de}pt_name=''Comp.Sci.''}\left( instructor \right) \right)}$

3️⃣ 集合并（Union Operation）

  • 定义： r $ \cup $ s = {t | t $\in $ r or t $ \in $ s}，两表查询结果合并

  • 要点：

    • r ，s 必须包含相同属性，即同元
    • r ，s 属性的域必须相容

  • 例题：

    • 找出所有在 2018 年秋季或者在 2019 年春季开课的课程：

      \[\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=''Fall'' \land \,\,year=2018}\left( \sec tion \right) \right) \cup}\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=''Spring'' \land \,\,year=2019}\left( \sec tion \right) \right)} \]

4️⃣ 集合差（Set Difference Operation）

  • 定义：r - s = {t | t $ \in $ r and t \(\notin\) s}，查询出属于 r 但不属于 s 的元组

  • 要点：

    • r ，s 必须包含相同属性，即同元
    • r ，s 属性的域必须相容

  • 例题：

    • 找出所有在 2018 年秋季但不在 2019 年春季开课的课程：

      \[\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=''Fall''\land \,\,year=2018}\left( \sec tion \right) \right) -}\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=''Spring''\land \,\,year=2019}\left( \sec tion \right) \right)} \]

5️⃣ 笛卡尔积（Cartesian-Product Operation）

  • 定义：r $ \times $ s =

  • 要点：

    • 笛卡尔积之后形成的新表要改名
    • 注意两表中相同属性命名使用 表名.属性名 或其别名

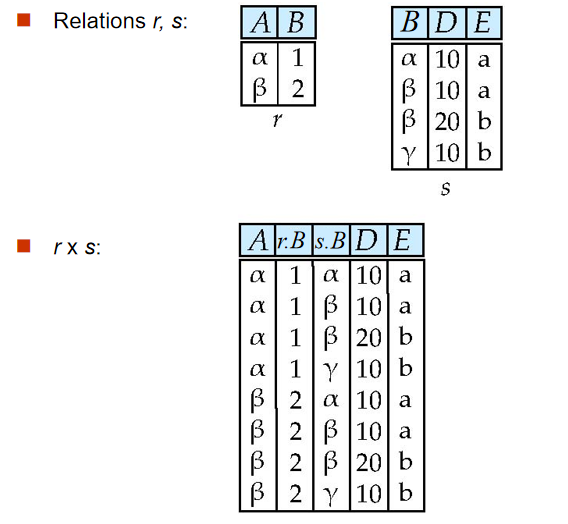
  • 例题：

    • 选出计算机学院所有学生的选课信息

      先笛卡尔积再选择：$ \sigma _{dept_name='Comp.Sci.'}\left( \sigma _{student.ID=takes.ID}\left( student\times takes \right) \right) $

      先选择在笛卡尔积：$ \sigma _{student.ID=takes.ID}\left( \sigma _{dept_name='Comp.Sci.'}\left( student \right) \times takes \right) $

6️⃣ 更名（Rename Operation）

  • 定义：$ \rho _{x\left( A_1,A_2,...,A_n \right)}\left( E \right) $，对于表 E ，重命名为 x ，投影属性重命名为 $ A_1,A_2,...,A_n $

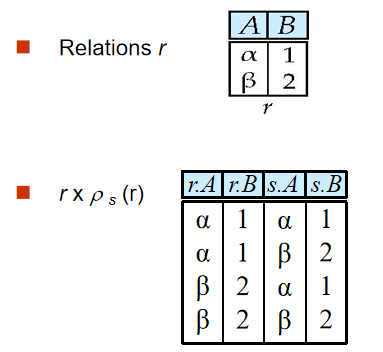
关系代数表达式

  • 定义：把关系或常数关系通过关系代数连接起来形成的表达式

  • 例题：

    • 找出选了教师Einstein所教课程的所有学生的 ID,注意结果不能重复.

      $ \prod\nolimits_{ta.ID}^{}{\left( \sigma _{te.course_id=ta.course_id\land te.\sec tion_id=ta.section_id\land te.semester=ta.semester\land te.year=ta.year}\left( \sigma _{i.ID=te.ID\land name='Eisntein'}\left( \rho _i\left( instructor \right) \times \rho _{te}\left( teaches \right) \times \rho _{ta}\left( takes \right) \right) \right) \right)}$

    • 查出大学里的最高工资

      $ \prod\nolimits_{salary}^{}{\left( instructor \right) -\prod\nolimits_{instructor.salary}^{}{\left( \sigma _{instructor.salary<d.salary}\left( instructor\times \rho _d\left( instructor \right) \right) \right)}}$

附加关系代数（Additional Operations）

1️⃣ 集合交（Set-Intersection Operation）

  • 定义： r $ \cap $ s =

  • 要点：

    • r ，s 必须包含相同属性，即同元
    • r ，s 属性的域必须相容

  • 注意：$ r\cap s=r-\left( r-s \right) $

2️⃣ 除法（Division Operation）

  • 定义：$ r\div s $
  • $ R=\left( A_1,A_2,...A_m,B_1,B_2,...B_n \right) ,S=\left( B_1,B_2,...B_n \right)$
  • 解释：前提是 s 表的属性包含于 r 表。则 r 表属性去掉 s 表的属性之后，r 表中包含 s 表所有数据的元组被选出。其实文字比较难以形容，看图理解更好。

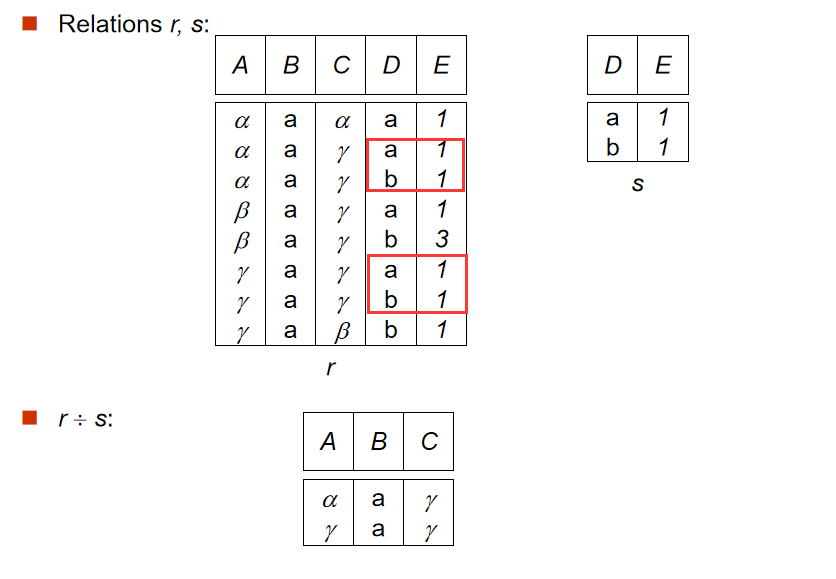
  • 应用：带有“包含某某集合所有元素”的问题，可以使用除法解决

  • 例题：

    • 选出选了计算机系所有课程的学生的 ID：$ \prod\nolimits_{course_id,ID}^{}{\left( takes \right) \div \left( \prod\nolimits_{course_id}^{}{\left( \sigma _{department='Comp.Sci.'}\left( course \right) \right)} \right)}$

3️⃣ 赋值（Assignment Operation）

  • 定义：$ temp\gets expression $，查询结果保存在临时表

4️⃣ 自然连接（Natural Join Operation）

  • 定义：$ r\Join s $，r 表和 s 表根据重复属性进行笛卡尔积，最后去除重复属性

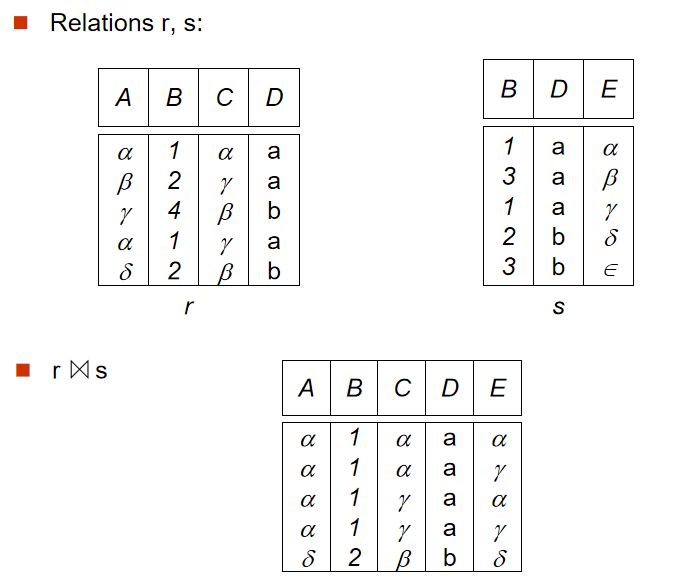
  • 例题：

    • 查找计算机学院所有老师的名字以及他们所上课程的名字

      $ \prod\nolimits_{name,title}^{}{\left( \sigma _{dept_name='Comp.Sci.'}\left( instructor\Join teaches\Join course \right) \right)}$

    • 查找教授 ‘D.B.S' 和 ’O.S‘ 的老师的名字以及课程名称

      $ \prod\nolimits_{name,title}^{}{\left( instructor\Join teaches\Join course \right) } $ \(\div \rho _{title}\left( temp \right) \left( \left\{ \left( ''D.B.S'' \right) ,\left( ''O.S'' \right) \right\} \right)\)

拓展关系代数（Extended Relational-Algebra-Operations）

1️⃣ 广义投影（Generalized Projection）

  • 定义：$ \prod\nolimits_{F_1,F_2,...F_n}^{}{\left( E \right)}$

  • 解释：投影可以进行四则运算

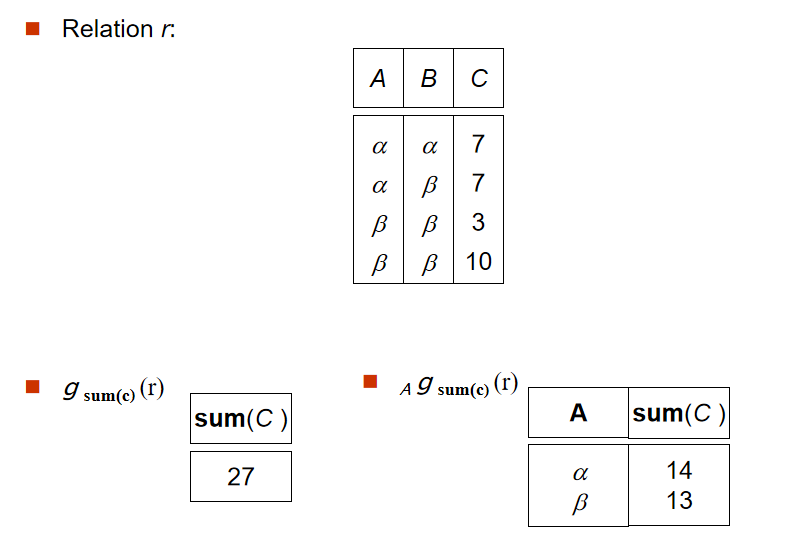
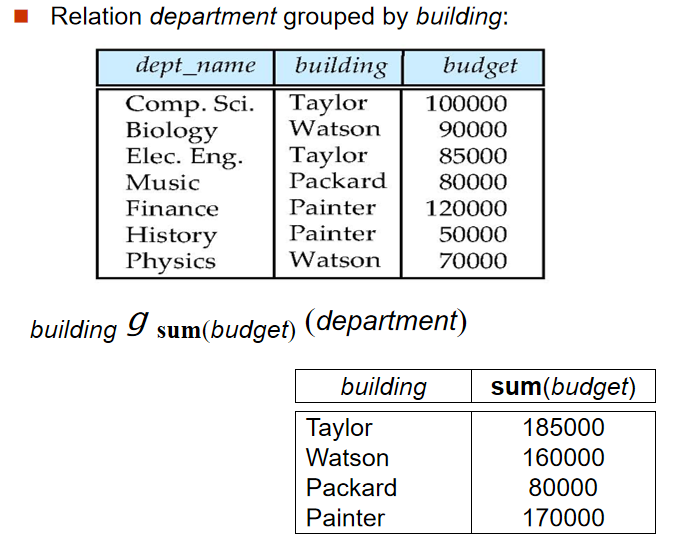
  • 举例：$ \prod\nolimits_{customer,limit-balance}^{}{\left( credit \right)}$

2️⃣ 聚集函数（Aggregate Functions and Operations）

  • 定义：

    \[_{G_1,G_2,...,G_n}g_{F_1\left( A_1 \right) ,F_2\left( A_2 \right) ,...,F_n\left( A_n \right)}\left( E \right) \]

  • 解释：

    • G ：选中进行分组的属性（可以为空）
    • F ：聚集函数（sum，avg ，min ，max ，count）
    • A ：聚集函数作用的属性

  • 要点：

    • 除了 count(*) 会保留 null ，对所有行进行统计，其他聚集函数会忽视值为 null 的属性
    • 可对聚集之后的属性进行更名操作：

      \[_{building}g_{sum\left( budget \right) \,\,as\,\,sum\_budget}\left( department \right) \]

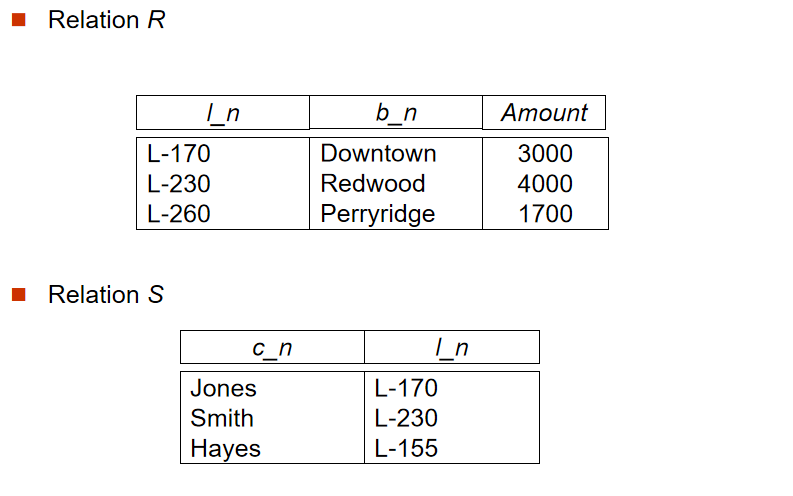
3️⃣ 外连接（Outer Join）

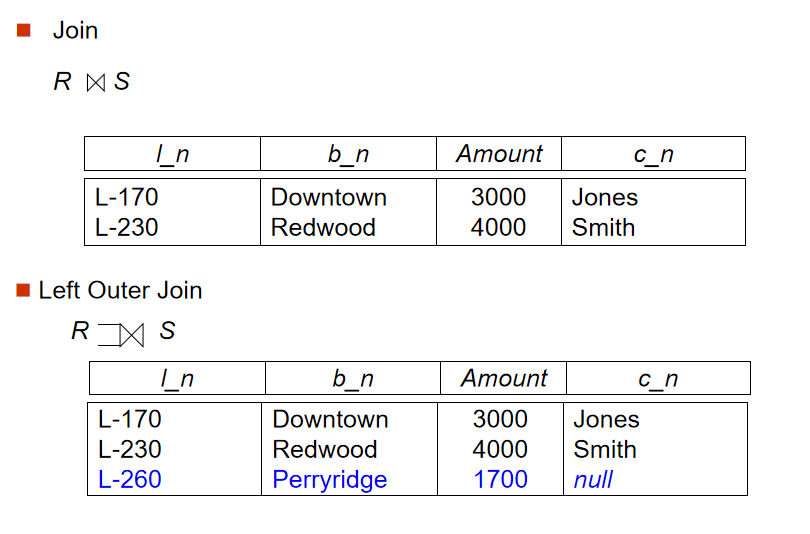
  • 定义：保留连接过程中某表的所有数据，连接操作的延申，能避免信息的丢失

  • 左外连接（左表完整），右外连接（右表完整），全外连接（左右表完整）

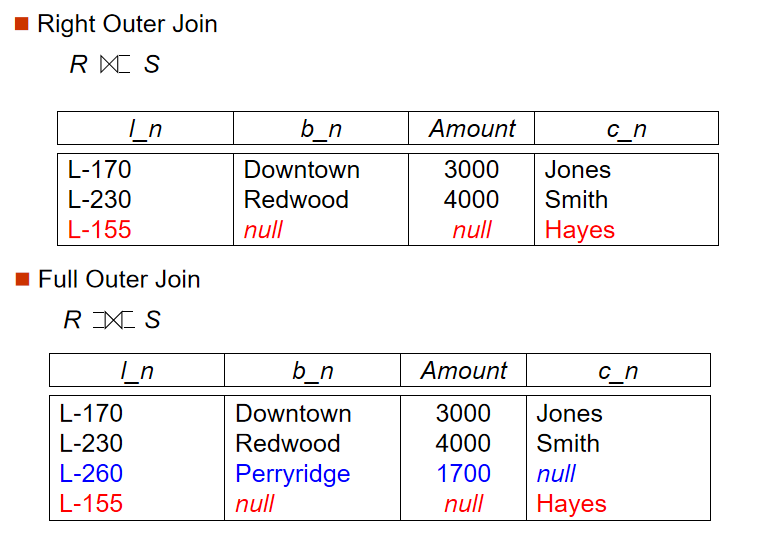
image-20220710221648684image-20220710221658570

NULL值问题

  • 定义：null 表示一个不确定（unknown ）的值，或一个不存在的值

  • unknown 的逻辑运算：优先级上 false < unknown < true

    # OR
unknown or true = true
unknown or false = unknown
unknown or unknown = unknown

# AND
unknown and true = unknown
unknown and false = false
unknown and unknown = unknown 

# NOT
not unknown = unknown

修改关系代数（Modification of the Database）

1️⃣ 删除（Deletion）

  • 定义：$ r\gets r-E $

  • 解释：可以删除整条元组，但不可以删除某些属性

  • 例题：

    • 删除所有物理学院的老师：$ instructor\gets instructor-\sigma _{dept_name='Physics'}\left( instructor \right) $

2️⃣ 插入（Insertion）

  • 定义：$ r\gets r\cup E $

  • 解释：r 表并上查询结果 E ，赋值给 r 表

  • 例题：

    • 插入 instrutor 表，ID 为 1111，教师"Peter"，年薪 72000：

      \[instructor\gets instructor\cup \left\{ \left( ''1111'',''Peter'',,72000 \right) \right\} \]

      \[instructor\gets instructor\cup \left\{ \left( ''1111'',''Peter'',null,72000 \right) \right\} \]

3️⃣ 更新（Updating）

  • 定义：$ r\gets \prod\nolimits_{F_1,F_2,...F_I}^{}{(r)} $

  • 解释：可以改变某个元组当中的某个值。

  • 例题：

    • 所有老师年薪提高百分之五：$ instructor\gets \prod\nolimits_{id,name,dept_name,salary*1.05}^{}{\left( instructor \right)}$

结构化查询语言 SQL

SQL 语言在功能上主要分为如下3大类：

DDL（Data Definition Language、数据定义语言），这些语句定义了不同的数据库、表、视图、索引等数据库对象，还可以用来创建、删除、修改数据库和数据表的结构。主要的语句关键字包括 CREATE 、 DROP 、 ALTER 等。

DML（Data Manipulation Language、数据操作语言），用于添加、删除、更新和查询数据库记录，并检查数据完整性。主要的语句关键字包括 INSERT 、 DELETE 、 UPDATE 、 SELECT 等。SELECT是 SQL 语言的基础，最为重要。

DCL（Data Control Language、数据控制语言），用于定义数据库、表、字段、用户的访问权限和安全级别。主要的语句关键字包括 GRANT 、 REVOKE 、 COMMIT 、 ROLLBACK 、 SAVEPOINT 等

DQL（Data Query Language、数据查询语言)，有时单独把 SELECT 拿出来作为 DQL 分类

DDL（Data Definition Language）

常用数据库数据类型

VARCHAR vs CHAR

CHAR 和 VARCHAR 类型都可以存储比较短的字符串。

  • CHAR 类型
    • CHAR(M) 类型一般需要预先定义字符串长度。如果不指定(M)，则表示长度默认是1个字符。
    • 如果保存时，数据的实际长度比 CHAR 类型声明的长度小，则会在右侧填充空格以达到指定的长度；如果数据的实际长度比 CHAR 类型声明的长度大，则会截取前 M 个字符。当 MySQL 检索 CHAR 类型的数据时，CHAR 类型的字段会去除尾部的空格。
    • 🔔 定义 CHAR 类型字段时，声明的字段长度即为 CHAR 类型字段所占的存储空间的字节数。
    • 🌋 固定长度；浪费存储空间；效率高；适用于存储不大，速度要求高的情况
  • VARCHAR 类型
    • VARCHAR(M) 定义时， 必须指定长度 M，否则报错。
    • MySQL4.0 版本以下，varchar(20)：指的是 20 字节，如果存放 UTF8 汉字时，只能存 6 个（每个汉字 3 字节）；MySQL5.0版本以上，varchar(20)：指的是 20 字符。
    • 🔔 检索 VARCHAR 类型的字段数据时，会保留数据尾部的空格。VARCHAR 类型的字段所占用的存储空间为字符串实际长度加 1 个字节。
    • 🌋 可变长度；节省存储空间；效率低；适合非 CHAR 的情况

CLOB vs BLOB

  • CLOB 类型

    • 将字符大对象 (Character Large Object) 存储为数据库表某一行中的一个列值，使用 CHAR 来保存数据

  • BLOB 类型

    • 可以存储一个二进制的大对象(Binary Large Object)，比如 图片 、音频和视频等

  • 当查询结果是个大对象时，返回的不是对象本身，而是一个定位器

约束

关键词 名称
PIRMARY KEY 主键（唯一+非空）
FOREIGN KEY 外键
UNIQUE 唯一约束
NOT NULL 非空约束
CHECK(p) 谓词约束
INDEX 普通索引 
# PRIMARY KEY
## 创建（1）
CREATE TABLE name(
	ID INT(11) PRIMARY KEY
);
## 创建（2）
CREATE TABLE name(
	ID INT(11),
    PRIMARY KEY(ID)
);
## 创建（3）
ALTER TABLE name ADD PRIMARY KEY(ID);
## 删除
ALTER TABLE name DROP PRIMARY KEY;

# ——————————————————————————————————————————————————————————
# FOREIGN KEY
## 创建（1）
CREATE TABLE name(
	ID INT(11),
    FOREIGN KEY(ID) REFERENCES name2(ID)
);
## 创建（2）
ALTER TABLE name ADD CONSTRAINT fk_name_name1 FOREIGN KEY(ID) REFERENCES name2(ID);
## 删除
ALTER TABLE name DROP FOREIGN KEY fk_name_name1;

# ———————————————————————————————————————————————————————————
# UNIQUE
## 创建（1）
CREATE TABLE name(
	age INT UNIQUE
);
## 创建（2）
CREATE TABLE name(
	age INT,
    UNIQUE KEY(age)
);
## 创建（3）
ALTER TABLE name ADD CONSTRAINT uk_age UNIQUE KEY(age);
## 删除
ALTER TABLE name DROP INDEX uk_age;

# ————————————————————————————————————————————————————————————
# NOT NULL
## 创建（1）
CREATE TABLE name(
	age INT NOT NULL
);
## 创建（2）
ALTER TABLE name CHANGE COLUMN age age INT NOT NULL;
## 删除
ALTER TABLE name CHANGE COLUMN age age INT NULL;

# ————————————————————————————————————————————————————————————
# CHECK(p)
## 创建（1）
CREATE TABLE name(
	num INT CHECK(num > 0)
);
## 创建（2）
ALTER TABLE name ADD CONSTRAINT check_num CHECK(num > 0);
## 删除
ALTER TABLE name DROP CONSTRAINT check_num;

# ————————————————————————————————————————————————————————————
# 创建普通索引 INDEX
## 创建（1）
CREATE TABLE name(
	num INT,
   	INDEX [索引名](num)
);
## 创建（2）
CREATE INDEX 索引名 ON name(num);
## 创建（3）
ALTER TABLE name ADD INDEX 索引名(num);

## 删除索引（1）
ALTER TABLE name DROP INDEX 索引名;
## 删除索引（2）
DROP INDEX 索引名 ON name;

用户自定义数据类型（User-Defined Types）

  • 用户对已有数据类型的特指和更名

  • MySQL 不支持

    CREATE type 类型名 as 类型
# 例如：create type Dollars as numeric (12,2) final

  • 强类型检查，只要自定义类型名字不同，数据类型就不同

域（Domains）

  • 本质是可以带约束的用户自定义数据类型

  • MySQL 不支持

    create domain 域名 类型 限制
# 例如：create domain person_name char(20) not null

DQL（Data Query Language）

SELECT [DISTINCT]FIELD1,FIELD2...
FROM TRABLE1[,TABLE2...]
[INNER]JOIN | LEFT [OUTER] JOIN | RIGHT [OUTER] JOIN | NATURAL JOIN TABLE3
ON 关联条件... | USING(FIELD1,FIELD2...)
WHERE 查询条件或子查询
GROUP BY FIELD1,FIELD2...
HAVING 分组条件
ORDER BY FIELD1,FIELD2... [ASC][DESC]
UNION [ALL] 并上其他表的查询结果

  • SELECT ：查询。

  • From ：指明查询的表，可以是实际存在的表，也可以是查询产生的临时表。

  • DISTINCT ：对数据表中一个或多个字段重复的数据进行过滤，只返回其中的一条数据给用户，删除重复数据。

  • [INNER]JOIN 内连接，LEFT [OUTER] JOIN 左外连接，LEFT [OUTER] JOIN 右外连接，NATURAL JOIN 自然连接，注意 MySQL 不支持全表连接 FULL JOIN 但是可以通过 LEFT JOIN UNION RIGHT JOIN 实现。

  • WHERE ：指明查询条件，可以没有。

  • GROUP BY ：分组

  • HAVING ：分组后对每个组进行筛选，可以使用聚集函数（avg,sum...）

  • ORDER BY ：查询结果排序，ASC 升序，DESC 降序

  • UNION [ALL] ：合并多表查询结果，默认去重，加 ALL 不去重

HAVING vs WHERE

  • HAVING ：谓词在分组后应用
  • WHERE ：谓词在分组前应用

SOME vs ALL

  • SOME ：满足一个条件即为真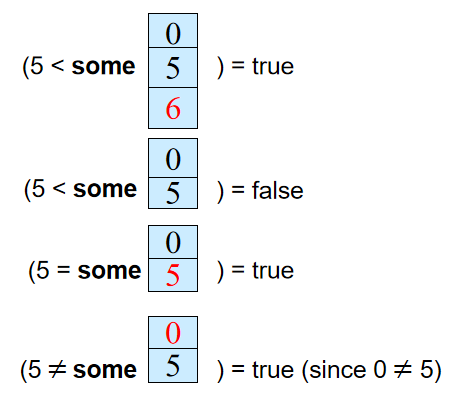

    输出所有比生物系某些老师工资高的老师的姓名。

    select name
from instructor
where salary > SOME (
    select salary
    from instructor
    where dept name = ’Biology’
);

  • ALL ：满足所有条件为真

    输出比生物学院所有教师工资都高的教师的名字。

    select name
from instructor
where salary > ALL (
    select salary
    from instructor
    where dept name = ’Biology’
);

EXISTS vs NOT EXISTS

  • EXISTS ：如果在子查询中不存在满足条件的行，返回 false ；如果在子查询中存在满足条件的行，返回 true

    Exists 执行的流程 Exists 首先执行外层查询，再执行内存查询。流程为首先取出外层中的第一元组，再执行内层查询，将外层表的第一元组代入，若内层查询为真，即有结果时。返回外层表中的第一元组，接着取出第二元组，执行相同的算法。一直到扫描完外层整表

    例题：找出所有在 2018 年秋季并且在 2019 年春季开课的课程

     select course_id   
 from section as S   
 where semester = ’Fall’ and year = 2009 and exists (
     select *  from section as T                            
     where semester = ’Spring’ and year= 2010 and S.course_id = T.course_id
 );

  • NOT EXISTS ：如果在子查询中不存在满足条件的行，返回 true；如果在子查询中存在满足条件的行，返回 false。可以用于处理关系代数中的除法

    例题：查询选了计算机学院开设的所有课程的学生的姓名。

    SELECT student.`name` 
FROM student 
WHERE NOT EXISTS ( 
    SELECT * FROM course 
    WHERE course.dept_name = "Comp. Sci." AND NOT EXISTS ( 
        SELECT * FROM takes 
        WHERE takes.ID = student.ID AND takes.course_id = course.course_id 
    ) 
);

    内部循环：查询出该生没有选择的所有的计算机学院课程

     SELECT * FROM course 
    WHERE course.dept_name = "Comp. Sci." AND NOT EXISTS ( 
        SELECT * FROM takes 
        WHERE takes.ID = student.ID AND takes.course_id = course.course_id 
    )

    外部循环：查询不存在没有选择计算机学院所有课程的学生姓名 = 查询选了计算机学院开设的所有课程的学生的姓名。如果该生没有选择的所有的计算机学院课程 NOT EXISTS 则为 true，输出。

WITH查询

  • 定义：创建一个只能查询的临时表

  • 用法：

    WITH TABLE_NAME[(FIEDL1,FIELD2...)] AS (查询语句)

  • 例题：查询平均年薪大于所有部门总平均的部门

    with dept _total (dept_name, value) as (
         select dept_name, sum(salary)
         from instructor
         group by dept_name
	 ),
	 dept_total_avg(value) as (
       select avg(value)
       from dept_total
     )
select dept_name
from dept_total, dept_total_avg
where dept_total.value > dept_total_avg.value;

  • WITH 查询可以实现递归查询

    🌰例子 ：查询每个课程的所有前驱课程

    WITH recursive rec_prereq ( course_id, prereq_id ) AS (
	SELECT course_id, prereq_id 
	FROM prereq 
	UNION
	SELECT rec_prereq.course_id, prereq.prereq_id
	FROM rec_prereq, prereq 
	WHERE
		rec_prereq.prereq_id = prereq.course_id
	) 
SELECT * FROM rec_prereq

DML（Data Manipulation Language）

1️⃣ 增（Insertion）

# 对表中所有字段都添加值
INSERT INTO TABLE_NAME VALUES(VALUE1,VALUE2,...);

# 对表中指定字段添加值
INSERT INTO TABLE_NAME(FIELD1,FIELD2,...) VALUES(VALUE1,VALUE2,...);

# 
INSERT INTO TABLE_NAME SELECT ... FROM

2️⃣ 删（Deletion）

DELETE FROM TABLE_NAME [WHERE 条件]

3️⃣ 改（Updates）

UPDATE FIELD1 SET FIELD1 = ... [WHERE ...]
  • 注意语句顺序问题
 update instructor set salary = salary * 1.03 where salary > 100000;
 update instructor set salary = salary * 1.05 where salary <= 100000;
 # 顺序不可颠倒

可修改为使用 CASE

update instructor set salary = 
	case 
        when salary <= 100000 then salary * 1.05 
        else salary * 1.03
    end;

DCL(Data Control Language)

  • 用户管理

1️⃣ 创建用户

CREATE USER 用户名[@ 主机名] [IDENTIFIED BY '密码']
# 例子：CREATE USER 'user'@'localhost' IDENTIFIED BY '123456';

2️⃣ 查询用户信息

SELECT * FROM mysql.user;
SELECT Host,User,authentication_string from mysql.user

3️⃣ 修改用户

UPDATE mysql.user SET USER='li4' WHERE USER='wang5'; 
FLUSH PRIVILEGES; # 刷新数据库

4️⃣ 删除用户

DROP USER 用户名[@主机名] ;# 默认删除host为%的用户
# 例子：DROP USER 'tom';
  • 权限管理

1️⃣ 授予权限

GRANT 权限1,权限2,…权限n ON 数据库名称.表名称 TO 用户名@用户地址 [IDENTIFIED BY ‘密码口令’];

# 例子：
# 给用户‘aaa’@‘%’赋予所数据库所有表的读的权限，但是它没有权利给别人赋权；
grant select on *.* to 'aaa' @ '%';
# 给用户‘aaa’@‘%’赋予所数据库所有表的读的权限，也有权利给别人赋权；
grant select on *.* to 'aaa' @ '%' with grant option

权限：

  • SELECT
  • UPDATE
  • DELETE
  • INSERT
  • ALL PRIVILEGES ：代替所有权限

2️⃣ 收回权限

REVOKE 权限1,权限2,…权限n ON 数据库名称.表名称 FROM 用户名@用户地址;

#收回全库全表的所有权限 
REVOKE ALL PRIVILEGES ON *.* FROM joe@'%'; 
#收回mysql库下的所有表的插删改查权限 
REVOKE SELECT,INSERT,UPDATE,DELETE ON mysql.* FROM joe@localhost;
  • 须用户重新登录后才能生效

视图（View）

  • 定义：

    • 视图是一种 虚拟表 ，本身是 不具有数据 的，占用很少的内存空间，它是 SQL 中的一个重要概念。
    • 视图建立在已有表的基础上, 视图赖以建立的这些表称为基表。
    • 视图的创建和删除只影响视图本身，不影响对应的基表。但是当对视图中的数据进行增加、删除和修改操作时，数据表中的数据会相应地发生变化，反之亦然。
    • 向视图提供数据内容的语句为 SELECT 语句, 可以将视图理解为存储起来的 SELECT 语句
    • 视图不会保存数据，数据真正保存在数据表中。当对视图中的数据进行增加、删除和修改操作时，数据表中的数据会相应地发生变化；反之亦然。
    • 不建议对视图进行修改，一般只用于查询

  • 优点：

    • 操作简单：将经常使用的查询操作定义为视图，可以使开发人员不需要关心视图对应的数据表的结构、表与表之间的关联关系，也不需要关心数据表之间的业务逻辑和查询条件，而只需要简单地操作视图即可，极大简化了开发人员对数据库的操作。

    • 减少数据冗余：视图跟实际数据表不一样，它存储的是查询语句。所以，在使用的时候，我们要通过定义视图的查询语句来获取结果集。而视图本身不存储数据，不占用数据存储的资源，减少了数据冗余。

    • 数据安全：MySQL将用户对数据的 访问限制 在某些数据的结果集上，而这些数据的结果集可以使用视图来实现。用户不必直接查询或操作数据表。这也可以理解为视图具有 隔离性 。视图相当于在用户和实际的数据表之间加了一层虚拟表。同时，MySQL可以根据权限将用户对数据的访问限制在某些视图上，用户不需要查询数据表，可以直接通过视图获取数据表中的信息。这在一定程度上保障了数据表中数据的安全性。

    • 适应灵活多变的需求 当业务系统的需求发生变化后，如果需要改动数据表的结构，则工作量相对较大，可以使用视图来减少改动的工作量。这种方式在实际工作中使用得比较多。

    • 能够分解复杂的查询逻辑 数据库中如果存在复杂的查询逻辑，则可以将问题进行分解，创建多个视图获取数据，再将创建的多个视图结合起来，完成复杂的查询逻辑。

  • 不足：

    • 难以维护：如果实际数据表的结构变更了，我们就需要及时对相关的视图进行相应的维护.特别是嵌套的视图（就是在视图的基础上创建视图），维护会变得比较复杂， 可读性不好 ，容易变成系统的潜在隐患。因为创建视图的 SQL 查询可能会对字段重命名，也可能包含复杂的逻辑，这些都会增加维护的成本。

      实际项目中，如果视图过多，会导致数据库维护成本的问题。

  • 用法

    # 创建视图
CREATE VIEW 视图名称 AS (查询语句)

# 详细版
CREATE [OR REPLACE] 
[ALGORITHM = {UNDEFINED | MERGE | TEMPTABLE}] 
VIEW 视图名称 [(字段列表)] 
AS 查询语句 
[WITH [CASCADED|LOCAL] CHECK OPTION]

# 增删改查操作将视图看作普通表即可

# 可以基于视图创建视图

# 修改视图
ALTER VIEW 视图名称 AS 查询语句

# 删除视图
DROP VIEW IF EXISTS 视图名称;

  • 不可更新视图

    • 在定义视图的时候指定了“ALGORITHM = TEMPTABLE”，视图将不支持 INSERT 和 DELETE 操作；
    • 视图中不包含基表中所有被定义为非空又未指定默认值的列，视图将不支持 INSERT 操作；
    • 在定义视图的 SELECT 语句中使用了 JOIN 联合查询 ，视图将不支持 INSERT 和 DELETE 操作；
    • 在定义视图的 SELECT 语句后的字段列表中使用了 数学表达式 或 子查询 ，视图将不支持 INSERT ，也不支持 UPDATE 使用了数学表达式、子查询的字段值；
    • 在定义视图的 SELECT 语句后的字段列表中使用 DISTINCT 、 聚合函数 、 GROUP BY 、 HAVING 、 UNION 等，视图将不支持 INSERT 、UPDATE、DELETE；
    • 在定义视图的 SELECT 语句中包含了子查询，而子查询中引用了 FROM 后面的表，视图将不支持 INSERT、UPDATE、DELETE；
    • 视图定义基于一个不可更新视图 ；
    • 常量视图。

存储过程（Stored Procedure）

  • 定义：

    • 存储过程是一组经过预先编译 的 SQL 语句的封装。预先存储在 MySQL 服务器上，需要执行的时候，客户端只需要向服务器端发出调用存储过程的命令，服务器端就可以把预先存储好的这一系列 SQL 语句全部执行。
    • 直接操作数据库底层数据结构，一般用于进行更复杂的数据处理
    • 没有返回值
    • 参数类型：
      • IN ：当前参数为输入参数，也就是表示入参；默认为 IN。
      • OUT ：当前参数为输出参数，也就是表示出参。
      • INOUT ：当前参数既可以为输入参数，也可以为输出参数。
    • 存储过程的功能更加强大，包括能够执行对表的操作（比如创建表，删除表等）和事务操作，这些功能是存储函数不具备的。

  • 用法

    # 创建存储过程
CREATE PROCEDURE 存储过程名(IN|OUT|INOUT 参数名 参数类型,...) 
[characteristics ...] 
BEGIN
存储过程体 
END

# 删除存储过程
DROP PROCEDURE 存储过程名 [IF EXISTS];

  • 举例

    DELIMITER // 
CREATE PROCEDURE show_someone_salary2(IN empname VARCHAR(20),OUT empsalary DOUBLE) 
    BEGIN
   		SELECT salary INTO empsalary FROM emps WHERE ename = empname; 
    END // 
DELIMITER ;

    DELIMITER // 
CREATE PROCEDURE show_mgr_name(INOUT empname VARCHAR(20)) 
    BEGIN
    	SELECT ename INTO empname FROM emps WHERE eid = (SELECT MID FROM emps WHERE ename=empname); 
    END // 
DELIMITER ;

  • 调用存储过程

    # 调用in模式的参数
CALL 存储过程名(实参列表)

# 调用out模式的参数
SET @name; 
CALL sp1(@name); 
SELECT @name;

# 调用inout模式的参数
SET @name=value; 
CALL sp1(@name); 
SELECT @name;

# 例 1
DELIMITER // 
CREATE PROCEDURE CountProc(IN sid INT,OUT num INT) 
    BEGIN
    	SELECT COUNT(*) INTO num FROM fruits WHERE s_id = sid; 
    END // 
DELIMITER ;

SET @name;
CALL CountProc (101, @num);
SELECT @name;

# 例 2
DELIMITER // 
CREATE PROCEDURE `add_num`(IN n INT) 
    BEGIN 
        DECLARE i INT; 
        DECLARE sum INT;
        SET i = 1; 
        SET sum = 0; 
        WHILE i <= n DO 
        	SET sum = sum + i; 
        	SET i = i +1; 
        END WHILE; 
        SELECT sum; 
    END // 
DELIMITER ;

CALL add_num(50);

  • 优点

    • 存储过程可以一次编译多次使用。存储过程只在创建时进行编译，之后的使用都不需要重新编译，这就提升了 SQL 的执行效率。

    • 可以减少开发工作量。将代码 封装 成模块，实际上是编程的核心思想之一，这样可以把复杂的问题拆解成不同的模块，然后模块之间可以 重复使用 ，在减少开发工作量的同时，还能保证代码的结构清晰。

    • 存储过程的安全性强。我们在设定存储过程的时候可以设置对用户的使用权限 ，这样就和视图一样具有较强的安全性。

    • 可以减少网络传输量。因为代码封装到存储过程中，每次使用只需要调用存储过程即可，这样就减少了网络传输量。

    • 良好的封装性。在进行相对复杂的数据库操作时，原本需要使用一条一条的 SQL 语句，可能要连接多次数据库才能完成的操作，现在变成了一次存储过程，只需要 连接一次即可 。

  • 缺点：

    • 可移植性差。存储过程不能跨数据库移植，比如在 MySQL、Oracle 和 SQL Server 里编写的存储过程，在换成其他数据库时都需要重新编写。

    • 调试困难。只有少数 DBMS 支持存储过程的调试。对于复杂的存储过程来说，开发和维护都不容易。虽然也有一些第三方工具可以对存储过程进行调试，但要收费。

    • 存储过程的版本管理很困难。比如数据表索引发生变化了，可能会导致存储过程失效。我们在开发软件的时候往往需要进行版本管理，但是存储过程本身没有版本控制，版本迭代更新的时候很麻烦。

    • 它不适合高并发的场景。高并发的场景需要减少数据库的压力，有时数据库会采用分库分表的方式，而且对可扩展性要求很高，在这种情况下，存储过程会变得难以维护， 增加数据库的压力 ，显然就不适用了。

阿里开发规范

【强制】禁止使用存储过程，存储过程难以调试和扩展，更没有移植性。

函数（Function）

  • 定义：

    • MySQL 支持自定义函数，定义好之后，调用方式与调用 MySQL 预定义的系统函数一样。
    • 有返回值
    • 用户自己定义的存储函数与MySQL内部函数是一个性质的。区别在于，存储函数是 用户自己定义 的，而内部函数是 MySQL 的开发者定义的。
    • 参数类型：总是默认为 IN 参数。
    • RETURNS 子句只能对 FUNCTION 做指定，对函数而言这是强制的。它用来指定函数的返回类型，而且函数体必须包含一个 RETURN value 语句。
    • 存储函数可以放在查询语句中使用，存储过程不行

  • 用法

    # 创建函数
CREATE FUNCTION 函数名(参数名 参数类型,...) 
RETURNS 返回值类型 
[characteristics ...] 
BEGIN
	函数体 #函数体中肯定有 RETURN 语句 
END

# 删除函数
DROP FUNCTION 函数名 [IF EXISTS]

  • 调用函数

    SELECT 函数名(实参列表)

  • 举例

    DELIMITER // 
CREATE FUNCTION count_by_id(dept_id INT) 
RETURNS INT 
    LANGUAGE SQL 
    NOT DETERMINISTIC 
    READS SQL DATA SQL 
    SECURITY DEFINER 
    COMMENT '查询部门平均工资' 
BEGIN
	RETURN (SELECT COUNT(*) FROM employees WHERE department_id = dept_id); 
END //
DELIMITER ;

SET @dept_id = 50; 
SELECT count_by_id(@dept_id);

实体联系模型（Entity-Relationship Model）

建模（Modeling）

ER 模型中的三个基本概念

  • 实体集（Entity Sets）

    • 实体：是一个存在的物体，且区别于其他物体。实体可以表示为一组属性的集合

    • 实体集：是具有相同类型，共享相同属性的实体的集合。

    • 一个或一些属性形成主键（pirmary key）可唯一区分实体集中的每一个实体

    • 强实体集（Strong Entity Sets）：有主码的实体集，通过主码区分每一个实体

    • 弱实体集（Weak Entity Sets）：没有足够的属性以形成主码的实体集

      • 每个弱实体集必须与一个标识实体集（强实体集）建立联系。

      • 与弱实体集建立联系的联系集叫做标识性联系（Identifying Relationship）。

      • 虽然弱实体集没有主码，但是我们仍需要区分依赖于特定强实体集的弱实体集中的实体的方法。弱实体集的分辨符（discriminator）是使得我们进行这种区分的属性集合。

      • 弱实体集的主码由标识实体集的主码加上该弱实体集的分辨符构成。

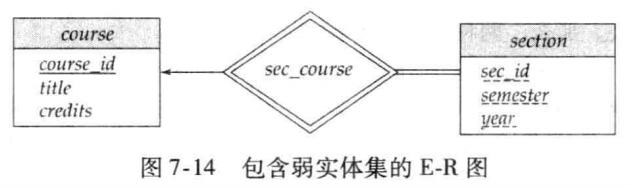
        🌰 图 7-14 中弱实体集 section 的主码由 course_id，sec_id，semester，year 组成。其中 course_id 是 course 的主码，sec_id，semester，year 是 section 的分辨符，用于区分每个 course 的不同 section。

  • 联系集（Relationship Sets）

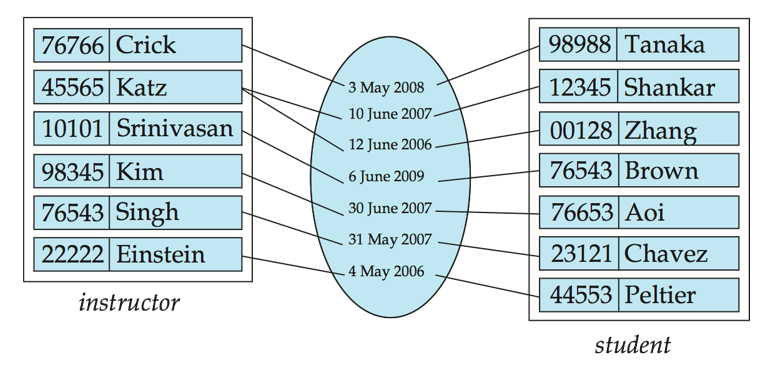
    \[\left\{ \left( e_1,e_2,...e_n \right) |e_1\in E_1,e_2\in E_2,...,e_n\in E_n \right\} \]

    • 连接两个或多个实体
    • 联系集也可以有属性
    • 联系集的度（Degree of a Relationship Set）：即连接实体集的个数，多数情况联系集是二元联系（binary relationship），很少有多元联系。

  • 属性（Attributes）

    • 单值和多值属性（Single-valued and multivalued Attributes）：例如，人有多个电话号码，是多值

    • 简单和复合属性（Simple and composite Attributes）：例如，英文名可拆分为 first name ，last name ，是复合属性

    • 派生属性（Derived Attributes）：可以从其他别的属性或实体派生出来。例如：年龄（根据出生日期和当前日期计算得出）

    • 冗余属性（Redundant Attributes）

    • 域（Domain）：每个属性的取值范围

映射基数约束（Mapping Cardinality Constraints）

  • 定义：表示一个实体通过一个联系集能够关联的实体的个数

  • 对于二元关系集，映射基数包含如下四种类型

    • 一对一（One to one）

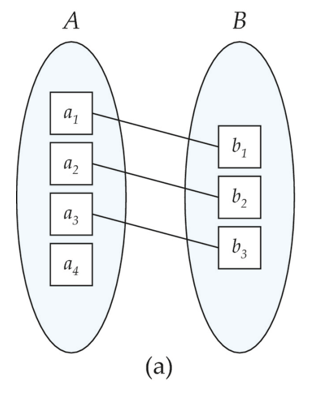
    • 一对多（One to many）

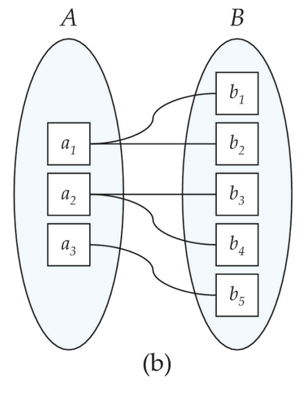
    • 多对一（Many to one）

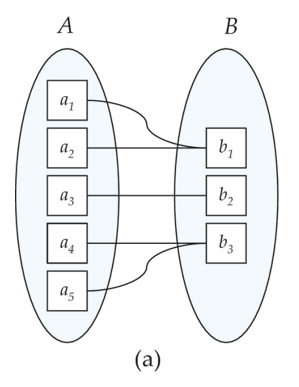
    • 多对多（Many to many）

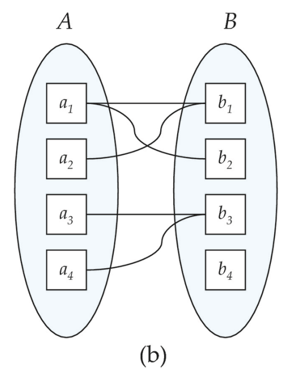
实体-联系图（E-R Diagrams）

1️⃣ 实体：矩形表示实体，属性写矩形内部，下划线表示主码

2️⃣ 联系：菱形表示联系（联系可以有属性）

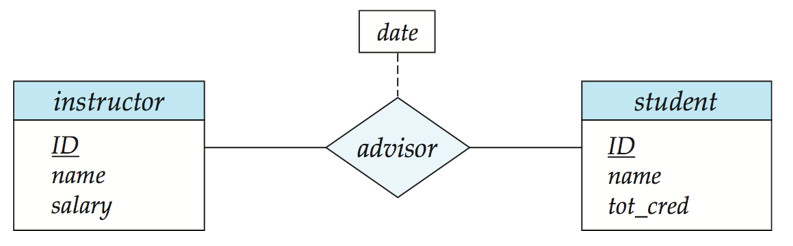
3️⃣ 连线：只能连接实体和属性、实体和联系，不能连接实体和实体或联系和联系

4️⃣ 属性：

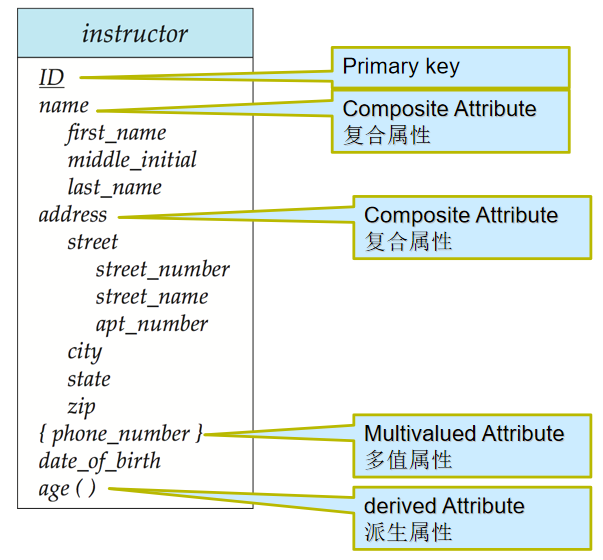
5️⃣ 角色（Roles）：实体在联系中扮演的功能叫做实体的角色。当相同实体集在联系中扮演不同的角色的时候（自连接），需显示标记角色信息

6️⃣ 基数约束（Cardinality Constraints）：

  • 联系集指向实体集
  • 有向连线➡️表示一个（One）
  • 无向连线➖表示多个（Many）

一个 instructor 通过 advisor 与若干（包括 0）student 联系（0..*）

一个 student 通过 advisor 与最多一个 instructor 联系（1..1）

  • 表达更复杂的映射基数约束

    • l..h ：l 表示基数最小值，h 表示基数最大值

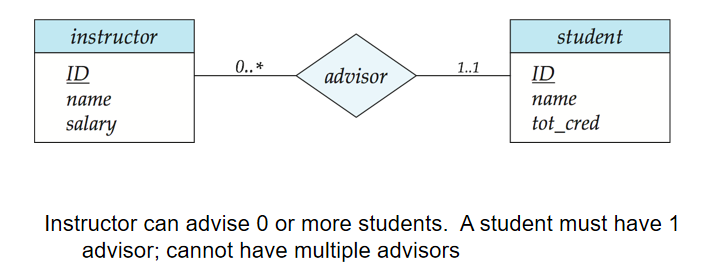
7️⃣ 全参与和部分参与（Total and Partial Participation）

  • 全参与：每个实体至少参与了联系集中的某一个联系（双线）
  • 部分参与：某些实体可能未参与联系集中的任何一个联系（单线）

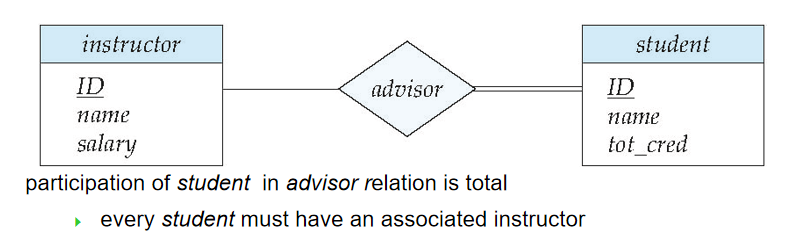
8️⃣ 弱实体集（Weak Entity Sets）

  • 弱实体集表示为双层矩形
  • 弱实体集的分辨符用虚下划线标出
  • 弱实体集和标志性强实体集间的联系集用双层菱形表示。
  • 弱实体集与标识实体集之间必然是多对一关系，且弱实体集的实体全部参与

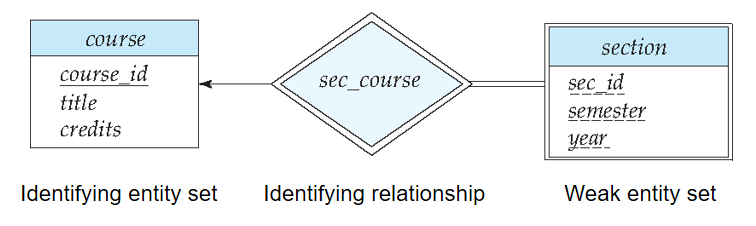
转化为关系模式（Reduction to Relation Schemas）

  • 实体集和联系集都可以转化为关系模式，用以存储数据库中的内容
  • 若数据库符合 E-R 图，则可以表示成模式的集合
  • 在 E-R 图中，每个实体集和联系集均对应一个唯一的模式
  • 在每个模式中，均有多个列，且模式内列名不重复。

1️⃣ 强实体集使用相同属性转化成关系模式

🌰 例如

强实体集：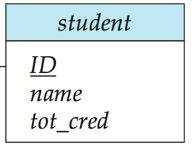

关系模式：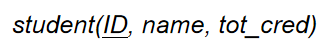

2️⃣ 弱实体集包含标志性强实体集中的主码。

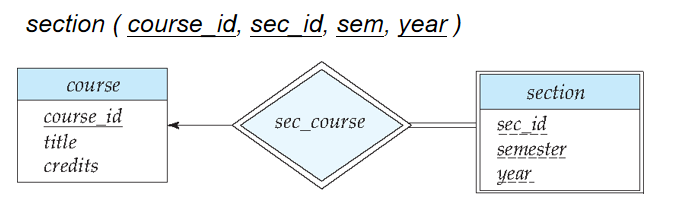
3️⃣ 对于联系集：

  1. 多对多的联系集也应表示成关系模式，其属性包含参与该联系的实体集的主码的并集和它自身的描述属性。

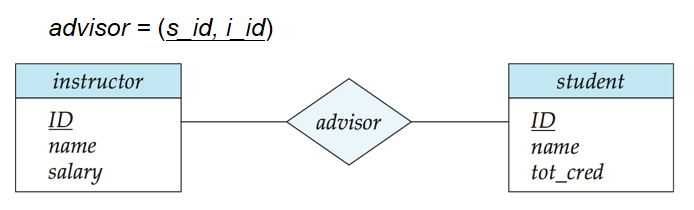
同一实体集内部多对多：

  1. 多对一或一对多的联系集不转化为关系模式，而是将多（Many）的一端的实体集中加入一（One）那一端的实体集的主码。

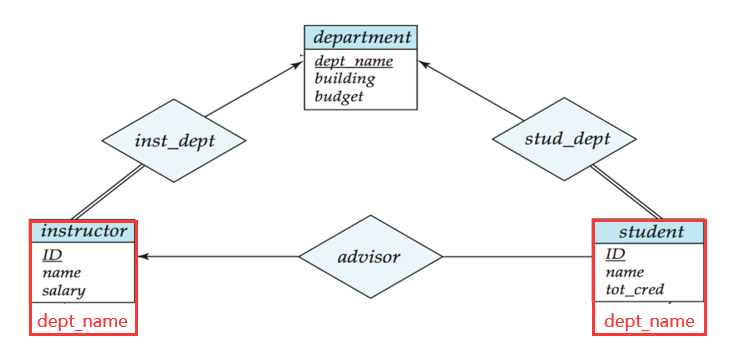
自引用（同一实体集内部不同实体之间多对一）：

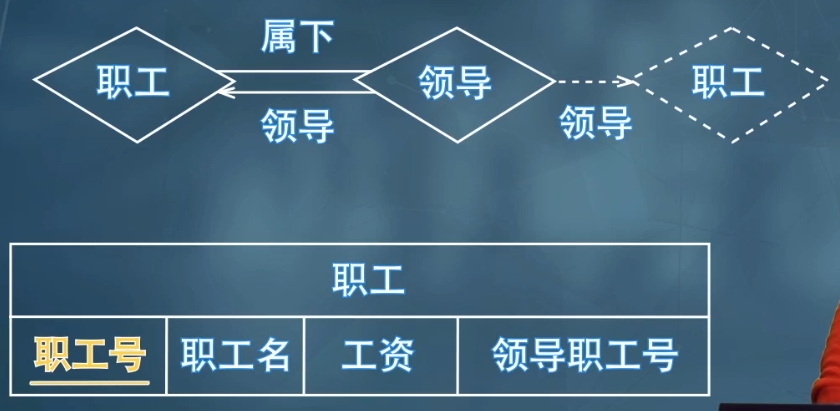
  1. 一对一的关系集可将任意一端看作多的那一端。如果多的那一端的实体集是部分参与的，转化成关系模式之后，有些元组的属性中会出现 NULL。
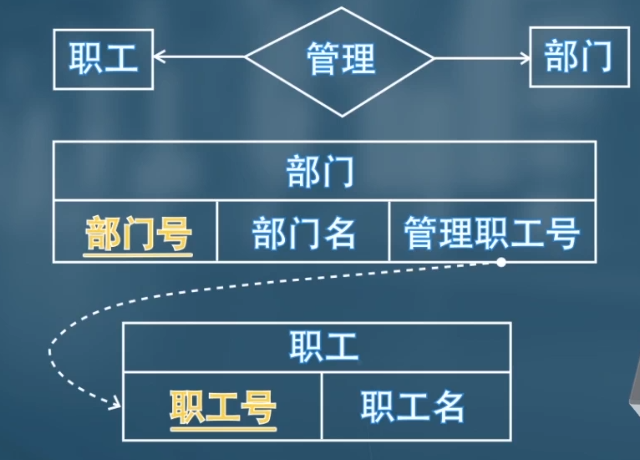
  1. 一般情况下，连接弱实体集与其所依赖的强实体集的联系集的模式是冗余的，而且在基于 E-R 图的关系数据库设计中不必给出。实体集当成多对一处理即可。

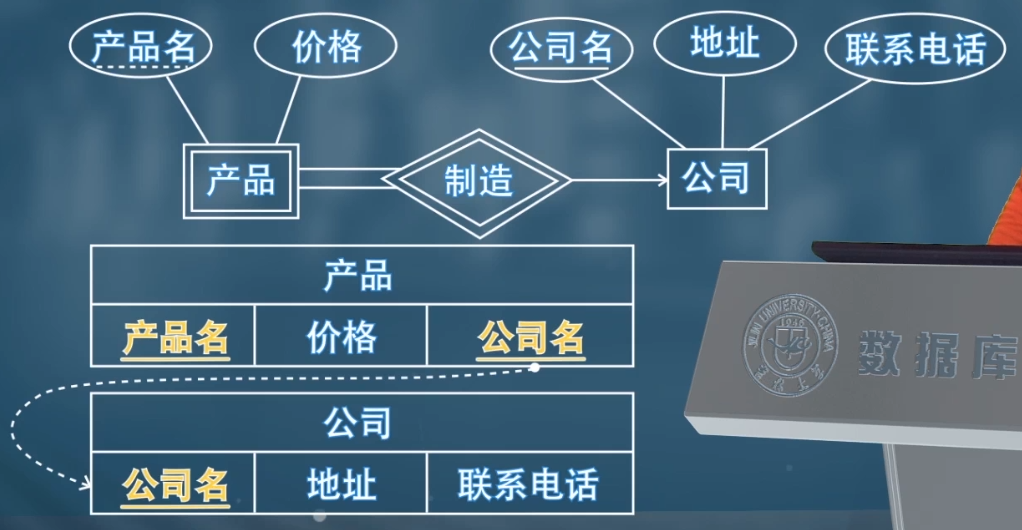
4️⃣ 对于属性：

  1. 复合属性忽视所有父级属性，将子属性创建单独的属性
  2. 忽视多值属性，将多值属性表示成一个单独的模式 EM（原实体集 E，多值属性 M）。多值属性的每一个取值都会映射成为这个新的模式内的一条元组
  3. 忽视派生属性

5️⃣ 对于特化

  1. 低层实体转化成模式的时候，只包含高层模式的主码和自己独有属性

    缺点：获取低层实体继承的属性时需要访问高层实体。

  2. 每个实体集对应的模式中记录所有的属性，包括局部和继承的属性。

    缺点：数据冗余

​

6️⃣ 对于聚集：

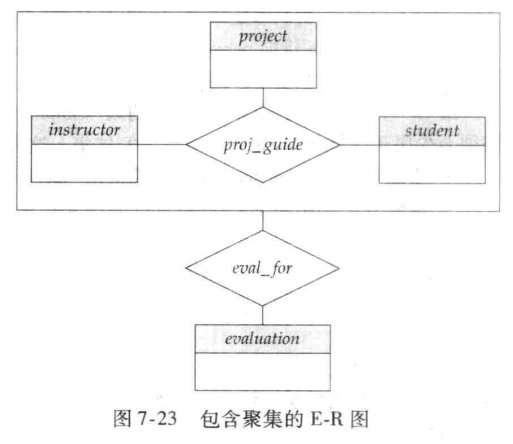
表示聚集和实体集之间联系的联系集（eval_for）需要包含：

  • 聚集联系的主码（i_ID，s_ID，project_ID）

  • 关联实体集的主码（evaluation_ID）

  • 联系集的描述属性

实体-联系设计问题（Design Issues）

1. 用实体集还是用属性

没有一个固定的说法，需要依据企业实际情况进行设计。

定义为实体集可以添加更多的拓展信息，但会造成查询时损失效率。

定义为属性可以提高查询速度，方便查询，但会造成信息缺失，拓展性差。

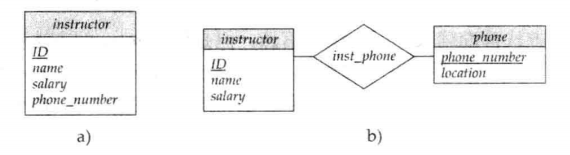
🔔 有两个常犯的错误：

1️⃣ 用一个实体集的主码作为另一个实体集的属性,而不是用联系。例如，即时每名教师只指导一名学生，将 student 的 ID 作为 instructor 的属性也是不正确的。用 advisor 联系代表学生和教师之间的关联才是正确的方法，因为这样可以明确地表示出两者之间的关系而不是将这种关系隐含在属性中。

2️⃣ 将相关实体集的主码属性作为联系集的属性。例如，ID ( student 的主码属性) 和 ID( instructor 的主码)不应该在 advisor 联系中作为属性出现。这样做是不对的，因为在联系集中已经隐含了这些主码属性。

2. 用实体集还是用联系集

原则：当描述发生在实体间的行为时采用联系集。

有的时候用实体集实体集还是联系集都可以，这个时候推荐根据原则进行重新考虑。

有的时候则只能使用实体集或联系集。

🌰 例如：购物系统，用户只能通过代理购买商品，定义三个实体集 customer ，production，Agent

下面考虑用实体集还是联系集将三个实体集联系起来，如果使用联系集 order

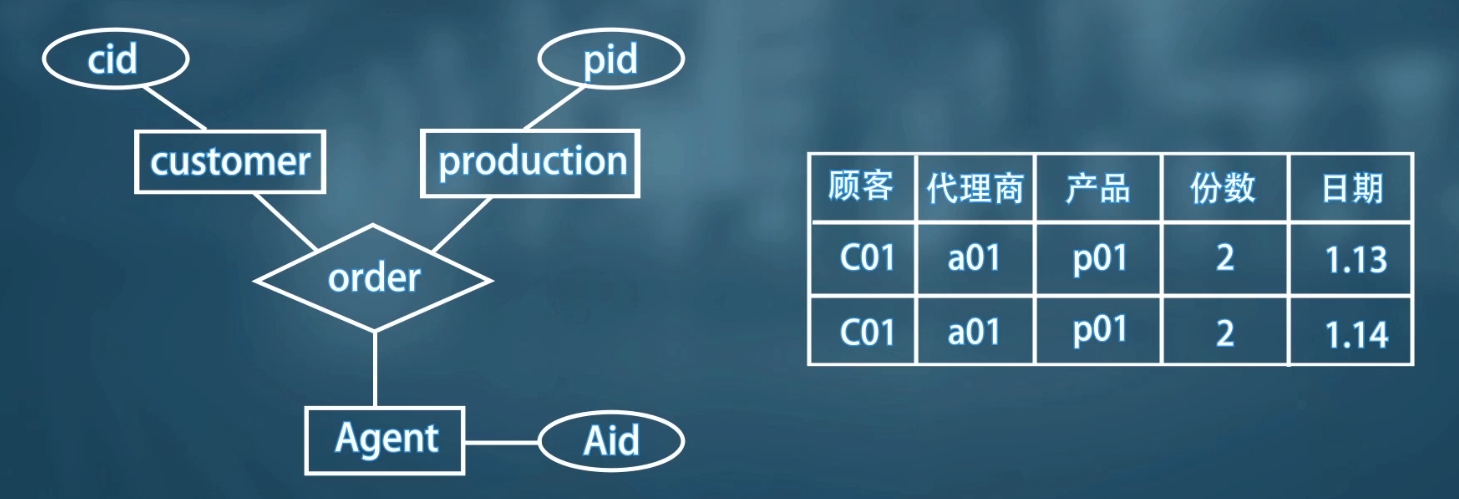
根据 E-R 图的定义，多对多时，联系集转化成关系时主键由所有与其联系的实体集的主键组成（顾客、代理商、产品），联系集可以有自己的属性（份数，日期）。这是发现，无法通过 order 的主键唯一区分一条记录。

应该使用实体集。

3. 二元还是 n 元联系集

数据库通常是二元联系，但有的联系用 n 元联系集表示更清晰。

一个 n（n > 2） 元联系总可以用一组二元联系代替。

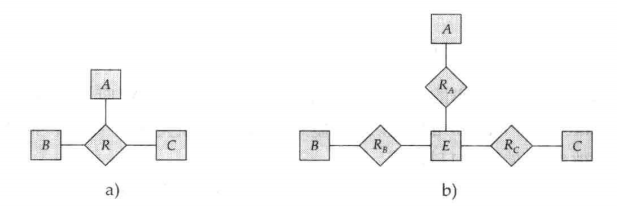
a）：R（a，b，c）

b）：E（e，a，b，c），RA（e，a），RB（e，b），RC（e，c）

一些限制：

  • 对于为表示联系集而创建的实体集，我们可能不得不为其创建一个标识属性。该标识属性和额外所需的那些联系集增加了设计的复杂程度以及对总的存储空间的需求
  • n 元联系集可以更清晰地表示几个实体集参与单个联系集。
  • 有可能无法将三元联系上的约束转变为二元联系上的约束。例如，考虑一个约束，表明 R 是从A、B 到 C 多对一的;也就是，来自 A 和 B 的每一对实体最多与一个 C 实体关联。这种约束就不能用联系集 RA、RB 和 RC 上的基数约束来表示。

4. 联系集的属性布局

考虑联系集中放置什么属性。

一对一联系集的属性可以放到任意一个与其联系的实体集中。

一对多或多对一联系集的属性可以放到“多方”的实体集中.

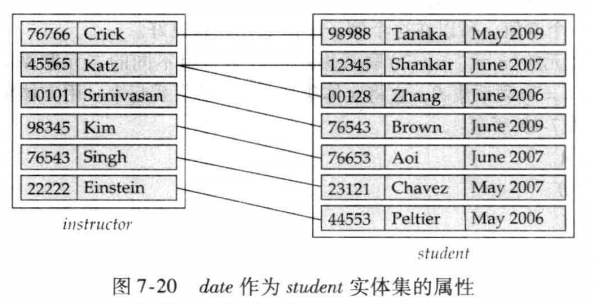
🌰 例如：student 和 instructor 通过 advisor 建立多对一联系，联系集 advisor 中有 date 属性记录学生选择导师的时间，该属性可以放在 student 实体集中，等价于放在联系集中。

拓展的 E-R 特性（Advanced Topics）

1. 特化（Specialization）

在实体集内部根据某些条件进行分组的过程称为特化。

🌰 例如：person 可以根据职位分成 student 和 employee 两个组，而 employee 又可以分为 instructor 和 secretary 两个组。

  • 自顶向下的设计过程，一个实体集可以分为多个子集。类比面向对象设计中的继承。

  • 这些子集变成更低层的实体集，会包含一些高层实体集没有的属性，参与一些高层实体集没有的联系。

  • 由标记为 ISA 的三角形组件描述。

  • 属性的继承（Attribute inheritance）：低层的实体集自动继承了其对应的高层实体集的所有属性和联系。

  • 重叠特化（Overlapping Specialization）：一个实体集可能属于多个特化实体集。例如，一个特定的雇员可以既是一个临时的雇员，又是一个秘书。

  • 不相交特化（Disjoint Specialization）：一个实体集必须属于至多一个特化实体集。

2. 概化（Generalization）

将一些具有相同属性的实体集合并成一个更高级别的实体集的过程称为概化。

  • 自底向上的设计过程。

  • 特化和概化是两个互逆的操作。在ER图中表示方法相同。

  • 特化和概化可以互换。

  • 概化的进行基于这样的认识：一定数量的实体集共享一些共同的特征（即用相同的属性描述它们,且它们都参与到相同的联系集中）。概化是在这些实体集的共性的基础上将它们综合成一个高层实体集。概化用于强调低层实体集间的相似性并隐藏它们的差异；由于共享属性的不重复出现，它还使得表达简洁。

3. 聚集（Aggregation）

聚集是一种抽象，通过这种抽象，联系被视为高层实体。可以表达联系间的联系。

🌰 例如：

eval_for 中的每个 instructor，student，project 组合肯定在 proj_guide 中，造成数据冗余。

一个学生在一个特定的项目中受一名老师指导。

学生、老师和项目的组合关联一个评估实体。

聚集之后的高层实体集 proj_guide 可以当作其他实体集处理。

关系数据库设计（Relational Database Design）

好的关系设计特点（Features of Good Relational Design）

有损分解（A Lossy Decomposition）：原表经过分解之后进行自然连接，如果形成的表与原表相同则为无损分解；否则为有损分解

原子域和第一范式（Atomic Domains and First Normal Form）

一个域是原子的（atomic ），如果该域的元素被认为是不可分的单元。

我们称一个关系模式 R 属于第一范式（First Normal Form，1NF），如果 R 的所有属性的域都是原子的。

使用函数依赖进行分解（Decomposition Using Functional Dependencies）

函数依赖（Functional Dependencies）

  • 定义：

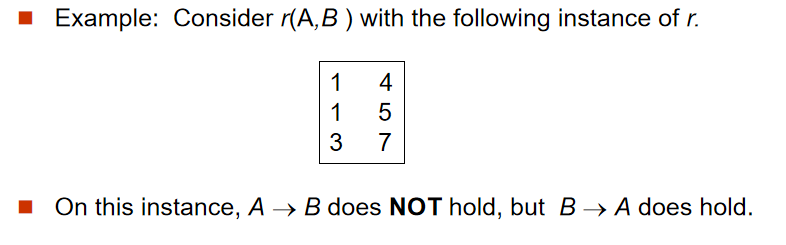
    • 对于联系 R ，如果有属性集合 $ \alpha \subseteq R$ ，$ \beta \subseteq R $ ，给定 r(R) 的一个实例，我们说这个实例满足函数依赖 $ \alpha \rightarrow \beta $ 的条件是：对实例中所有元组对 t1 和 t2，若 t1[ $ \alpha $ ] = t2[ $ \alpha $ ]，则 t1[ $ \beta $ ] = t2[ $ \beta $ ]

    • 如果在 r(R) 的每个合法实例中都满足函数依赖 $ \alpha \rightarrow \beta $ ，则我们说函数依赖在模式 r(R) 上成立（hold）。

  • 是合法关系上的约束

  • 一个属性集上的取值应该可以唯一确定另外一组属性上的取值

  • 函数依赖是码约束的泛化

  • 函数依赖能使我们表达超码表达不了的约束

  • 码的函数依赖

    • 超码（super key）：$ K \rightarrow R $
    • 候选码（candidate key）： $ K \rightarrow R $ and for no $ \alpha \subset K $ ，$ \alpha \rightarrow R $ （没有元组子集能蕴含 R）

  • 平凡函数依赖（trivial）：在所有关系中都满足

    • $ \alpha \rightarrow \alpha $

    • $ \alpha \rightarrow \beta $， if $ \beta \subseteq \alpha $

  • 函数依赖的闭包（closure）

    • 给定一个函数依赖集 $ F $，有可能会推断出某些其他的函数依赖。
    • 由 $ F $ 推断出来的所有依赖构成 $ F $ 的闭包，记作 $ F^+ $
    • $ F^+ $ 是 $ F $ 的超集

Boyce Codd 范式

  • 定义：具有函数依赖集 $ F $ 的关系模式 $ R $ 属于 $ BCNF $ 的条件是，对 $ F^+ $ 中所有形如 $ \alpha \rightarrow \beta $ 的函数依赖（其中 $ \alpha \subseteq R$ ，$ \beta \subseteq R $ ），下面至少有一项成立：

    • $ \alpha \rightarrow \beta $ 是平凡的函数依赖，（即， $ \beta \subseteq \alpha $）
    • $ \alpha $ 是模式 $ R $ 的一个超码

  • BC范式是我们能达到的比较满意的范式之一。它能消除所有利用函数依赖发现的冗余。

  • 一个数据库设计属于$ BCNF$ 的条件是，构成该设计的关系模式集中的每个模式都属于 \(BCNF\)。

  • 将模式分解成BCNF（Decomposing a Schema into BCNF）

    • 设 \(R\) 为不属于 \(BCNF\) 的一个模式。则存在至少一个非平凡的函数依赖 $ \alpha \rightarrow \beta $ ，其中 $ \alpha $ 不是 \(R\) 的超码。我们在设计中用一下两个模式取代 \(R\)。形成两个模式。
      • $ \left( \alpha \cup \beta \right) $
      • $ \left( R-\left( \beta -\alpha \right) \right) $
    • 当我们分解不属于 \(BCNF\) 的模式时，产生的模式中可能有一个或多个不属于 \(BCNF\)。在这种情况中，需要进一步分解，其最终结果是一个 \(BCNF\) 模式集合。

  • BCNF 和保持依赖

    • 如果分解后，每个依赖都得以保存，则称该分解为依赖保持分解。
    • 由于常常希望保持依赖，因此我们考虑另外一种比 $BCNF $ 弱的范式它允许我们保持依赖。该范式称为第三范式。

第三范式（third normal form）

  • 定义：具有函数依赖集 \(F\) 的关系模式 \(R\) 属于第三范式（third normal form）的条件是：对于 \(F^+\) 中所有形如 \(\alpha \rightarrow \beta\) 的函数依赖(其中 $ \alpha \subseteq R$ ，$ \beta \subseteq R $ )，以下至少一项成立:

    • \(\alpha \rightarrow \beta\) 是一个平凡的函数依赖
    • \(\alpha\) 是 \(R\) 的一个超码
    • \(\beta - \alpha\) 中的每个属性 \(A\) 都包含于 \(R\) 的一个候选码中

  • 注意上面的第三个条件并没有说单个候选码必须包含 \(\beta - \alpha\) 中的所有属；\(\beta - \alpha\)中 的每个属性 A 可能包含于不同的候选码中。

  • 注意任何满足 \(BCNF\) 的模式也满足 \(3NF\)，\(BCNF\) 是比 \(3NF\) 更严格的范式。

  • \(3NF\) 的定义允许某些 \(BCNF\) 中不允许的函数依赖。

函数依赖理论（Functional Dependency Theory）

阿姆斯特朗公理（Armstrong’s Axioms）

  • 自反律（reflexivity rule）：若 \(\alpha\) 为一属性集且 $ \beta \subseteq \alpha $ ，则 \(\alpha \rightarrow \beta\) 成立。
  • 增补律（augmentation rule）：若 \(\alpha \rightarrow \beta\) 成立且 \(\gamma\) 为一属性集，则 \(\gamma \alpha \rightarrow \gamma \beta\) 成立。
  • 传递律（transitivity rule）：若 \(\alpha \rightarrow \beta\) 和 \(\beta \rightarrow \gamma\) 成立，则 \(\alpha \rightarrow \gamma\) 成立。

根据以上三个公理可以推导出一些规则：

  • 合并律（union rule）：若 \(\alpha \rightarrow \beta\) 和 \(\alpha \rightarrow \gamma\) 成立，则 \(\alpha \rightarrow \beta \gamma\) 成立。

    🍗 证明：

    \(\alpha \rightarrow \beta\) （题目已知）1️⃣

    $ \alpha \gamma \rightarrow \beta \gamma$ （增补律）2️⃣

    \(\alpha \rightarrow \gamma\) （题目已知）3️⃣

    \(\alpha \alpha \rightarrow \alpha \gamma\) （增补律）4️⃣

    即 \(\alpha \rightarrow \alpha \gamma\) 5️⃣

    由 2️⃣ 和 5️⃣ 得 \(\alpha \rightarrow \beta \gamma\) （传递律）

  • 分解律（decomposition）：若 \(\alpha \rightarrow \beta \gamma\) 成立，则 \(\alpha \rightarrow \beta\) 和 \(\alpha \rightarrow \gamma\) 成立。

    🍖 证明：

    \(\alpha \rightarrow \beta \gamma\) （题目已知）1️⃣

    由 \(\beta \subseteq \beta \gamma\) 得 \(\beta \gamma \rightarrow \beta\) （自反律）2️⃣

    由 \(\gamma \subseteq \beta \gamma\) 得 \(\beta \gamma \rightarrow \gamma\) （自反律）3️⃣

    由 1️⃣ 和 2️⃣ 得 \(\alpha \rightarrow \beta\) （传递律）

    由 1️⃣ 和 3️⃣ 得 \(\alpha \rightarrow \gamma\) （传递律）

  • 伪传递律（pseudotransitivity rule）：若 \(\alpha \rightarrow \beta\) 和 \(\gamma \beta \rightarrow \delta\) 成立，则 \(\alpha \gamma \rightarrow \delta\) 成立。

    🍔 证明：

    \(\alpha \rightarrow \beta\) （题目已知）1️⃣

    \(\alpha \gamma \rightarrow \beta \gamma\) （增补律）2️⃣

    即 \(\alpha \gamma \rightarrow \gamma \beta\) 3️⃣

    \(\gamma \beta \rightarrow \delta\) （题目已知）4️⃣

    由 3️⃣ 和 4️⃣ 得 \(\alpha \gamma \rightarrow \delta\) （传递律）

属性集的闭包（Closure of Attribute Sets）

如果 \(\alpha \rightarrow \beta\) ，我们称属性 B 被 \(\alpha\) 函数确定（functionally determine）。要判断集合 \(\alpha\) 是否为超码，我们必须设计一个算法，用于计算被 \(\alpha\) 函数确定的属性集。一种方法是计算 \(F^+\)，找出所有左半部为 \(\alpha\) 的函数依赖，并合并这些函数依赖的右半部。但是这么做开销大，因为 \(F^+\) 可能很大。

令 \(\alpha\) 为一个属性集。我们将函数依赖集 \(F\) 下被 \(\alpha\) 函数确定的所有属性的集合称为 \(F\) 下 \(\alpha\) 的闭包，记为 \(\alpha ^+\) 。

设计一个算法：

🐍 实例模拟：

R = (A, B, C, G, H, I)
F = {A \(\rightarrow\) B A \(\rightarrow\) C CG \(\rightarrow\) H CG \(\rightarrow\) I B \(\rightarrow\) H}
$\left( AG \right) ^+ $

  1. result = AG
  2. result = ABCG (A \(\rightarrow\) C and A \(\rightarrow\) B)
  3. result = ABCGH (CG \(\rightarrow\) H and CG \(\subseteq\) AGBC)
  4. result = ABCGHI (CG \(\rightarrow\) I and CG \(\subseteq\) AGBCH)

故 \(AG\) 的闭包 \(AG^+\) 为 ABCGHI

🌜 \(AG\) 是不是超码：看 \(AG^+\) 能否唯一区分 \(R\) 的元组，即判断 \(R\) 是否包含于 \(AG^+\) 。由于 \(R \subseteq AG ^+\) ，得 \(AG\) 是超码

🌛 \(AG\) 是不是候选码：对 \(AG\) 的所有真子集求闭包，如果存在一个真子集的闭包可以唯一区分 \(R\) 的元组，则不是候选码。

🔔 属性闭包的多种用途：

1️⃣ 为了判断 \(\alpha\) 是否为超码，我们计算 \(\alpha^+\) ，检查 \(\alpha^+\) 是否包含 \(R\) 中的所有属性
2️⃣ 通过检查是否 \(\beta \subseteq \alpha^+\) ，我们可以检查函数依赖 \(\alpha \rightarrow \beta\) 是否成立(或换句话说，是否属于 \(F^+\))。也就是说，我们用属性闭包计算 \(\alpha^+\)，看它是否包含 \(\beta\)。
3️⃣ 该算法给了我们另一种计算 \(F^+\) 的方法：对任意的 \(\gamma \subseteq R\)，我们找出闭包 \(\gamma^+\)；对任意的 \(S \subseteq \gamma^+\)，我们输出一个函数依赖 \(S \subseteq \gamma^+\)

🌌 候选键的计算：

  • 定义：

    • 左部属性，只出现在 F 左边的属性
    • 右部属性，只出现在 F 右边的属性
    • 双部属性，出现在 F 两边的属性
    • 外部属性，不出现在 F 中的属性

  • 定理：

    • 左部属性一定出现在任何候选码中
    • 右部属性一定不出现在任何候选码中
    • 外部属性一定出现在任何候选码中
    • 双部属性可能出现在候选码中

  • 求所有候选键可以通过左部属性与每一个双部属性组合然后求闭包。也要单独考虑双部属性是不是候选码。

正则覆盖（Canonical Cover）

  • 无关属性（Extraneous Attribute）：

    • 定义：如果去除函数依赖中的一个属性不改变该函数依赖集的闭包，则称该属性是无关的

    • 形式化定义：考虑函数依赖集 \(F\) 及 \(F\) 中的函数依赖 \(\alpha \rightarrow \beta\)

      • 如果 \(A \in \alpha\) 并且 \(F\) 逻辑蕴含

        \[\left( F-\left\{ \alpha \rightarrow \beta \right\} \right) \cup \left\{ \left( \alpha -A \right) \rightarrow \beta \right\} \]

        则属性 \(A\) 在 \(\alpha\) 中是无关的。

      • 如果 \(A \in \beta\) 并且函数依赖集

        \[\left( F-\left\{ \alpha \rightarrow \beta \right\} \right) \cup \left\{ \alpha \rightarrow \left( \beta -A \right) \right\} \]

        逻辑蕴含 \(F\) ，则属性 \(A\) 在 \(\beta\) 中是无关的。

    • 无关属性只可能出现在依赖一段超过一个属性的情况下。🌰 例如，假定我们在 \(F\) 中有函数依赖 AB→C 和 A→C，那么 B 在AB→C 中是无关的。再比如，假定我们在F中有函数依赖 AB→CD 和 A→C，那么 C 在 AB→CD 的右半部中是无关的。

  • 正则覆盖（Canonical Cover）\(F_c\) 是与 \(F\) 等价的最小的函数依赖集合。

    • \(F_c\) 是一个依赖集，使得 \(F\) 中逻辑蕴含 \(F_c\) 中的所有依赖，并且 \(F_c\) 逻辑蕴含 \(F\) 中的所有依赖。
    • \(F_c\) 中任何函数依赖都不含无关属性。
    • \(F_c\) 中函数依赖的左半部都是唯一的。即，\(F_c\) 中不存在两个依赖 \(\alpha_1 \rightarrow \beta_1\) 和 \(\alpha_2 \rightarrow \beta_2\) ，满足 \(\alpha_1 = \alpha_2\) 。

  • 计算无关属性（Computing a Extraneous Attribute）

    • 左边属性无关：\(A \in \alpha\) ，\(A\) 疑似为无关属性。在 \(F\) 上计算

      \[\left( \left\{ \alpha \right\} -A \right) ^+ \]

      如果该闭包中包含 \(\beta\) 则说明 \(A\) 是 \(\alpha\) 中的无关属性。

    • 右边属性无关：$ A \in \beta$ ，\(A\) 疑似为无关属性。在

      \[F'= \left( F-\left\{ \alpha \rightarrow \beta \right\} \right) \cup \left\{ \alpha \rightarrow \left( \beta -A \right) \right\} \]

      上计算 $ \alpha^+$ ，如果该闭包中包含 \(\beta\) 则 \(A\) 是 \(\beta\) 中的无关属性。

  • 计算正则覆盖（Computing a Canonical Cover）

    • 合并相同的左部属性。
    • 计算无关属性（先左再右）并删除。
    • 循环直到 \(F_c\) 不变。
    • 由于顺序不同，计算出的正则覆盖可能不同。

🐍 实例模拟：

R = (A, B, C)

F = {A \(\rightarrow\) BC，B \(\rightarrow\) C，A \(\rightarrow\) B，AB \(\rightarrow\) C}

1️⃣ 合并 A \(\rightarrow\) BC，A \(\rightarrow\) B 得到 A \(\rightarrow\) BC，F = {A \(\rightarrow\) BC，B \(\rightarrow\) C，AB \(\rightarrow\) C}

2️⃣ 检查 A 是不是 AB \(\rightarrow\) C 中的无关属性。\(\left( \alpha - A \right) = B\) ，\(\left(\alpha - A \right)^+=BC\) 包含 \(\beta = C\) ，则 A 是无关属性，去掉 A 得 B \(\rightarrow\) C

3️⃣ F = {A \(\rightarrow\) BC，B \(\rightarrow\) C}

4️⃣ 考虑 C 是不是 A \(\rightarrow\) BC 中的无关属性。$ F' $ = {B \(\rightarrow\) C，A \(\rightarrow\) B}，\(\alpha=A\) ，\(\alpha^+\)=ABC 包含 \(\beta=BC\) ，则 C 是无关属性，去掉 C 得 A \(\rightarrow\) B

5️⃣ F = {A \(\rightarrow\) B，B \(\rightarrow\) C}

无损分解（lossless decomposition）

  • 定义：令 \(r \left( R \right)\) 为一个关系模式，F 为 \(r \left( R \right)\) 上的函数依赖集。令 \(R_1\) 和 \(R_2\) 为 R 的分解。如果用两个关系模式 $r_1 \left( R_1 \right) $ 和 $r_2 \left( R_2 \right) $替代 \(r \left( R \right)\) 时没有信息损失，则我们称该分解是无损分解（lossless decomposition）。更

  • 判断无损分解：$ r=\prod\nolimits_{R_1}^{}{\left( r \right) \Join}\prod\nolimits_{R_2}^{}{\left( r \right)} $

    我们可以用函数依赖来说明什么情况下分解是无损的。令\(R_1\)，和 \(R_2\) ，是 \(R\) 的无损分解，如果以下函数依赖中至少有一个属于 \(F^+\) ：

    • \(R_1 \cap R_2 \rightarrow R_1\)
    • \(R_1 \cap R_2 \rightarrow R_2\)

    换句话说，如果 \(R_1 \cap R_2\) 是 \(R_1\) 或 \(R_2\) 的超码，\(R\) 上的分解就是无损分解。

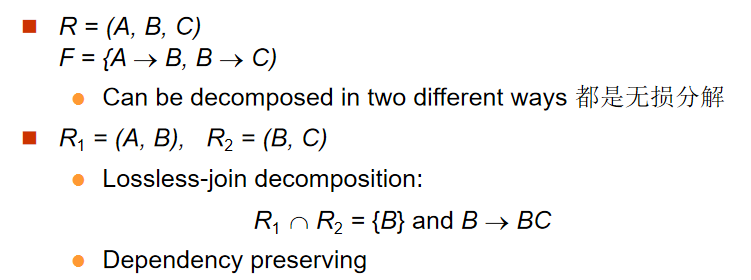
  • 无损分解可能造成没有保持依赖

  • 判断保持依赖算法（多项式时间）

分解算法（Decomposition Algorithm）

BCNF 分解

  • BCNF 的定义可以直接用于检查一个关系是否属于 BCNF。但是，计算 \(F^+\) 是一个繁重的任务。在某些情况下，判定一个关系是否属于BCNF可以作如下简化，只能分解之前使用：

    • 为了检查非平凡的函数依赖 α→β 是否违反 BCNF，计算 \(\alpha^+\)( α的属性闭包)，并且验证它是否包含 R 中的所有属性，即验证它是否是 R 的超码。
    • 检查关系模式 R 是否属于 BCNF，仅须检查给定集合 F 中的函数依赖是否违反 BCNF 就足够了，不用检查 \(F^+\) 中的所有函数依赖。

  • 当一个关系分解后，后一步过程就不再适用。也就是说，当我们判定 R 上的一个分解 \(R_i\) 是否违反 BCNF 时，只用 \(F\) 就不够了，只能在 \(F^+\) 的范围。

  • BCNF 分解算法：保证无损分解，无法保证依赖保持

    🐍 实例模拟：

🔔 很多时候我们能够得到BCNF分解，但是却无法做到依赖保持

3NF 分解：

  • 3NF 是 BCNF 的放松，允许一些冗余的存在

  • 3NF 分解算法：保证无损分解，也保证依赖保持

  1. 先求出正则覆盖 \(F_c\)
  2. 对于 \(F_c\) 里面的所有函数依赖 a->b，均转化为 \(R_i=ab\)
  3. 对于所有的模式 \(R_i\)
    • 如果包含候选码，进行第 4
    • 如果都不包含候选码， 将任意一个候选码添加到模式 \(R_i\) 里面
  4. 如果一个模式被另一个模式包含，则去掉此被包含的模式。

事务（Transactions）

事务的概念（Transaction Concept）

事务是访问并可能更新各种数据项的一个程序执行单元( unit )。

事物的状态（Transaction State）

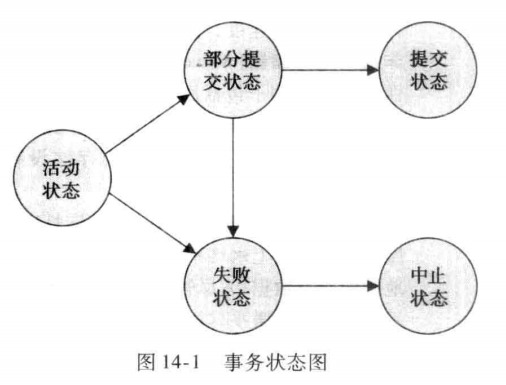
  • 活动的（active）：初始状态，事务执行时处于这个状态。
  • 部分提交的（partially committed）：最后一条语句执行后。
  • 失败的（failed）：发现正常的执行不能继续后。
  • 中止的（aborted）：事务回滚并且数据库已恢复到事务开始执行前的状态后。
  • 提交的（committed）：成功完成后。

串行化（Serializability）

冲突可串行化（Conflict Serializability）

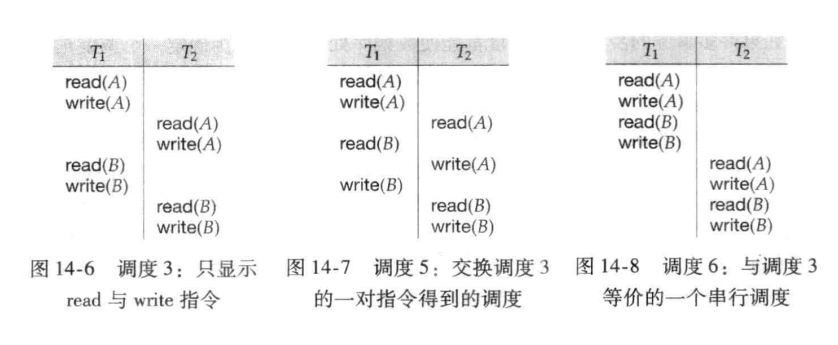
  • 考虑一个调度 \(S\)，其中含有分别属于 \(I\) 与 \(J\) 的两条连续指令 \(I_i\) 与 \(I_j\)，如果 \(I\) 与 \(J\) 引用不同的数据项，则交换 \(I\)与 \(J\) 不会影响调度中任何指令的结果。
  • 如果 \(I\) 与 \(J\) 引用相同的数据项，只有读读的时候顺序无所谓，读写和写写的顺序都不能变。

🔔 优先图判断冲突可串行化
根据不同事物对同一资源的读写顺序画出优先图，如果没有环路，则冲突可串行化。
该图由两部分组成 \(G=(V,E)\) ，其中 \(V\) 是顶点集，\(E\) 是边集，顶点集由所有参与调度的事物组成，边集由满足一下三个条件之一的边 \(T_i \rightarrow T_j\) 组成：

  • 在 \(T_j\) 执行 \(read(Q)\) 之前，\(T_i\) 执行 \(write(Q)\)
  • 在 \(T_j\) 执行 \(write(Q)\) 之前，\(T_i\) 执行 \(read(Q)\)
  • 在 \(T_j\) 执行 \(write(Q)\) 之前，\(T_i\) 执行 \(write(Q)\)

如果优先图中存在边 \(T_i \rightarrow T_j\)，则在任何等价于 \(S\) 的串行调度 \(S'\) 中，\(T_i\) 必出现在 \(T_j\) 之前。

🍎 调度顺序：拓扑排序

可恢复调度（recoverable schedule）

一个可恢复调度（recoverable schedule）应满足：对于每对事务 \(T_i\) 和 \(T_j\)，如果 \(T_j\) 读取了之前由 \(T_i\) 所写的数据项，则 \(T_i\) 先于 \(T_j\)提交。例如，调度 9 是不可恢复调度的一个例子，如果要使调度 9 是可恢复的，则 \(T_7\) ，应该推迟到 \(T_6\) 提交后再提交(仅强调提交顺序)。

无级联调度（cascadeless schedule）

级联回滚（cascading rollback）：考虑图14-15所示的部分调度。事务 \(T_8\) 写入 A 的值，事务 \(T_9\) 读取了 A 的值。事务 \(T_9\) 写人 A 的值，事务 \(T_10\) 读取了 A 的值。假定此时事务 \(T_8\) 失败，\(T_8\) 必须回滚。由于 \(T_9\) 依赖于 \(T_8\)，因此事务 \(T_9\) 必须回滚。由于 \(T_{10}\) 依赖于 \(T_9\)，因此 \(T_{10}\) 必须回滚。这种因单个事务故障导致一系列事务回滚的现象称为级联回滚（cascading rollback）。

级联回滚导致撤销大量工作，是我们不希望发生的。我们希望对调度加以限制，避免级联回滚发生。这样的调度称为无级联调度。规范地说，无级联调度（cascadeless schedule）应满足：对于每对事务 \(T_i\) 和 \(T_j\)，如果 \(T_j\) 读取了先前由 \(T_i\) 所写的数据项，则 \(T_i\) 必须在 \(T_j\) 这一读操作前提交(强调读和提交的顺序)。容易验证每一个无级联调度也都是可恢复的调度。

并发控制（Concurrency Control）

锁（Lock）

排他锁：如果当前指令对数据项获得排他锁，则该指令对数据项既可以读也可以写。

共享锁：如果当前指令对数据项获得共享锁，则该指令对数据项只能进行读操作。

许多事务可以同时持有一个数据项上的共享锁，但是只有当其他事务在一个数据项上不持有任何锁（无论共享锁或排他锁）时，一个事务才允许持有该数据项上的排他锁。

锁协议（Locking Protocol）

两阶段封锁协议（two-phase locking protocol）：该协议要求每个事务分两个阶段提出加锁和解锁申请。

  • 增长阶段（growing phase）：事务可以获得锁，但不能释放锁。
  • 缩减阶段（shrinking phase）：事务可以释放锁，但不能获得新锁。

严格两阶段封锁协议（strict two-phase locking protocol）：这个协议除了要求封锁是两阶段之外，还要求事务持有的所有排他锁必须在事务提交后方可释放。这个要求保证未提交事务所写的任何数据在该事务提交之前均以排他方式加锁，防止其他事务读这些数据。可以避免级联回滚。

强两阶段封锁协议（rigorous two-phase locking protocol）：要求事务提交之前不能释放任何锁。

锁转换（lock conversion）：

  • 升级（upgrade）：共享锁 -> 排他锁，只能发生在增长阶段。
  • 降级（downgrade）：排他锁 -> 共享锁，只能发生在缩减阶段。

死锁检测（Deadlock Detection）

死锁可以用称为等待图（wait-for graph）的有向图来精确描述。该图由 \(G=(V，E)\) 对组成，其中 \(V\) 是顶点集，\(E\) 是边集。顶点集由系统中的所有事务组成，边集 \(E\) 的每一元素是一个有序对 \(T_i \rightarrow T_j\)。如果 \(T_i \rightarrow T_j\) 属于 \(E\)，则存在从事务 \(T_i\) 到 \(T_j\) 的一条有向边，表示事务 \(T_i\) 在等待 \(T_j\) 释放所需数据项。

当事务 \(T_i\) 申请的数据项当前被 \(T_j\) 持有时，边 \(T_i \rightarrow T_j\) 被插入等待图中。只有当事务 \(T_j\) 不再持有事务 \(T_i\) 所需数据项时,这条边才从等待图中删除。

当且仅当等待图包含环时，系统中存在死锁。在该环中的每个事务称为处于死锁。要检测死锁，系统需要维护等待图，并周期性地激活一个在等待图中搜索环的算法。
posted @ 2022-07-14 14:36  gonghr  阅读(6711)  评论(0)  编辑  收藏  举报