离散数学（格与布尔代数）
格
是格(L，≤)的子格。
格的定义
偏序格
定义：给出一个偏序集（L,≤）,如果对于任意a,b∈L，L的子集{a, b}在L中都有一个最大下界(记为inf{a, b})和一个最小上界(记为sup{a, b}) 则称（L，≤）为一个格。
🔔 全序集是一个格，不是所有偏序集都是格.
是格：
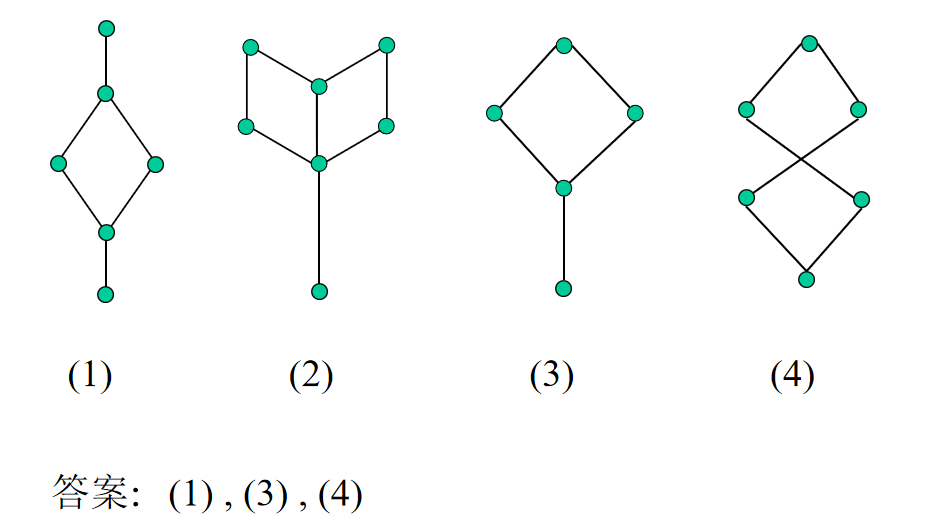
不是格：
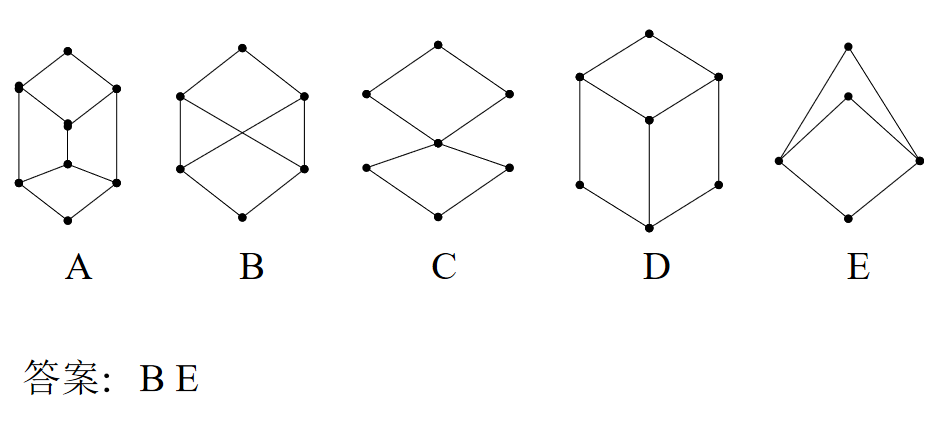
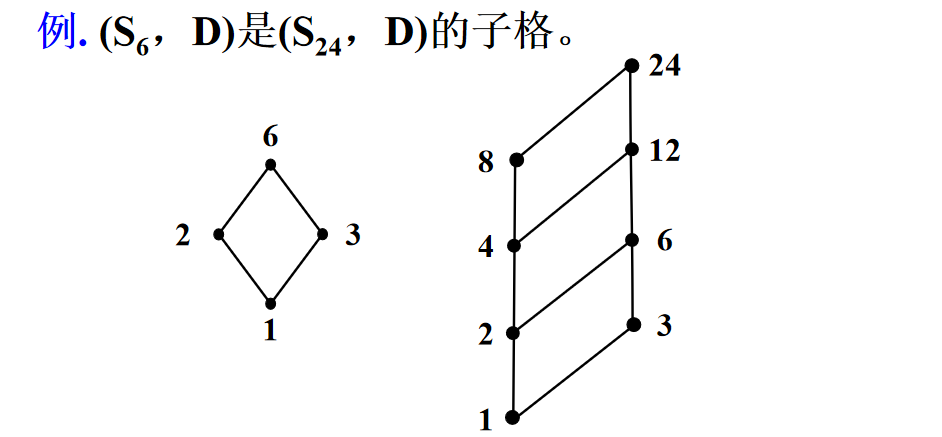
偏序子格
定义：设(L，≤)是格，S ⊆ L，如果(S，≤)是格，则称(S，≤)是格(L，≤)的子格。
代数格
定义：设L是一个集合，×，⊕是L上两个二元代数运算，如果这两种运算对于L中元素满足：
- 交换律：a×b=b×a，a⊕b=b⊕a。
- 结合律：a ×（b×c）=（a×b）× c，
a ⊕（b⊕c）=（a⊕b）⊕ c。 - 吸收律：a ×（a⊕b）= a，
a ⊕（a×b）= a。
则称此代数系统(L，×，⊕)为一个格。
🔔
1️⃣ 设(L, ×, ⊕)是格,则(L, ×)和(L, ⊕) 为交换半群
2️⃣ 满足吸收律可推出它们一定满足幂等律。
代数子格
设(L,×,⊕)是一个代数格，S ⊆ L，(S,×,⊕)称为(L,×,⊕)的一个子格，当且仅当在运算×,⊕下，S是封闭的。
🔔 (S,×,⊕)是格(L,×,⊕)的子格的充要条件是: S ⊆ L 且（S,×,⊕）是一个格。
代数格与偏序格的等价性
定义：一个偏序格必是一个代数格；反之亦然.
代数子格与偏序子格的关系
-
若(S,×,⊕)是(L, ×, ⊕)的代数子格，则(S，≤）是 (L，≤)的偏序子格；
-
若(S，≤)是(L，≤)的偏序子格，则(S,×,⊕) 不一定是(L, ×, ⊕)的代数子格。 （因为代数子格必须满足封闭性）
格的性质
格的其他性质
1️⃣ 设(L，≤)是一个格，a，b是 L 中任意元素，于是 a≤b <=> a×b = a <=> a ⊕ b = b
2️⃣ 设(L，≤)是一个格，a，b，c是 L 中任意元素，如果b≤c，则有 a×b ≤ a×c，a⊕b ≤ a⊕c
3️⃣ 设(L，≤)是一个格，a，b，c是L中任意元素。于是有分配不等式
- a⊕(b×c) ≤ (a⊕b)×(a⊕c)
- a×(b⊕c) ≥ (a×b)⊕(a×c)
（记忆方法：最后进行 ⊕ 的式子小）
🔔 在一般格中，分配律不是总成立的，但上述分配不等式总是成立的。
4️⃣ 设（L，≤）是一个格，a，b，c是 L 中任意元素，于是，a≤b <=> a⊕(b×c) ≤ b×(a⊕c)
格的同态和同构
1️⃣ 设(L,×,⊕)和(S,∧,∨)是两个格，L到S内的映射g称为(L,×,⊕)到(S,∧,∨)的格同态映射，如果对任意a，b∈L，都有
- g(a×b)= g(a)∧g(b)
- g(a⊕b) = g(a)∨g(b).
2️⃣ 格 L 到 L 内的同态映射称为格的自同态映射
3️⃣ 若 g 是 L 到 S 上的同态映射，且是一对一的，则称 g 是格同构映射，并称格 L 与格 S 是同构的。
此时，对任意 x∈L，任意 y∈S ，有 g-1(g(x))=x，g(g-1(y))=y。
4️⃣ 格的同态映射一定是保序映射，但保序不一定是同态
设(L,×,⊕) ≡ (L, ≤)和(S,∧,∨) ≡ (S, ≤)是两个格。如果 g 是 L 到 S 内的同态映射，则 g 是保序映射，
亦即，对任意 a，b∈L，若a≤b，则g(a)≤g(b)。
5️⃣ 设(L,×,⊕)是一个格，g 是此格的自同态映射，于是 g(L)是(L, ×, ⊕)的代数子格。
6️⃣ 设(L,×,⊕), (S,∧,∨)是两个格，若 g 是 L 到 S 上的同构映射,则 g 的逆映射 g-1 是 S 到 L 上的同构映射。
7️⃣ 若格（L，×，⊕) ≡ (L, ≤)和格(S，∧，∨) ≡ (S, ≤) 同构 ，g 是其同构映射, 则对 L 中任意两个元素a，b，有a≤b <=> g(a)≤g(b)
n 维格
几种特殊的格
有界格
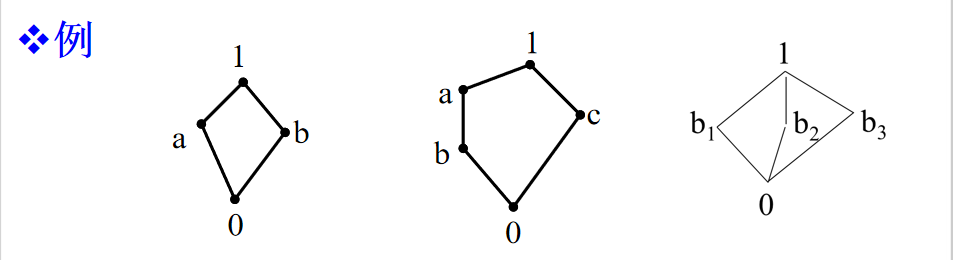
定义：格(L，≤)称为有界格，如果它有一个最大元素(记为1)和一个最小元素(记为0)，亦即，对任意a∈L，都有 0≤a≤1, 0，1称为格 (L，≤)的界。
🔔 有限格必是有界格，有界格不一定是有限格
1️⃣ 若(L,×,⊕, 0, 1)是有界格，则对任意a∈L，恒有
a ⊕ 0 = a， a × 1 = a，
a ⊕ 1 = 1， a × 0 = 0。
2️⃣ 余元素：在有界格(L，×，⊕，0，1)中，一个元素b∈L，称为元素a∈L的余元素，如果a × b = 0， a ⊕ b = 1。
3️⃣ 在有界格中，一元素可能没有余元素；如果有余元素，可以有一个或一个以上的余元素.
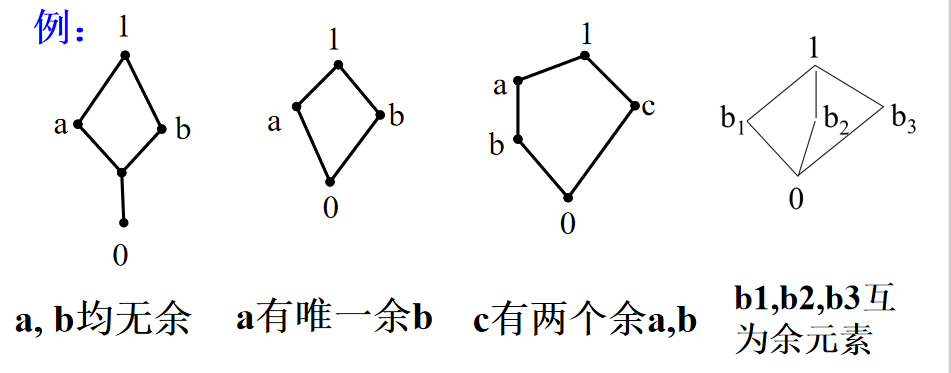
4️⃣ 在有界格（L,×,⊕, 0, 1)中，1是0的唯一 一个余元素，反之亦然。
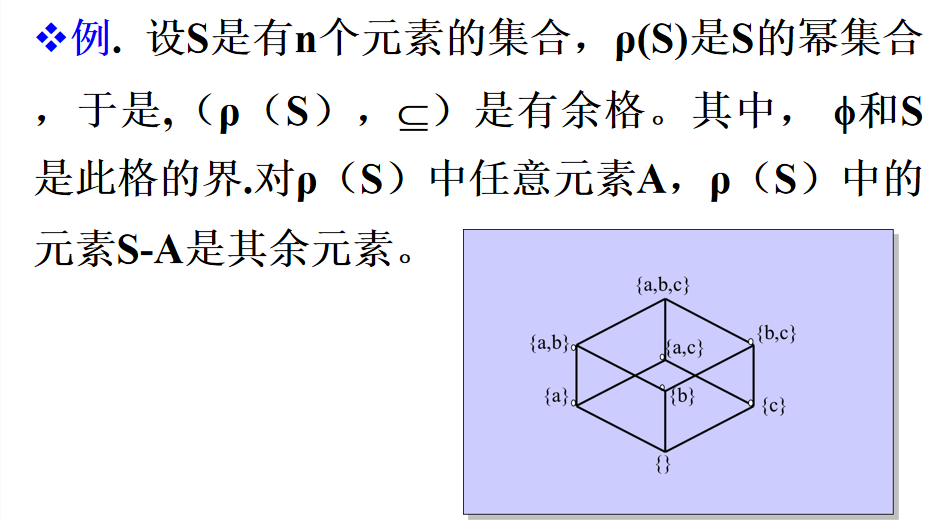
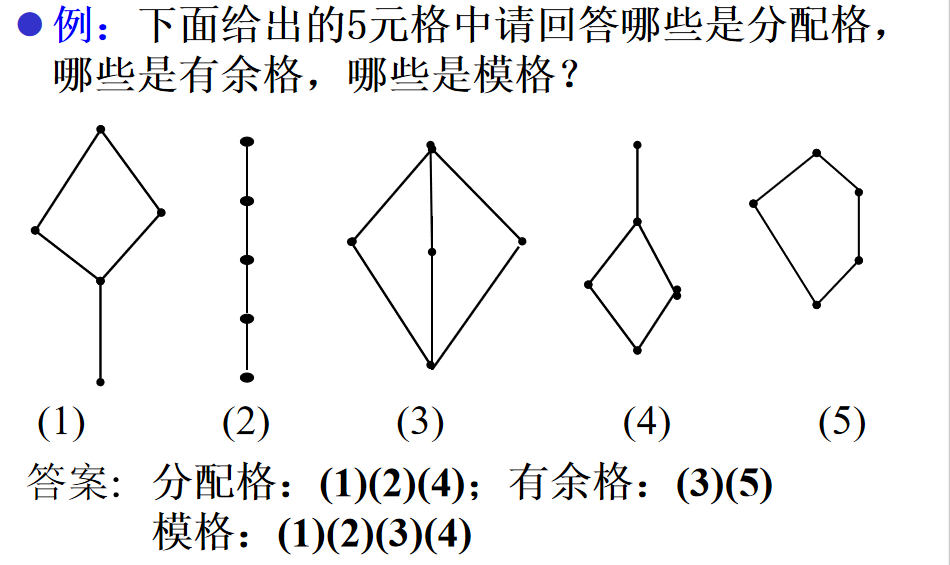
有余格
定义：称有界格(L，×，⊕，0，1)是一个有余格如果对 L 中每一个元素，都至少有一个余元素。
分配格
定义：格(L,×,⊕)称为分配格，如果对任意 a，b，c∈L，恒有
a×(b⊕c) = (a×b)⊕(a×c)
a⊕(b×c) = (a⊕b)×(a⊕c)
🔔
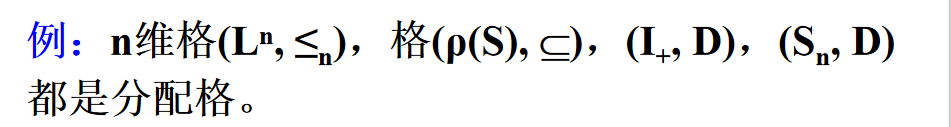
1️⃣ 分配格定义中的两个等式是等价的，可以互相推出
2️⃣ 但不是所有的格都是分配格
3️⃣ 分配格的任意子格仍是分配格。
‼️ L是分配格当且仅当 L 既不含有与五角格同构的子格;也不含有与钻石格同构的子格。
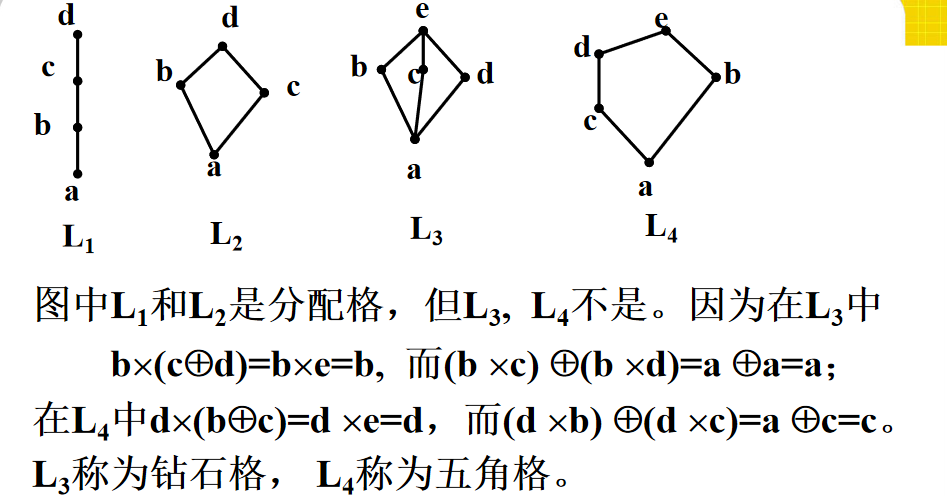
5️⃣ 任意一个链都是一个分配格
6️⃣ (德摩根定律) 设(L,×,⊕)是一个分配格，对任意a, b∈L，若a，b有余元素a’, b’，则
(a×b)’= a’⊕b’ (a⊕b)’= a’×b’
7️⃣ 设格(L,×,⊕)是分配格，对任意a, b, c∈L，如果a×c = b×c，a⊕c = b⊕c，则a = b。
8️⃣ 设格(L,×,⊕)是一个有余分配格（有界分配格），则对任意a∈L，a 的余元素 a′ 是唯一的。
模格
定义：设(L,≤)是一个格，对任意a, b, c∈L，如果a≤b，都有a⊕(b×c)= b×(a⊕c)则称(L，≤)为模格。
🔔
1️⃣ 任意一个分配格都是模格
2️⃣ 模格不一定是分配格。
‼️
- 一个格 L 是模格当且仅当 L 不含与五角格同构的子格。
- 一个模格是分配格当且仅当 L 不含与钻石格同构的子格
4️⃣ 格(L，≤)是模格的充要条件是：
对任意a，b，c∈L，如果a≤b，a×c=b×c，a⊕c=b⊕c，则必有a=b。
布尔代数
布尔代数的定义及其性质
定义： 一个有余分配格是一个布尔代数。记为(B，·，+，ˉ，0，1)。
性质：
Huntington(亨廷顿)公理
定理: 设B是一个至少含有两个不同元素的集合，·，+是定义在B上的两种代数运算，如果对任意a，b，c∈B，满足下面公理：
子代数
任给一个布尔代数 (B, ·, +, ¯, 0, 1)。若B的一个子集S包含0和1, 且(S，·，+，¯，0，1)仍是一个布尔代数,则称S为B的子代数。
设（B，·，+，¯，0，1）是布尔代数.于是，B的子集S是B的子代数的充要条件是S在运算· ，+，¯ 下是封闭的。
往期回顾
离散数学（集合论）
离散数学（古典数理逻辑）
离散数学（图与网络）
离散数学（数论基础）
离散数学（格与布尔代数）
离散数学（群、环、域）
