【数据结构与算法】二叉树的 Morris 遍历（前序、中序、后序）

前置说明

不了解二叉树非递归遍历的可以看我之前的文章【数据结构与算法】二叉树模板及例题

Morris 遍历

概述

Morris 遍历是一种遍历二叉树的方式，并且时间复杂度O(N)，额外空间复杂度O(1) 。通过利用原树中大量空闲指针的方式，达到节省空间的目的

分析

设一棵二叉树有 n 个节点，则所有节点的指针域总和为 2 * n ，所有节点的非空指针域总和为 n - 1（非根节点被一个指针指向，根节点不被指针指向），所有节点的空指针域总和为 2n - (n - 1) = n + 1。

可以看到有大量的空指针域没有用到，在可以改变原二叉树结构的前提下，我们可以通过合理利用节点的空指针域，不开辟额外空间进行二叉树的非递归遍历。

❓ 那么先序、中序、后序遍历的节点访问顺序是如何确定的呢

如上图，根据紫色箭头顺序访问，第一次访问到的节点组成的集合就是先序遍历的结果。类似的，第二次访问到的节点组成的集合就是中序遍历的结果；第三次访问到的节点组成的集合就是后序遍历的结果。

通过设置节点访问不同次数的操作就可以实现三种遍历。

❓ Morris 遍历的实质：建立一种机制，对于没有左子树的节点只到达一次，对于有左子树的节点会到达两次

🔔 Morris 遍历的原则

假设来到当前节点 cur，开始时 cur 来到头节点位置

• 如果 cur 没有左孩子，cur向右移动(cur = cur.right)

• 如果 cur 有左孩子，找到左子树上最右的节点 mostRight

  • a.如果 mostRight 的右指针指向空，让其指向 cur， 然后 cur 向左移动(cur = cur.left)

  • b.如果 mostRight 的右指针指向 cur，让其指向 null， 然后 cur 向右移动(cur = cur.right)

• cur 为空时遍历停止

🌰 举个例子：

已访问节点次序：1

1️⃣ 首先 cur 来到头结点 1，按照 morris 原则的第二条第一点，它存在左孩子，cur 左子树上最右的节点为 5，它的 right 指针指向空，所以让其指向 1，cur 向左移动到2。
已访问节点次序：1 2

2️⃣ 2 有左孩子，且它左子树最右的节点 4 指向空，按照 morris 原则的第二条第一点,让 4 的 right 指针指向 2，cur 向左移动到 4
已访问节点次序：1 2 4

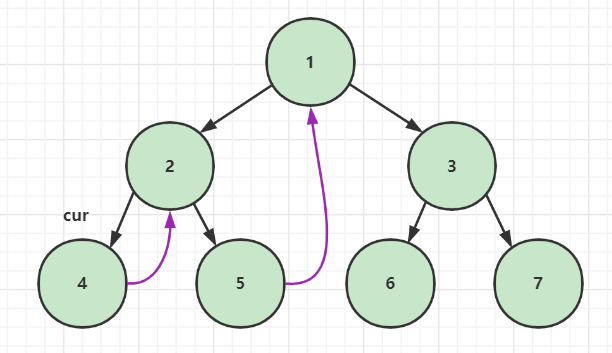
3️⃣ 4 不存在左孩子，按照 morris 原则的第一条，cur 向右移动，在第二步中，4 的 right 指针已经指向了 2，所以 cur 会回到 2
已访问节点次序：1 2 4 2

4️⃣ 重新回到 2，有左孩子，它左子树最右的节点为 4，但是在第二步中，4 的 right 指针已经指向了 2，不为空。所以按照 morris 原则的第二条第二点，cur 向右移动到 5，同时 4 的 right 指针重新指向空
已访问节点次序：1 2 4 2 5

5️⃣ 5 不存在左孩子，按照 morris 原则的第一条，cur 向右移动，在第一步中，5 的 right 指针已经指向了 1，所以 cur 会回到 1
已访问节点次序：1 2 4 2 5 1

6️⃣ cur 回到 1，回到头结点，左子树遍历完成，1 有左孩子，左子树上最右的节点为 5，它的 right 指针指向 1，按照 morris 原则的第二条第二点，cur 向右移动到 3，同时 5 的 right 指针重新指回空
已访问节点次序：1 2 4 2 5 1 3

7️⃣ 3 有左孩子，且它左子树最右的节点 6 指向空，按照 morris 原则的第二条第一点,让 6 的 right 指针指向 3，cur 向左移动到 6
已访问节点次序：1 2 4 2 5 1 3 6

8️⃣ 6 不存在左孩子，按照 morris 原则的第一条，cur 向右移动，在第二步中，6 的 right 指针已经指向了 3，所以 cur 会回到 3
已访问节点次序：1 2 4 2 5 1 3 6 3

9️⃣ 重新回到 3，有左孩子，它左子树最右的节点为 6，但是在第二步中，6 的 right 指针已经指向了 3，不为空。所以按照 morris 原则的第二条第二点，cur 向右移动到 7，同时 6 的 right 指针重新指向空
已访问节点次序：1 2 4 2 5 1 3 6 3 7

1️⃣0️⃣ cur 没有左孩子，向右移动到 null，遍历停止
最终已访问节点次序：1 2 4 2 5 1 3 6 3 7

可以发现，节点1 2 3（有左子树）被 cur 访问了两次，而节点4 5 6 7（没有左子树）被 cur 访问了一次。正好验证了之前提到的 Morris 遍历的机制：对于没有左子树的节点只到达一次，对于有左子树的节点会到达两次。

以上就是 Morris 遍历的全过程了，通过在遍历过程中适当的位置，即每个节点访问特定次数后设置操作，可以实现三种遍历

前序遍历

• 对于没有左子树的节点只到达一次，直接打印

• 对于有左子树的节点会到达两次，则在第一次到达时打印

public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    if (root != null) {
        TreeNode cur = root;
        TreeNode mostRight = null;
        while (cur != null) {
            // cur表示当前节点，mostRight表示cur的左孩子的最右节点
            mostRight = cur.left;
            if (mostRight != null) {
                // cur有左孩子，找到cur左子树最右节点
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                // mostRight的右孩子指向空，让其指向cur，cur向左移动
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    ans.add(cur.val);  // 此时第一次访问节点，记录答案
                    cur = cur.left;
                    continue;          // 直接进入下一次循环（容易忘）
                } else {
                    // mostRight的右孩子指向cur，让其指向空，cur向右移动
                    mostRight.right = null;
                    cur = cur.right;
                }
            } else {
                /// 没有左子树的节点只到达一次直接记录答案, cur 向右移动
                ans.add(cur.val);
                cur = cur.right;
            }
        }
    }
    return ans;
}

中序遍历

• 对于没有左子树的节点只到达一次，直接打印

• 对于有左子树的节点会到达两次，第二次到达时打印

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    if (root != null) {
        TreeNode cur = root;
        TreeNode mostRight = null;
        while (cur != null) {
            // cur表示当前节点，mostRight表示cur的左孩子的最右节点
            mostRight = cur.left;
            if (mostRight != null) {
                // cur有左孩子，找到cur左子树最右节点
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                // mostRight的右孩子指向空，让其指向cur，cur向左移动
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;            // 直接进入下一次循环（容易忘）
                } else {
                    ans.add(cur.val);        // 第二次到达，记录答案 
                    mostRight.right = null;  // mostRight的右孩子指向cur，让其指向空，cur向右移动     
                    cur = cur.right;
                }
            } else {
                ans.add(cur.val);   // 没有左子树的节点只到达一次直接记录答案, cur 向右移动
                cur = cur.right;
            }
        }
    }
    return ans;
}

后序遍历

• 第二次访问节点时逆序打印该节点左树的右边界

• 最后单独逆序打印整棵树的右边界

public List<Integer> postorderTraversal(TreeNode root) {
     if (root != null) {
        TreeNode cur = root;
        TreeNode mostRight = null;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                    printEdge(cur.left);     // 第二次访问时逆序打印该节点左树的右边界
                    cur = cur.right;
                }
            } else {
                cur = cur.right;
            }
        }
        printEdge(root);     // 最后单独打印整棵树的右边界
    }
    return ans;
}

public void printEdge(TreeNode node) {   // 逆序打印：反转链表打印后再反转回原样
    TreeNode tail = reverseEdge(node);
    TreeNode cur = tail;
    while (cur != null) {
        ans.add(cur.val);
        cur = cur.right;
    }
    reverseEdge(tail);
}

public TreeNode reverseEdge(TreeNode node) {  // 链表反转
    TreeNode pre = null;
    TreeNode next = null;
    while (node != null) {
        next = node.right;
        node.right = pre;
        pre = node;
        node = next;
    }
    return pre;
}