【数据结构与算法】Trie（前缀树）模板和例题
Trie 树的模板
Trie 树的简介
Trie树，又称字典树，单词查找树或者前缀树，是一种用于快速检索的多叉树结构，如英文字母的字典树是一个26叉树，数字的字典树是一个10叉树。他的核心思想是空间换时间，空间消耗大但是插入和查询有着很优秀的时间复杂度。
Trie 树的定义
Trie树的键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀（prefix）,从根节点到当前结点的路径上的所有字母组成当前位置的字符串，结点可以保存当前字符串、出现次数、指针数组(指向子树)以及是否是结尾标志等等。
🌈 简图
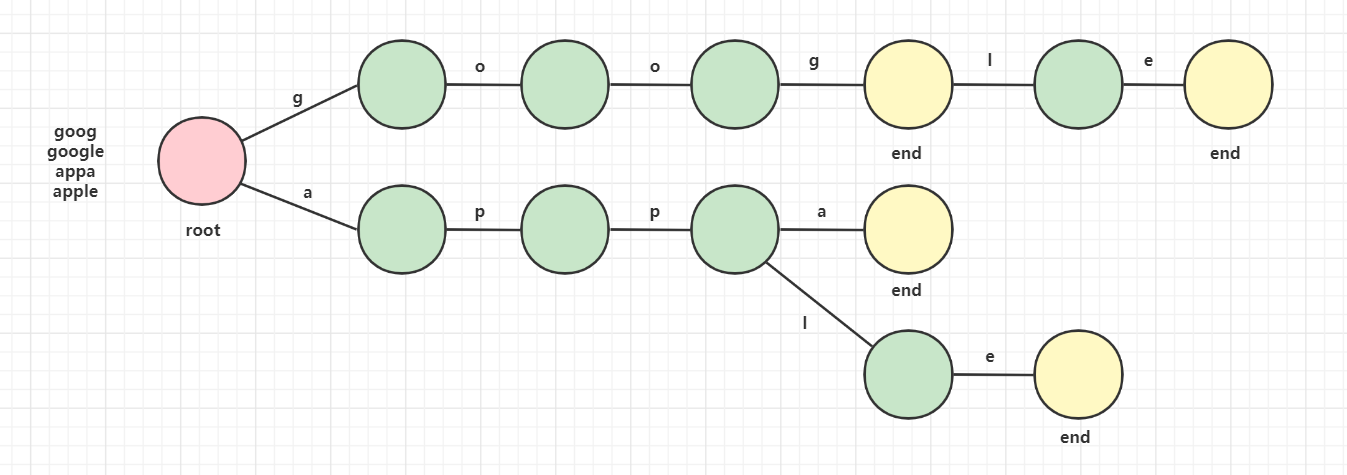
实际上每个节点有一个end属性和一个字典长度的节点数组
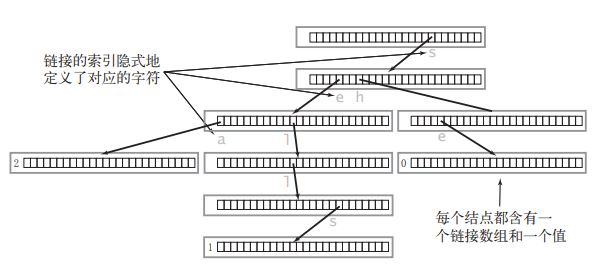
Trie 树的实现
Trie（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。
请你实现 Trie 类：
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。
示例：
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示：
1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次
class Trie {
class TrieNode {
boolean end;
TrieNode[] tns = new TrieNode[26];
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
TrieNode p = root;
for(int i = 0; i < word.length(); i++) {
int u = word.charAt(i) - 'a';
if(p.tns[u] == null) p.tns[u] = new TrieNode();
p = p.tns[u];
}
p.end = true;
}
public boolean search(String word) {
TrieNode p = root;
for(int i = 0; i < word.length(); i++) {
int u = word.charAt(i) - 'a';
if(p.tns[u] == null) return false;
p = p.tns[u];
}
return p.end;
}
public boolean startsWith(String prefix) {
TrieNode p = root;
for(int i = 0; i < prefix.length(); i++) {
int u = prefix.charAt(i) - 'a';
if(p.tns[u] == null) return false;
p = p.tns[u];
}
return true;
}
}
Trie 树的例题
LeetCode 211. 添加与搜索单词
请你设计一个数据结构，支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary ：
WordDictionary() 初始化词典对象
void addWord(word) 将 word 添加到数据结构中，之后可以对它进行匹配
bool search(word) 如果数据结构中存在字符串与 word 匹配，则返回 true ；否则，返回 false 。word 中可能包含一些 '.' ，每个 . 都可以表示任何一个字母。
示例：
输入：
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
输出：
[null,null,null,null,false,true,true,true]
解释：
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True
提示：
1 <= word.length <= 500
addWord 中的 word 由小写英文字母组成
search 中的 word 由 '.' 或小写英文字母组成
最多调用 50000 次 addWord 和 search
class WordDictionary {
class Node {
boolean end;
Node[] tns = new Node[26];
}
Node root;
public void insert(String s) {
Node p = root;
for(int i = 0; i < s.length(); i++) {
int u = s.charAt(i) - 'a';
if(p.tns[u] == null) p.tns[u] = new Node();
p = p.tns[u];
}
p.end = true;
}
public WordDictionary() {
root = new Node();
}
public void addWord(String word) {
insert(word);
}
public boolean search(String s) {
return dfs(s, root, 0);
}
public boolean dfs(String s, Node p, int idx) {
int n = s.length();
if(idx == n) return p.end;
char c = s.charAt(idx);
if(c == '.') {
for(int i = 0; i < 26; i++) {
if(p.tns[i] != null && dfs(s, p.tns[i], idx + 1)) return true;
}
return false;
}
else {
int u = c - 'a';
if(p.tns[u] == null) return false;
return dfs(s, p.tns[u], idx + 1);
}
}
}
LeetCode 720. 词典中最长的单词
给出一个字符串数组 words 组成的一本英语词典。返回 words 中最长的一个单词，该单词是由 words 词典中其他单词逐步添加一个字母组成。
若其中有多个可行的答案，则返回答案中字典序最小的单词。若无答案，则返回空字符串。
示例 1：
输入：words = ["w","wo","wor","worl", "world"]
输出："world"
解释： 单词"world"可由"w", "wo", "wor", 和 "worl"逐步添加一个字母组成。
示例 2：
输入：words = ["a", "banana", "app", "appl", "ap", "apply", "apple"]
输出："apple"
解释："apply" 和 "apple" 都能由词典中的单词组成。但是 "apple" 的字典序小于 "apply"
提示：
1 <= words.length <= 1000
1 <= words[i].length <= 30
所有输入的字符串 words[i] 都只包含小写字母。
class Solution {
class Trie {
class TrieNode {
boolean end;
TrieNode[] tns = new TrieNode[26];
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String s) {
TrieNode p = root;
for(int i = 0; i < s.length(); i++) {
int u = s.charAt(i) - 'a';
if(p.tns[u] == null) {
p.tns[u] = new TrieNode();
}
p = p.tns[u];
}
p.end = true;
}
public boolean search(String s) {
TrieNode p = root;
for(int i = 0; i < s.length(); i++) {
int u = s.charAt(i) - 'a';
if(p.tns[u] == null) return false;
p = p.tns[u];
}
return p.end;
}
public boolean startsWith(String s) {
TrieNode p = root;
for(int i = 0; i < s.length(); i++) {
int u = s.charAt(i) - 'a';
if(p.tns[u] == null) return false;
p = p.tns[u];
}
return true;
}
public boolean query(String s) {
TrieNode p = root;
for(int i = 0; i < s.length(); i++) {
int u = s.charAt(i) - 'a';
if(p.tns[u] == null) return false;
if(p.tns[u].end == false) return false;
p = p.tns[u];
}
return true;
}
}
public String longestWord(String[] words) {
Trie t = new Trie();
for(String word : words) {
t.insert(word);
}
String ans = "";
for(String word : words) {
int lena = ans.length();
int lenb = word.length();
if(lenb < lena) continue;
if(lenb == lena && word.compareTo(ans) > 0) continue;
if(t.query(word)) ans = word;
}
return ans;
}
}
