离散数学(群、环、域)
代数系统
定义6.1.1:设 S 是一个非空集合,称 S×S 到 S 的一个映射 f 为 S 的一个二元代数运算,即,对于 S 中任意两个元素 a , b ,通过 f ,唯一确定 S 中一个元素 c : f(a,b)= c ,常记为 a * b = c 。
由于一般情况下, (a,b) , (b,a) 是 S×S 中不同的元,故 a * b 未必等于 b * a 。

-
二元代数运算应满足的两个条件
-
集合非空
-
封闭(运算结果属于集合)
-
定义6.1.2: 设 * 是集合 S 上的二元代数运算,如果对于 S 中任意两个元素 a , b ,等式 a * b = b * a 都成立,则称运算 “*” 满足交换律。
例如整数上的加法。
定义6.1.3: 设 * 是集合 S 上的二元代数运算,如果对于S中任意三个元素 a , b , c ,等式
(a * b) * c = a * (b * c)
都成立,则称运算 * 满足结合律。
例如整数上的加法。
定义6.1.4: 设 * 是集合 S 上的二元代数运算, a 是 S 中的元素,如果 a * a = a
则称 a 是关于运算 * 的幂等元。
如果 S 中每个元素都是关于 * 的幂等元,则称运算 “*” 满足等幂律。
如在整数中看,1是关于乘法的幂等元,0是关于加法的幂等元,但乘法和加法都不满足等幂律。
定义6.1.5: 设 * 和 + 是集合 S 上的两个二元代数运算,如果对于 S 中任意三个元素 a , b , c ,等式
a (b + c)= (a * b)+ (a * c) , (b + c) a =(b * a)+(c * a)
都成立,则称运算 * 对 + 满足分配律。
定义6.1.6: 设 * 和 + 是集合S上的两个二元代数运算,如果对于S中任意两个元素 a , b ,等式 a * (a + b) = a , a + (a * b) = a ,
都成立,则称运算 * 和 + 满足吸收律。
定义6.1.7: 设 * 是集合 S 上的二元代数运算,如果对于 S 中任意三个元素 a , b , c ,
(1)若 a * b = a * c ,则 b = c ,
(2)若 b * a = c * a ,则 b = c ,
就称 * 满足消去律。
定义6.1.8: 设 S 是一个非空集合, f1,……,fm 是 S 上的若干代数运算,把 S 及其运算 f1,……,fm 看成一个整体来看,叫做一个代数系统,
记为 (S, f1,……,fm)
零元 :设 * 是集合 S 上的二元代数运算,如果 S 中存在元素 θ ,使得对于S中任意元素 a,都有a * θ = θ , θ * a = θ ,则称 θ 是S上关于运算 * 的零元。
群的定义
半群
定义6.2.1: 设 G 是一个非空集合,若 · 为 G 上的二元代数运算,且满足结合律,则称该代数系统 (G, ·) 为半群。
-
半群的三个条件
-
集合非空
-
封闭(运算结果属于集合)
-
满足结合律
-
群
群的定义
定义6.2.2: 设(G, ·)为半群,如果满足下面条件:
(1)有壹(单位元): G中有一个元素1,适合对于G中任意元素a,都有1·a = a·1 = a;
(2) 有逆:对于G中任意a,都可找到G中一个元素 ,满足 ,则称(G, ·)为群。
如果群G包含的元素个数有限,则称G为有限群,否则称G为无限群。
理解群的定义
1️⃣ 单位元是群中唯一的幂等元。
2️⃣ 群中消去律一定成立。
3️⃣ 当|G|>1时,群中无零元。
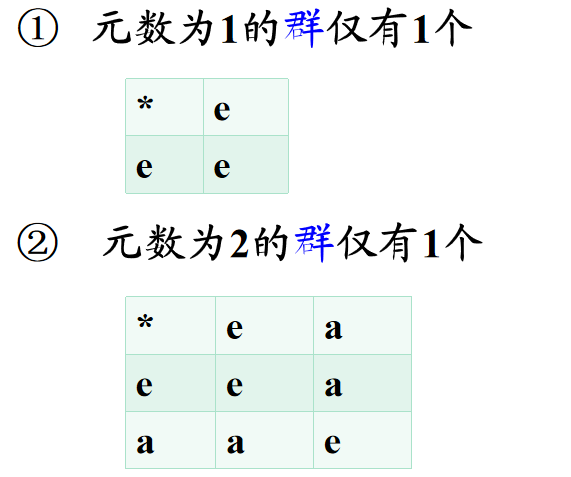
4️⃣ 群中消去律一定成立
5️⃣ 设(G,)是群,a, b∈G。如果ab=e,则b*a=e。
群的性质
1️⃣ 设(G, · )是一个群,则G中恰有一个元素1适合1·a=a·1=a, 而且对于任意a恰有一个元素
适合 。
也就是:群的单位元素是唯一的。任意元素的逆也是唯一的。
2️⃣ 群定义中的条件(1)和(2)可以减弱如下:
(1) G中有一个元素左壹适合1·a=a;
(2) 对于任意a,有一个元素左逆a-1适合 ·a=1。
注:把(1),(2) 中对于左边的要求一律改成对于右边的要求也是一样。 但是只满足左壹、右逆未必成群,只满足右壹、左逆也未必成群。
3️⃣ 群定义中的条件(1)和(2)等于下列可除条件:
对于任意a,b,有 x 使x · a=b,又有 y 使 a·y=b。
4️⃣ 若G是一个群,在一个乘积 a1…an 中可以任意加括号而求其值。
5️⃣ n个a连乘积为a的n次方,记为。我们规定
对于任意整数 m、n,
第一指数律
第二指数律 。
但一般群中第三指数定律不成立,因为不一定满足交换律
6️⃣ 消去律成立
7️⃣ 其运算表中每一行或每一列中元素互不相同
8️⃣ 存在唯一的幂等元 1(单位元)
9️⃣ 一元群、二元群、三元群是唯一的,且都是 交换群。
1️⃣0️⃣ 有限半群,满足消去条件,一定是群.
Abel 群
Abel 群的定义
定义6.2.3: 若群(G, · )的运算·适合交换律,则称(G, · )为 Abel群 或 交换群 。
Abel 群的性质
1️⃣ 在一个Abel群(G,·)中,一个乘积可以任意颠倒因子的次序而求其值。
2️⃣ 在Abel群中,有第三指数律:,m为任意整数。
3️⃣ 加法群: (G,+) 永远假定加法群是一个Abel群
置换群
置换的定义
1️⃣ 集合 A 到 A 上的映射称为 变换。
2️⃣ 设 M 是一个非空的有限集合,M的一个一 对一变换称为一个置换。
3️⃣ M 的置换共有 n!个。M 上的置换也称为 n元置换。特别地, 若 σ(ai)=ai,i=1,2,…,n,则 σ 为 n元恒等置换。
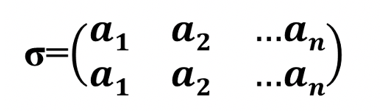
4️⃣ Sn 就是 n!个置换作成的集合。(就是 Sn 中元素全排列的所有组成方式构成一个集合)

置换的乘法
对M中任意元素a及M的任意两个置换σ、τ,στ(a)=σ(τ(a))。
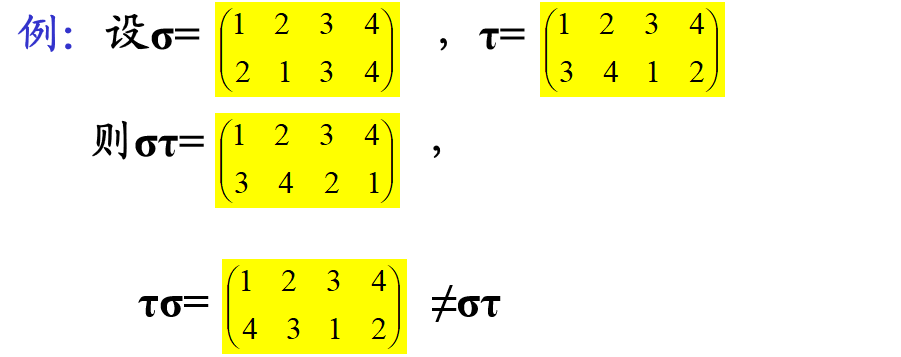
置换的乘法的性质
1️⃣ 满足结合律:(στ)ρ=σ(τρ),σ,τ,ρ∈ Sn
2️⃣ Sn中有单位元:n元恒等置换,设为 ,有: τ=τ ,τ∈Sn
3️⃣ 每个n元置换在Sn 中都有逆元素:
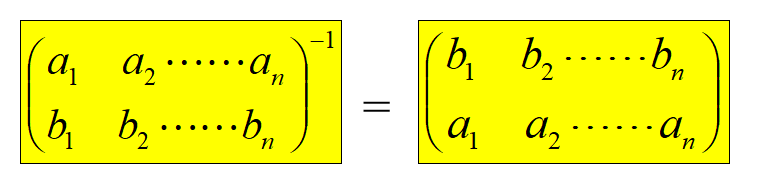

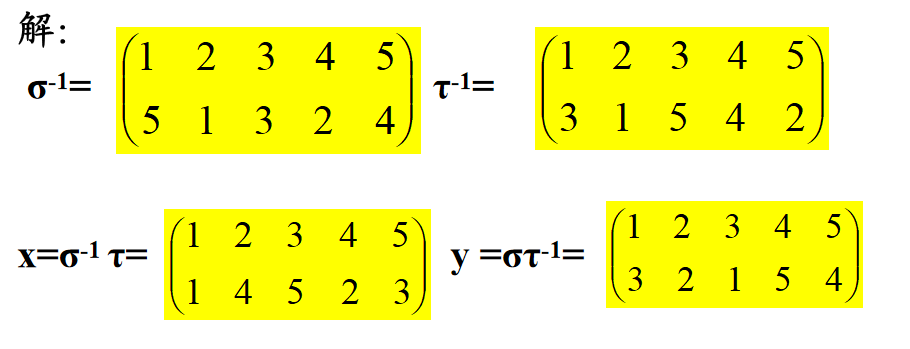
n 次对称群
n 元置换的全体作成的集合 Sn 对置换的乘法作成一个群,称为 n 次对称群。(n 次对称群的任一子群称为 n 次置换群)
🔔 由于一般情况下置换相乘不满足交换律,τσ στ ,当 n≥3 时,Sn 不是交换群。


置换的轮换表法
设 σ 是 M 的置换,若可取到 M 的元素 a1, … , ar,使 σ(a1)=a2, σ(a2)=a3, … , σ(ar-1)=ar, σ(ar)=a1,而 σ 不变换 M 的其余的元素,则 σ 称为一个轮换,记为:(a1 a2 … ar)。
🔔 可以把a1, … , ar中的任意元素ai排在头一位而改写成:(ai ai+1 … ar a1 … ai-1)
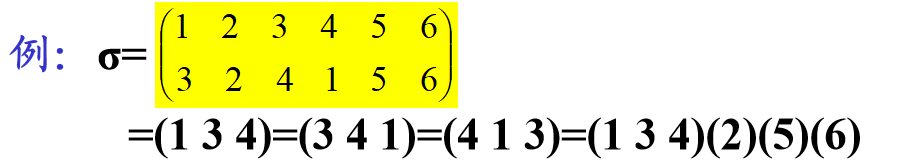
📪 设 是M的轮换,则
不相杂轮换
M 的两个轮换 σ=( a1 … ar)和τ=( b1 … bs)说是不相杂或不相交,如果 a1, …, ar和b1, …, bs都不相同。(即 )

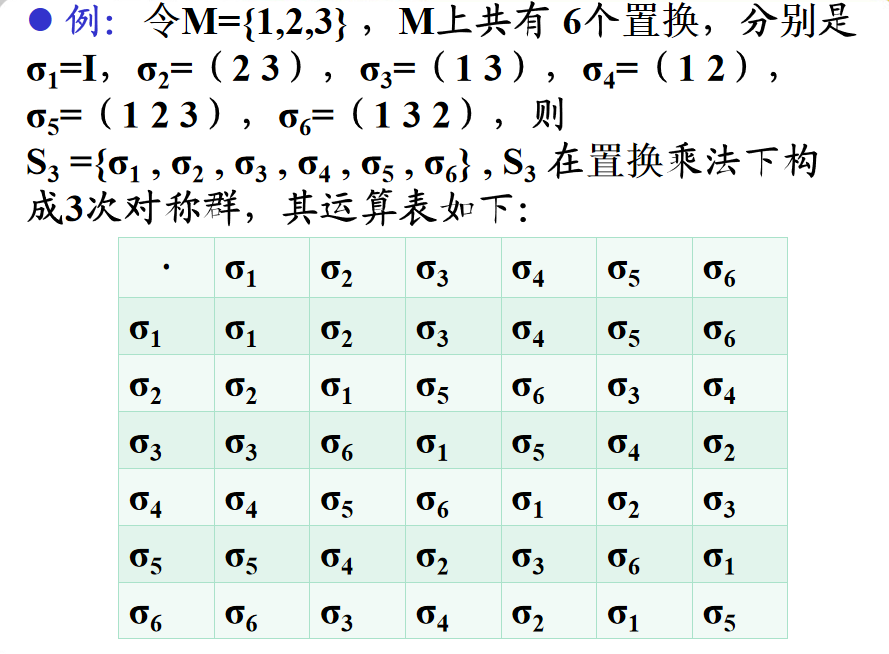
1️⃣ 若σ和τ是M的两个不相杂的轮换,则其乘法适合交换律:στ=τσ。
2️⃣ 任意置换σ恰有一法写成不相杂轮换的乘积。即,任意置换σ可以写成不相杂轮换的乘积(可表性),如果不考虑乘积的顺序,则写法是唯一的(唯一性)。

3️⃣ 任意置换σ恰有一法写成不相杂的轮换乘积。

对换
设(a1a2…ar)为一轮换,我们称r为该 轮换的长度---轮换的长度也就是其中所含的元素个数.
对换:长度为2的轮换称为 对换。
1️⃣ 任意轮换可以写成对换的乘积。(每个小对换中第一个元素固定,其他元素按轮换逆序匹配)
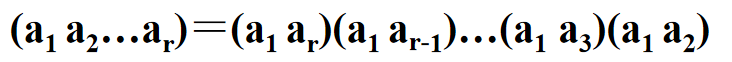
2️⃣ 对任意 n 元置换 (n>1),有一法(但未必只有一法)可将其写成一些对换的乘积。这里,乘积中出现的诸对换已非不相杂。而且,表示方法也不唯一。如(1 2)=(1 2)(1 3)(1 3)=(2 3)(1 3)(2 3)
置换的奇偶性
-
第一种判别法:置换总元素数 n - 轮换个数 k 。即 n - k 为奇数(偶数),则称σ为奇置换(偶置换)

-
第二种判别法:置换表示成对换之后,所有对换的个数 n 为奇数(偶数),则称σ为奇置换(偶置换)

1️⃣ 每个置换都能分解为对换的乘积, 但偶置换只能分解为偶数个对换的乘积, 奇置换只能分解为奇数个对换的乘积。

2️⃣ 设 M 的元数为 n, 若 n>1 ,则奇置换的个数和偶置换的个数相等,因而都等于 n!/2

子群及其陪集
子群的定义
设(G,·)是一个群, H G, 如果按照G中的乘法运算· ,(H, ·) 仍是一个群,则(H,·)叫做(G,·)的子群。如果G的一个子群H不等于G,即H G则(H,·)叫做 (G,·)的真子群。
🔔 G的子群H的运算必须与G的运算一样,比如, (C*,·)不是(C,+)的子群。

平凡子群和非平凡子群
任意一个群G都有两个明显的子群,称为 G 的平凡子群:
- 由其单位元素组成的子群{1},称为 G 的单位子群;
- G 本身。
其余的子群(如果有的话)称为非平凡子群。
子群的判别条件
判别条件一
群 G 的一个子集 H 是 G 的一个子群的充分必要条件是:
- 若a∈H,b ∈ H,则a·b ∈ H;
- 若a ∈ H,则a-1 ∈ H;
- H非空。
判别条件二
- 若a∈H, b∈H,则a·b-1∈H。
- H非空。
判别条件三
- 群 G 的一个有限非空子集 H 是 G 的一个子群的充分必要条件是 H 对 G 的运算是封闭的,即若 a ∈H,b∈H,则 ab ∈ H。
子群与大群的关系
子群 H 与大群 G 的关系:
- H 的单位元就是 G 的单位元,
- H 中任一元素 a 在 H 中的逆元也就是 a 在 G 中的逆元。
循环群
设 a 是群 G 的一个元素。于是 a 的所有幂的集合 做成 G 的一个子群,记为 (a)。此群称为由 a 生成的子群。
如果 G 可以由它的某元素 a 生成,即有 a ∈G 使 G =(a),群 G 叫做一个循环群,或巡回群。于是子群(a)可称为由 a 生成的循环子群。
🔔 每个循环群是 Abel 群。
元素的周期

1️⃣ 群中单位元的周期为1,(1)={1}。
2️⃣ 群中任一元素和它的逆元具有同样的周期.
3️⃣ 若群 G 中元素 a 的周期为 n,则
4️⃣ 设 a 为群 G 的一个元素
- 如果 a 的周期为无穷大,则 (a) 是无限循环群,(a) 由彼此不同的元素
组成。 - 如果 a 的周期为 n,则(a)为 n 元循环群它由 n 个不同的元素
组成。
加法群中元素的周期
在加法群中,(a)应换为a的所有倍数的集合 …,-2a,-a,0,a,2a,… () 当()中的所有元素均彼此不同时,称 a 的周期为无穷大或为 0;否则当 n 为适合 na=0 的最小正整数时,称 a 的周期为 n.

若加法群中 a 的周期为 n,则有
- 0,a,2a,…,(n-1)a 为 n 个不同元素
- ma=0 当且仅当 n∣m
- sa=ta 当且仅当 n∣(s-t).
循环群的生成元素
1️⃣ 无限循环群(a)一共有两个生成元:a及a-1.
2️⃣ n 元循环群(a)中,元素 ak 是(a)的生成元的充要条件是(n,k)=1。
所以(a)一共有φ(n)个生成元素。

🔔 模 m 加法群是循环群

🔔 循环群的子群仍然是循环群

陪集
设 G 是群,H 是 G 的子群,a,b∈G,若有 h∈H,使得 a = bh,则称 a 合同于 b(右模 H),记为 a≡b(右mod H)。
🔔 合同关系(右模H)是一个等价关系。
右陪集:群G在合同关系(右模H)下的一个等价类叫做 H 的一个右陪集
左陪集:同样,可以定义a合同于b(左模H):a≡b(左modH)和 H 的左陪集。
🌈 求陪集的简单方法


1️⃣ 设 H 是群 G 的有限子群,则 H 的任意右陪集 aH 的元数皆等于 H 的元数 即 |aH| = |H|。
2️⃣ H本身也是H的右陪集。
3️⃣ aH=H iff a∈H 🔔 常用
4️⃣ a 在陪集 aH 中
5️⃣ 对于右陪集 aH 中任意元素 b,都有 aH=bH。说明右陪集aH中任一元素都可以做陪集代表
6️⃣ aH=bH 的充分必要条件是 。
7️⃣ 任意两个右陪集 aH 和 bH 或者相等或者不相交。
正规子群
设 H 是群 G 的子群,设对 G 中的任意元素 g,都有 gH=Hg,则称 H 是 G 的正规子群。
1️⃣ “平凡”子群 H={1} 和 G 都是 G 的正规子群.
2️⃣ Abel 群的任意子群是正规子群
3️⃣ H 是 G 的正规子群,必要而且只要对任意的
4️⃣ 设 H 是 G 的子群,证明如果 H 的任意两个右陪集的乘积仍是一个右陪集,则 H 是 G 的正规子群。


拉格朗日定理
设 G 为有限群,则 G 的任意子群 H 的元数整除群 G 的元数。
🔔 拉格朗日定理的逆命题不成立:设 G 是有限群,且|G|=n,对任意 n 的正因数 m ,G 不一定存在元数个数为 m 的子群。
1️⃣ 若 G 为有限群,并且|G|=n,则 G 的任意子群的元数均为 n 的因子;反过来,对于 n 的任意一个因子 m,G 未必有 m 元子群。
2️⃣ 若 G 是循环群,且|G|=n ,则对于 n 的任意一个正因数 m,G 一定存在且仅存在一个 m 元子群
3️⃣ 元数是质数的群,一定没有非平凡子群。
4️⃣ 设 G 是有限群,且|G|=n , 则 G 中任意元素的周期一定为 n 的因子。
5️⃣ 设 G 是元数为质数 p 的循环群,则对于 G 中任意不是单位元的元素 a,a 都是生成元(由一、四结论得到。任意子群的元数均为 n 的因子(n),G 中任意元素的周期一定为 n 的因子(n)).
H 在 G 中的指数:有限群 G 的元数除以 H 的元数所得的商,记为(G:H),称作 H 在 G 中的指数。(等价类的个数)
🔔 H 的指数也就是 H 的右(左)陪集的个数
右代表系:从每个右陪集中选出一个元素为代表全体代表的集合叫做一个右代表系或右代表团。
1️⃣ 设G为有限群,元数为n,对任意a∈G,有 。
2️⃣ 设有限交换群(G,·)中所有元素之积不等于单位元1,G必为偶数元群。
3️⃣ 若群 G 的元数是一个质数,则 G 必是循环群。

🔔 当n<6时,n元群均是交换群(Abel 群)。
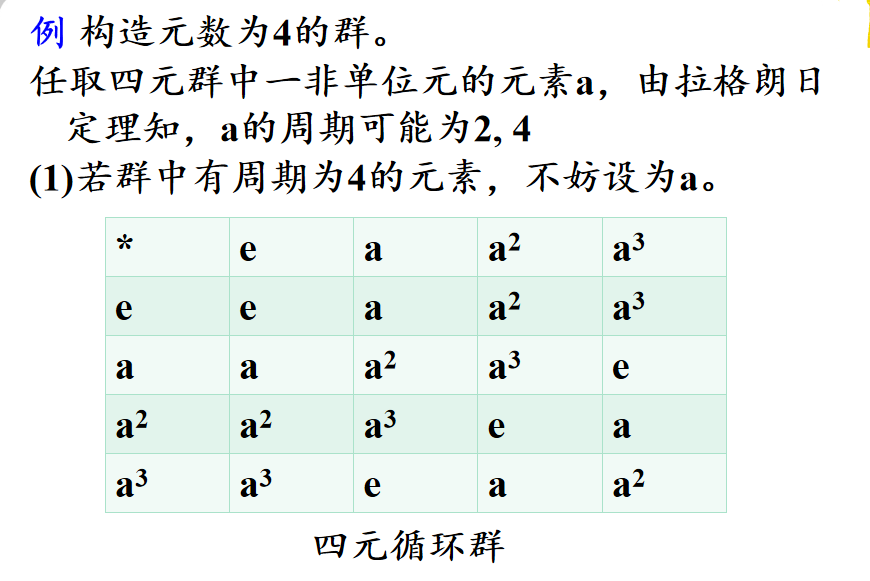
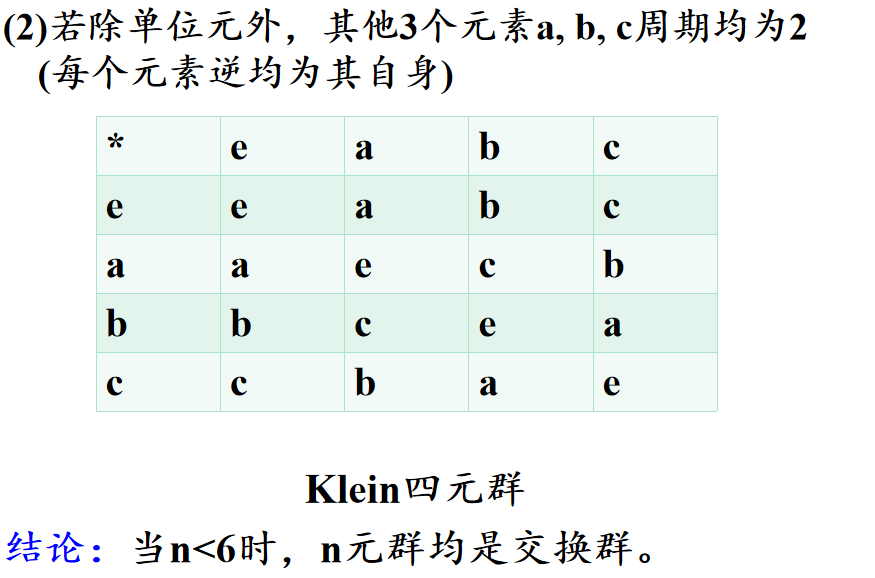
🔔 4元群只有两种可能:4元循环群或Klein四元群。

群的同态及同构
同态映射
定义: 设(G, *)是一个群, (K, •)是一个代数系统,称G到K的一个映射σ是一个同态映射,如果对G中任意元素a,b ,有
σ(a * b)=σ(a) • σ(b)
🔔 注意:这个映射既不一定是单射也不一定是满射。
🌋 解释:一、 A的所有元素必须都有映像;但B中不要求每个元素都有原像;二、可以A中的多个元素对应b中的一个元素;但不允许A中的一个元素对应b中的多个元素;
设(G, *)是一个群, (K, •)是一个代数系统, σ是G到K中的一个同态映射, G’=σ(G) ,则
1️⃣ (G’ , •)是一个群;
2️⃣ G’的单位元1’就是G的单位元1的映像σ(1) ,即1’= σ(1);
3️⃣ 对任意
4️⃣ 若σ(a)= σ(b),则
同构映射
定义: 设G是一个群,K是一个代数系统,σ是G到K内的一个同态映射,如果σ是G到σ(G)上的1-1映射,则称σ是同构映射。称G与σ(G)同构,记成G ≌ σ(G)。
🌰
1️⃣ 整数加法群(Z,+)同构于偶数加法群(B,+)
2️⃣ 无限循环群同构于整数加法群。
3️⃣ (R*,·)与(R,+)不可能同构。
自同构映射
定义:设G是一个群,若σ是G到G上的同构映射,则称σ为自同构映射。
同态核
定义: 设σ是G到G′上的一个同态映射,命N为G中所有映射到G′中1′的元素g的集合,记为σ-1(1′),即
则称 N 为 σ 的核。
🔔 同态核是正规子群
群的第一同态定理
定理:设σ是群G到Gˊ上的一个同态映射,于是,σ的核N是G的一个正规子群, 对于Gˊ的任意元素aˊ,
是N在G中的一个陪集,因此,Gˊ的元素和N在G中的陪集一一对应。
🔔 设N是群G的正规子群。若A,B是N的陪集,则AB也是N的陪集。
群的第二同态定理
定理: 设N是群G的正规子群,于是按照陪集的乘法,N的所有陪集作成一个群。
命 σ:a→aN,a ∈G,
则σ是G到 上的一个同态映射,且σ的核就是N。
称为G对于N的商群,记为G ∕ N。
若G是有限群,则商群中元素个数等于N在G中的指数,即等于陪集的个数。
群的第三同态定理
定理: 设σ是群G到G′上的一个同态映射,若σ的核为N,则G′≌ G/N。
G中子群与G’中子群的关系
设σ为群G到G′上的同态映射。
1️⃣ 若H为G之子群,则 H′=σ(H)亦为G′之子群。
2️⃣ 若H′为G′之子群,则 亦必为G之子群,其中
3️⃣ 
4️⃣
5️⃣ 若 N H ,则HN=H, 即
6️⃣ H是G的正规子群必要而且只要 H’=σ(H)是G’的正规子群。
7️⃣ G与N之间的子群和G′的子群一一对应,大群对应大群,小群对应小群,正规子群对应正规子群。
🌋 注意:G与N之间的子群指的是比N大比G小的子群。所以有N⊆H。G与N之间的子群,没说G的子群,G的子群,跟G’的子群之间不是一一映射
环
🌋 两张图概括
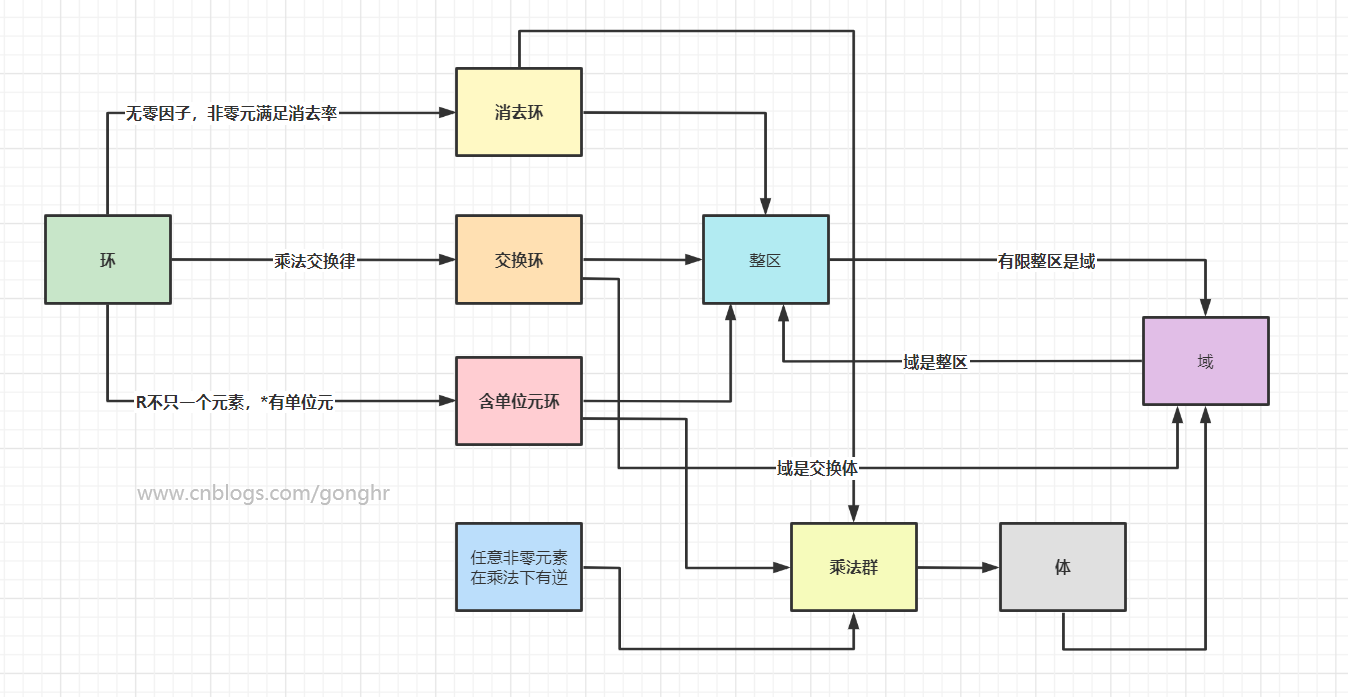
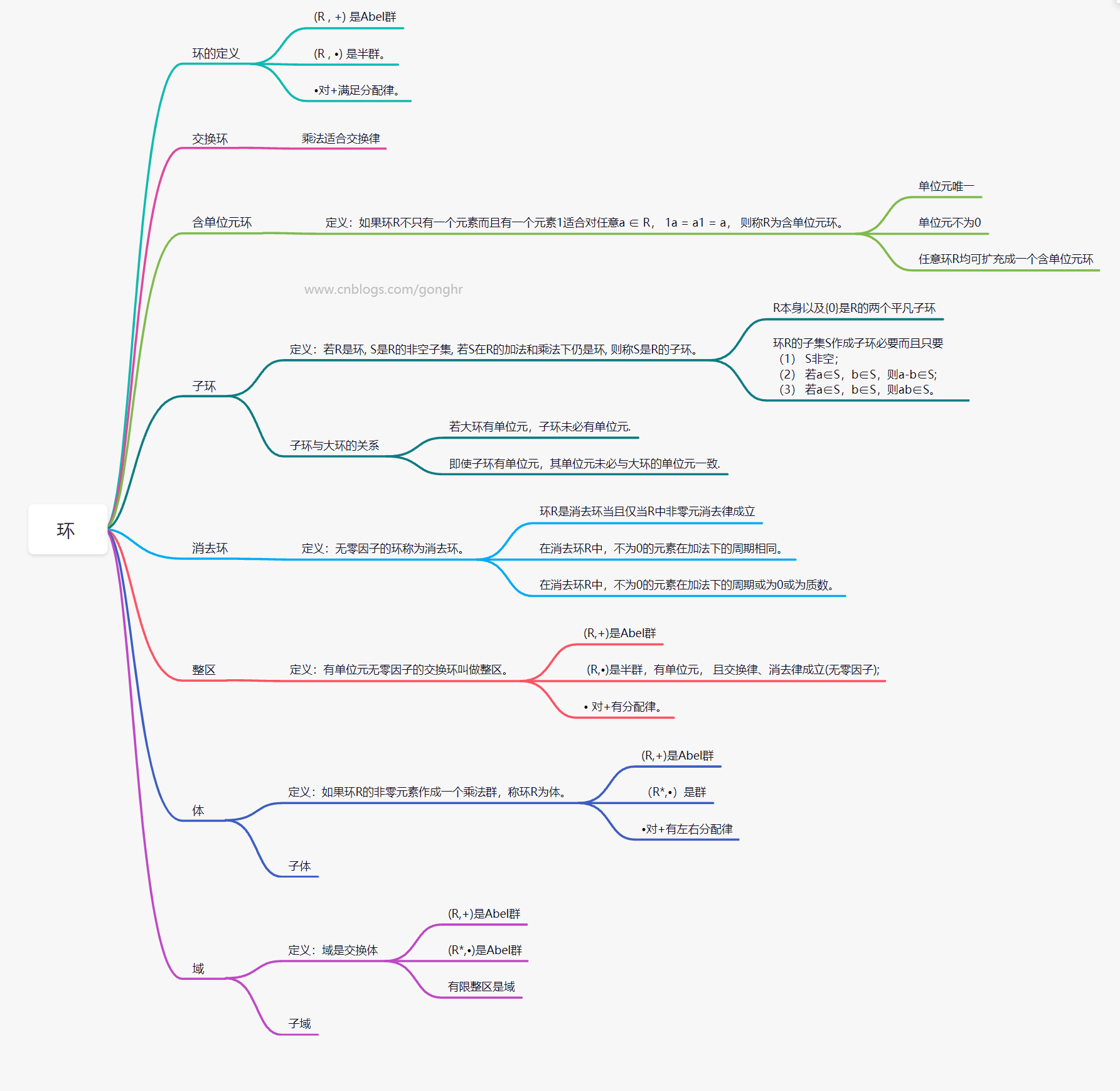
往期回顾
离散数学(集合论)
离散数学(古典数理逻辑)
离散数学(图与网络)
离散数学(数论基础)
离散数学(格与布尔代数)
离散数学(群、环、域)
本文作者:GHR
本文链接:https://www.cnblogs.com/gonghr/p/15234188.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。


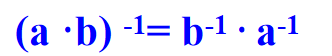
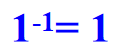



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步