【数据结构与算法】前缀和与差分
前缀和
一维前缀和
前缀和数组 sum 的每一位记录的是当前位置距离起点位置,这连续一段的和区间和。
利用前缀和数组,我们可以快速得到数组任意区间的元素和。
构造前缀和数组的时间复杂度是O(n),获得区间和的复杂度是O(1)

当nums数组的元素下标从0开始算时,需要做出一些调整

模板和例题
给定一个整数数组 nums,求出数组从索引 i 到 j(i ≤ j)范围内元素的总和,包含 i、j 两点。
实现 NumArray 类:
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 从索引 i 到 j(i ≤ j)范围内元素的总和,包含 i、j 两点(也就是 sum(nums[i], nums[i + 1], ... , nums[j]))
示例:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]
解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
提示:
0 <= nums.length <= 104
-105 <= nums[i] <= 105
0 <= i <= j < nums.length
最多调用 104 次 sumRange 方法
class NumArray {
int[] sum;
public NumArray(int[] nums) {
int n = nums.length;
// 前缀和数组下标从 1 开始,因此设定长度为 n + 1(模板部分)
sum = new int[n + 1];
// 预处理除前缀和数组(模板部分)
for (int i = 1; i <= n; i++)
sum[i] = sum[i - 1] + nums[i - 1];
}
public int sumRange(int i, int j) {
// 求某一段区域和 [i, j] 的模板是 sum[j] - sum[i - 1](模板部分)
// 但由于我们原数组下标从 0 开始,因此要在模板的基础上进行 + 1
i++; j++;
return sum[j] - sum[i - 1];
}
}
二维前缀和
用来解决二维矩阵中的矩形区域求和问题
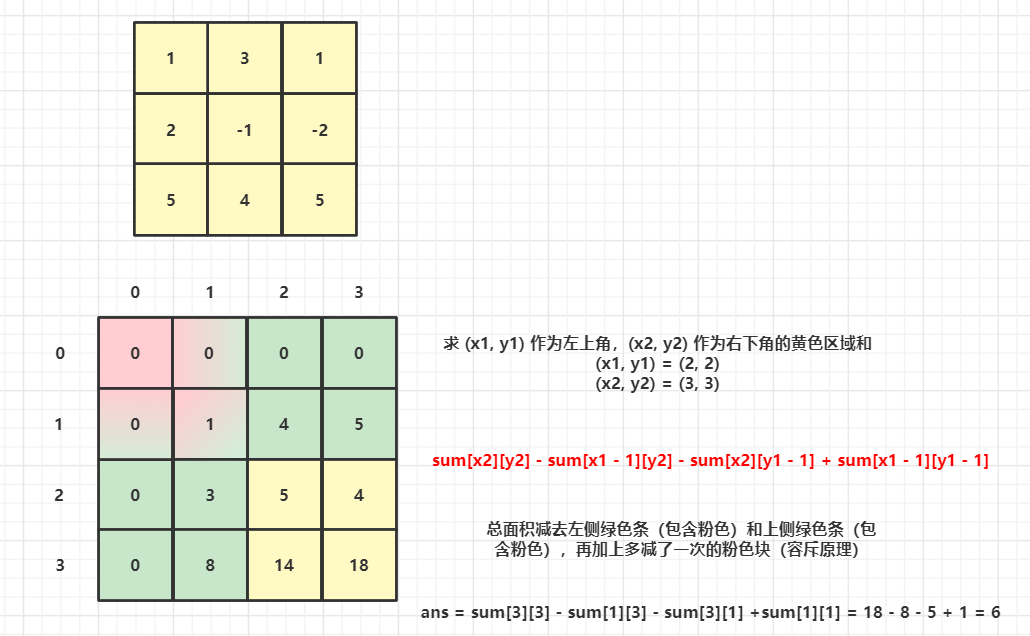
sum矩阵中每一个数(x, y)表示(0, 0)为左上角到(x, y)为右下角的矩形数值总和
模板和例题
// 预处理前缀和数组
{
sum = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 当前格子(和) = 上方的格子(和) + 左边的格子(和) - 左上角的格子(和) + 当前格子(值)【和是指对应的前缀和,值是指原数组中的值】
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
// 首先我们要令左上角为 (x1, y1) 右下角为 (x2, y2)
// 计算 (x1, y1, x2, y2) 的结果
{
// 前缀和是从 1 开始,原数组是从 0 开始,上来先将原数组坐标全部 +1,转换为前缀和坐标
x1++; y1++; x2++; y2++;
// 记作 22 - 12 - 21 + 11,然后 不减,减第一位,减第二位,减两位
// 也可以记作 22 - 12(x - 1) - 21(y - 1) + 11(x y 都 - 1)
ans = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}

给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。
示例 1:
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 104 次 sumRegion 方法
class NumMatrix {
int[][] sum;
public NumMatrix(int[][] matrix) {
int n = matrix.length, m = n == 0 ? 0 : matrix[0].length;
// 与「一维前缀和」一样,前缀和数组下标从 1 开始,因此设定矩阵形状为 [n + 1][m + 1](模板部分)
sum = new int[n + 1][m + 1];
// 预处理除前缀和数组(模板部分)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
public int sumRegion(int x1, int y1, int x2, int y2) {
// 求某一段区域和 [i, j] 的模板是 sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];(模板部分)
// 但由于我们源数组下标从 0 开始,因此要在模板的基础上进行 + 1
x1++; y1++; x2++; y2++;
return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}
}
差分
一维差分
「差分」是求「前缀和」的逆向过程。
但是差分数组的构造过程并不重要,利用差分的性质实现区间修改和单点查询是重点
差分数组的求法:c[i] = nums[i] - nums[i-1],原数组中相邻元素的差值组成的数组就是差分数组
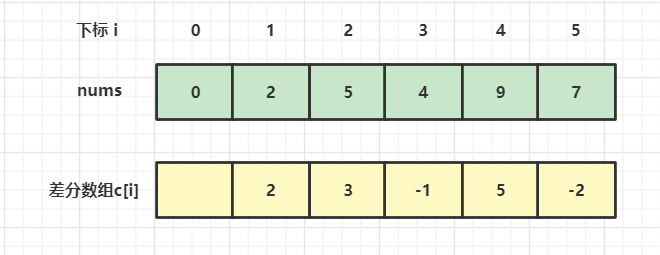
差分数组对应的概念是前缀和数组,差分数组的第 i 个数即为原数组的第 i-1 个元素和第 i 个元素的差值,也就是说我们对差分数组求前缀和即可得到原数组。
差分数组的性质是,当我们希望对原数组的某一个区间 [l,r] 施加一个增量inc 时,差分数组 d 对应的改变是:d[l] 增加 inc,d[r+1] 减少 inc。这样对于区间的修改就变为了对于两个位置的修改。并且这种修改是可以叠加的,即当我们多次对原数组的不同区间施加不同的增量,我们只要按规则修改差分数组即可。
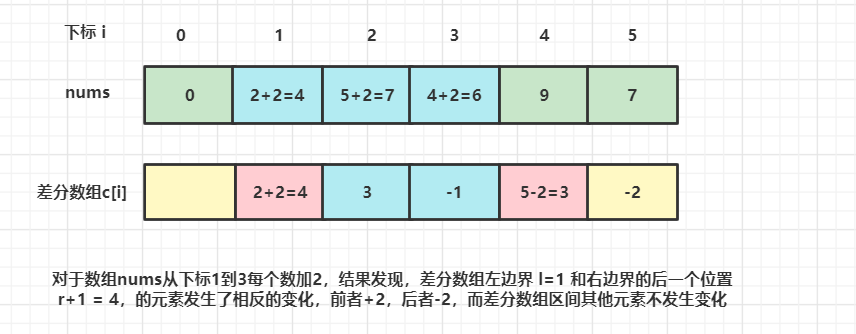
当对一个区间进行增减某个值的时候,他的差分数组对应的区间左端点的值会同步变化,而他的右端点的后一个值则会相反地变化
模板和例题
这里有 n 个航班,它们分别从 1 到 n 进行编号。
有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座位。
请你返回一个长度为 n 的数组 answer,其中 answer[i] 是航班 i 上预订的座位总数。
示例 1:
输入:bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出:[10,55,45,25,25]
解释:
航班编号 1 2 3 4 5
预订记录 1 : 10 10
预订记录 2 : 20 20
预订记录 3 : 25 25 25 25
总座位数: 10 55 45 25 25
因此,answer = [10,55,45,25,25]
示例 2:
输入:bookings = [[1,2,10],[2,2,15]], n = 2
输出:[10,25]
解释:
航班编号 1 2
预订记录 1 : 10 10
预订记录 2 : 15
总座位数: 10 25
因此,answer = [10,25]
提示:
1 <= n <= 2 * 104
1 <= bookings.length <= 2 * 104
bookings[i].length == 3
1 <= firsti <= lasti <= n
1 <= seatsi <= 104
class Solution {
public int[] corpFlightBookings(int[][] bs, int n) {
int[] c = new int[n + 1];
for (int[] bo : bs) {
int l = bo[0] - 1, r = bo[1] - 1, v = bo[2];
c[l] += v;
c[r + 1] -= v;
}
int[] ans = new int[n];
ans[0] = c[0];
for (int i = 1; i < n; i++) {
ans[i] = ans[i - 1] + c[i];
}
return ans;
}
}
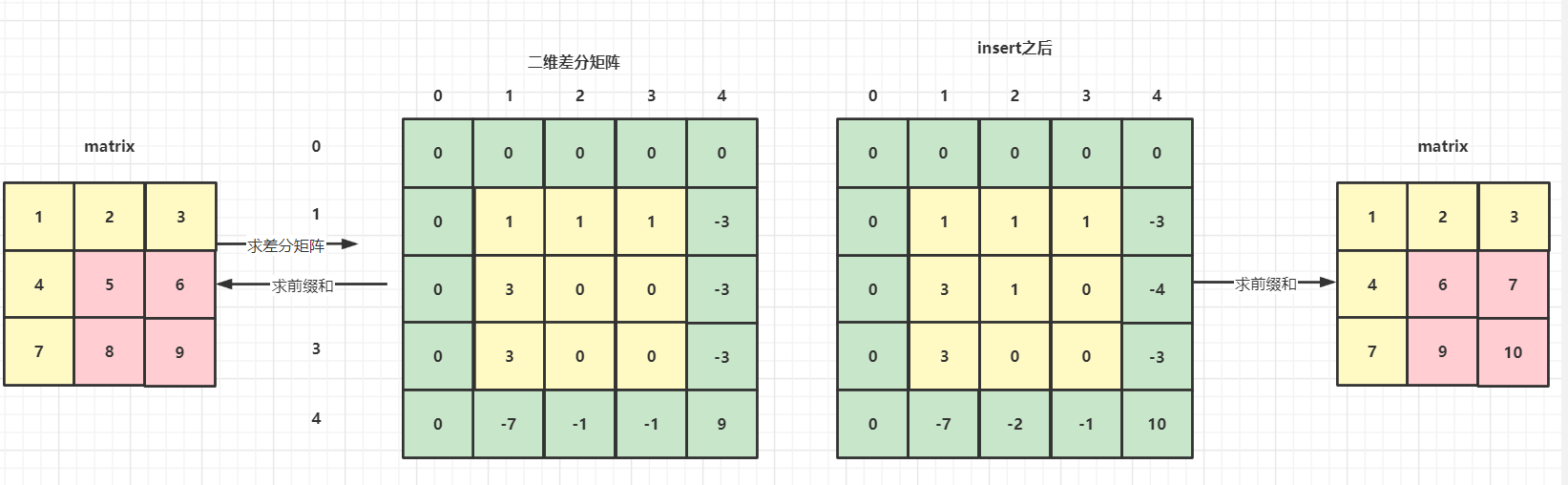
二维差分
differ[x1][y1] += c; //原矩阵(x1,y1)到右下角的值都加c
differ[x2 + 1][y1] -= c; //原矩阵(x2+1,y1)到右下角的值都加c
differ[x1][y2 + 1] -= c; //原矩阵(x1,y2+1)到右下角的值都加c
differ[x2 + 1][y2 + 1] += c; //原矩阵(x2+1,y2+1)到右下角多减去了c,再加回来
模板和例题
给定一个二维矩阵 matrix,以下请求:
令子矩形范围内每个元素的加或减一个常数c,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
依次输入二维矩阵, (row1, col1) ,(row2, col2) ,c
并返回处理后的二维矩阵
示例1:
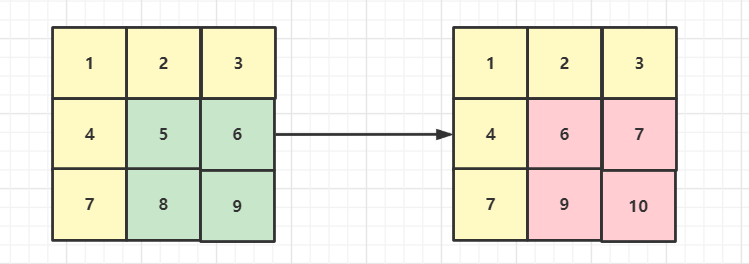
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]],1,1,2,2,1
输出:[[1,2,3],[4,6,7],[7,9,10]]
public class demo1 {
static int[][] differ; //二维差分数组
static int m, n;
public static void main(String[] args) {
int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
int[][] ans = diff(matrix, 1, 1, 2, 2, 1);
System.out.println(Arrays.deepToString(ans));
}
public static void insert(int x1, int y1, int x2, int y2, int c) { //差分数组的构造
differ[x1][y1] += c;
differ[x2 + 1][y1] -= c;
differ[x1][y2 + 1] -= c;
differ[x2 + 1][y2 + 1] += c;
}
public static int[][] diff(int[][] matrix, int x1, int y1, int x2, int y2, int c) {
m = matrix.length;
n = m == 0 ? 0 : matrix[0].length;
differ = new int[m + 2][n + 2];
//所给matrix下标都从0开始,而差分数组的下标必须从1,开始,所以下标做一定的调整
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
insert(i + 1, j + 1, i + 1, j + 1, matrix[i][j]);
}
}
insert(x1 + 1, y1 + 1, x2 + 1, y2 + 1, c); //二维差分矩阵
//求二维前缀和
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
differ[i][j] = differ[i - 1][j] + differ[i][j - 1] - differ[i - 1][j - 1] + differ[i][j];
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
matrix[i - 1][j - 1] = differ[i][j];
}
}
return matrix;
}
}
//输出:[[1, 2, 3], [4, 6, 7], [7, 9, 10]]

