【数据结构与算法】二叉树模板及例题
二叉树节点结构
class Node<V>{
V value;
Node left;
Node right;
}
二叉树的遍历(递归)
先序遍历
顺序:根左右
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
中序遍历
顺序:左根右
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
后序遍历
顺序:左右根
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
二叉树的遍历(非递归)
先序遍历
顺序:根左右
先把根节点压入栈中,每次
-
从栈中弹出一个节点cur
-
处理节点cur
-
先压入cur的右节点,再压入cur的左节点(如果有的话)
只要栈不为空,周而复始
public static void preOrder(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null)
stack.push(head.right);
if (head.left != null)
stack.push(head.left);
}
System.out.println();
}
中序遍历
顺序:左根右
-
每棵子树整棵树左边界进栈
-
依次弹出的过程中处理节点
-
对弹出节点右树做同样操作
周而复始
public static void inOrder(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<>();
while (!stack.isEmpty() || head != null) { //刚开始stack为空,head不为null
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
System.out.println();
}
}
后序遍历
顺序:左右根
反过来就是根右左,准备两个栈。
先把根节点压入栈1中,每次
-
从栈1中弹出一个节点cur
-
把节点cur压入栈2
-
先在栈1中压入cur的右节点,再压入cur的左节点(如果有的话)
只要栈1不为空,周而复始
最后依次弹出栈2中的节点,其顺序就是后序遍历的顺序
public static void postOrder(Node head) {
if (head != null) {
Stack<Node> stack1 = new Stack<>();
Stack<Node> stack2 = new Stack<>();
stack1.push(head);
while (!stack1.isEmpty()){
head = stack1.pop();
stack2.push(head);
if(head.left!=null){
stack1.push(head.left);
}
if(head.right!=null){
stack1.push(head.right);
}
}
while (!stack2.isEmpty()){
head = stack2.pop();
System.out.print(head.value+" ");
}
System.out.println();
}
}
二叉树层序(宽度)遍历
先把根节点放入队列中,每次
-
弹出节点cur
-
处理节点cur
-
先把cur的左节点放入队列,再把cur的右节点放入队列(如果存在的话)
周而复始,直到队列为空
public static void leverOrder(Node head) {
if (head != null) {
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
System.out.print(head.value + " ");
if (head.left != null) {
queue.add(head.left);
}
if (head.right != null) {
queue.add(head.right);
}
}
System.out.println();
}
}
public static void leverOrder(Node head) {
if (head == null) return;
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while (!queue.isEmpty()) {
int n = queue.size();
for (int i = 0; i < n; i++) { //一次处理一层节点
head = queue.poll();
System.out.printf(head.value + " ");
if (head.left != null) queue.add(head.left);
if (head.right != null) queue.add(head.right);
}
}
System.out.println();
}
二叉树应用题
二叉树深度
递归
class Solution {
public int maxDepth(TreeNode root) {
if(root==null) return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
}
层序遍历bfs
public int maxDepth(TreeNode root) {
if(root==null) return 0;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
int ans = 0;
while(!queue.isEmpty()){
ans++; //每次处理一层,处理完ans加一
int n = queue.size();
for(int i = 0;i < n; i++){
root = queue.poll();
if(root.left!=null) queue.add(root.left);
if(root.right!=null) queue.add(root.right);
}
}
return ans;
}
求二叉树最大宽度
层序遍历的过程中使用HashMap记录节点层数
public static void maxWidth(Node head) {
if (head != null) {
Queue<Node> queue = new LinkedList<>();
queue.add(head);
HashMap<Node, Integer> levelMap = new HashMap<>();
levelMap.put(head, 1);
int curLevel = 1; //当前层数
int curLevelNodes = 0; //当前层数的节点数
int max = Integer.MIN_VALUE;
while (!queue.isEmpty()) {
Node cur = queue.poll();
int curNodeLevel = levelMap.get(cur); //获取当前节点层数
if (curNodeLevel == curLevel) { //当前节点层数等于当前层数,节点数加一
curLevelNodes++;
} else {
max = Math.max(max, curLevelNodes); //否则max取较大值
curLevel++; //当前层数加一
curLevelNodes = 1; //重置当前层数的节点数为1
}
if (cur.left != null) {
levelMap.put(cur.left, curNodeLevel + 1);
queue.add(cur.left);
}
if (cur.right != null) {
levelMap.put(cur.right, curNodeLevel + 1);
queue.add(cur.right);
}
}
System.out.println(max);
}
}
判断是否为搜索二叉树
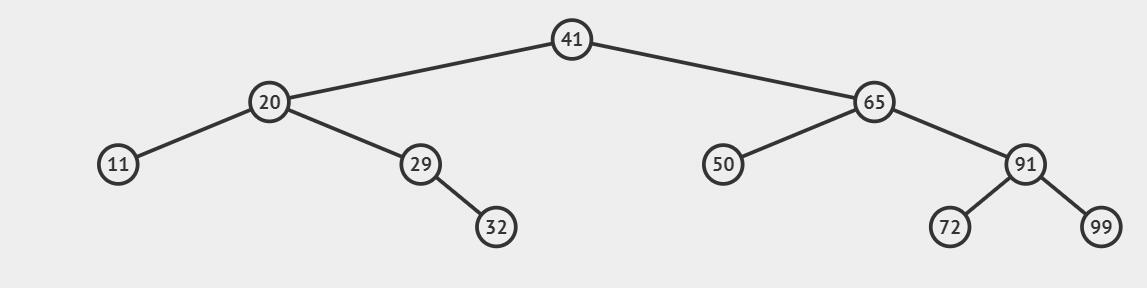
中序遍历递增就是搜索二叉树
递归方式
public static int preValue = Integer.MIN_VALUE;
public static boolean checkBST(Node head){
if(head!=null){
boolean isLeftBst = checkBST(head.left);
if(!isLeftBst){
return false;
}
if(head.value<=preValue){
return false;
}else{
preValue = head.value;
}
return checkBST(head.right);
}
return true;
}
非递归方式
public static boolean checkBST(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<>();
while (!stack.isEmpty() || head != null) { //刚开始stack为空,head不为null
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
if(head.value<=preValue){
return false;
}else {
preValue = head.value;
}
head = head.right;
}
}
}
return true;
}
树形DP处理
-
左子树是搜索二叉树
-
右子树是搜索二叉树
-
根节点大于左子树最大值
-
根节点小于右子树最小值
public static boolean isBST(Node head){
return process(head).isBST;
}
public static class ReturnType {
public boolean isBST;
public int max;
public int min;
public ReturnType(boolean isBST, int max, int min) {
this.isBST = isBST;
this.max = max;
this.min = min;
}
}
public static ReturnType process(Node x){
if(x==null) {
return null;
}
ReturnType leftData = process(x.left); //获取左子树处理信息
ReturnType rightData = process(x.right); //获取右子树处理信息
int min = x.value;
int max = x.value;
if(leftData!=null){ //获取当前树的最大值最小值
min = Math.min(min,leftData.min);
max = Math.max(max,leftData.max);
}
if(rightData!=null){
min = Math.min(min,rightData.min);
max = Math.max(max,rightData.max);
}
boolean isBST = true;
//左子树存在并且(左子树不是BST或者左子树最大值大于x)
if(leftData!=null&&(!leftData.isBST||leftData.max>=x.value)){
isBST = false;
}
//右子树存在并且(右子树不是BST或者右子树最小值小于x)
if(rightData!=null&&(!rightData.isBST||x.value>=rightData.min)){
isBST = false;
}
return new ReturnType(isBST,max,min);
}
判断是否是完全二叉树
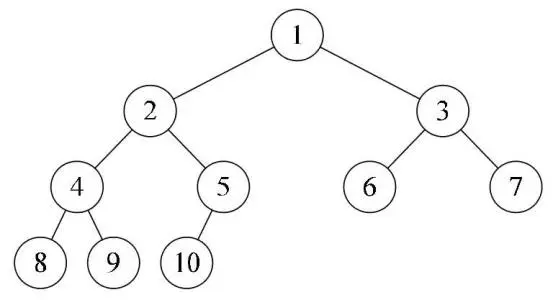
-
层序遍历
-
任何一个节点有右孩子没左孩子,则不是完全二叉树(1)
-
在(1)的前提下,遇到第一个左右不双全节点,那其后面必须都是叶子节点,否则不是二叉树
public static boolean checkCBT(Node head) {
if (head != null) {
boolean leaf = false; //是否遇到过左右不双全节点
Node l = null;
Node r = null;
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
if ((leaf && !(l == null && r == null)) //遇到第一个左右不双全节点,那么以后的节点都必须是叶子节点
||
(l == null && r != null)) { //任何一个节点有右孩子没左孩子
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
}
if (l == null || r == null) {
leaf = true;
}
}
}
return true;
}
判断是否是平衡二叉树
-
左子树是平衡的
-
右子树是平衡的
-
左右子树高度差的绝对值小于2
获取左树信息和右树信息后,结合处理。属于树形DP
public static boolean isBalancd(Node head) {
return process(head).isBalanced;
}
public static class ReturnType { //封装了平衡状态和高度
public boolean isBalanced;
public int height;
public ReturnType(boolean isB, int hei) {
isBalanced = isB;
height = hei;
}
}
public static ReturnType process(Node x) {
if (x == null) { //空树是平衡的,高度为0
return new ReturnType(true, 0);
}
ReturnType leftData = process(x.left); //左树
ReturnType rightData = process(x.right); //右树
int height = Math.max(leftData.height, rightData.height) + 1; //获取左子树和右子树的最高高度+1
boolean isBalanced = leftData.isBalanced && rightData.isBalanced && //如果左子树平衡,右子树平衡
Math.abs(leftData.height - rightData.height) < 2; //左右子树的高度差的绝对值小于2
return new ReturnType(isBalanced, height); //返回新状态
}
判断是否是满二叉树
如果一个二叉树的层数为K,且结点总数是 (2^k) -1 ,则它就是满二叉树。
树形DP问题
public static boolean isFull(Node head) {
if (head == null) {
return true;
}
Info data = process(head);
return data.nodes == ((1 << data.height) - 1);//是否层数为K,且结点总数是 (2^k) -1
}
public static class Info { //封装树的高度和节点数
public int height;
public int nodes;
public Info(int h, int n) {
height = h;
nodes = n;
}
}
public static Info process(Node x) {
if (x == null) {
return new Info(0, 0);
}
Info leftData = process(x.left); //获取左子树信息
Info rightData = process(x.right); //获取右子树信息
int height = Math.max(leftData.height, rightData.height) + 1; //求新高度
int nodes = leftData.nodes + rightData.nodes + 1; //求总的节点数
return new Info(height, nodes);
}
在二叉树中找到一个节点的后继节点
现在有一种新的二叉树节点类型如下:
public class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int val) {
value = val;
}
}
该结构比普通二叉树节点结构多了一个指向父节点的parent指针。
假设有一棵Node类型的节点组成的二叉树,树中每个节点的parent指针都正确地指向自己的父节点,头节 点的parent指向null。 只给一个在二叉树中的某个节点node,请实现返回node的后继节点的函数。
在二叉树的中序遍历的序列中, node的下一个节点叫作node的后继节点。
-
一个节点有右子树,那么它的下一个节点就是它的右子树中的最左子节点。例如b的后继节点是h。
-
一个节点没有右子树时分两种情况:
- 当前节点是它父节点的左子节点,那么它的下一个节点就是它的父节点。 例如节点f的后继节点是c,节点d的后继节点是b。
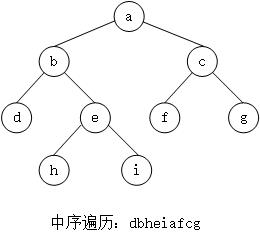
- 当前节点是它父节点的右子节点,此时沿着指向父节点的指针一直向上遍历,直到找到一个是它父节点的左子节点的节点,如果这个节点存在,那么这个节点的父节点就是我们要找的下一个节点。如下图所示: f的下一个节点是a。
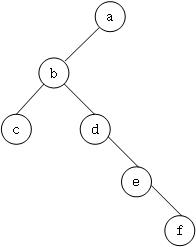
- 当前节点是它父节点的左子节点,那么它的下一个节点就是它的父节点。 例如节点f的后继节点是c,节点d的后继节点是b。
public static class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int data) {
this.value = data;
}
}
public static Node getSuccessorNode(Node node) {
if (node == null) {
return node;
}
if (node.right != null) {
return getLeftMost(node.right);
} else {
Node parent = node.parent;
while (parent != null && parent.left != node) {
node = parent;
parent = node.parent;
}
return parent;
}
}
public static Node getLeftMost(Node node) {
if (node == null) {
return node;
}
while (node.left != null) {
node = node.left;
}
return node;
}
折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后 展开。 此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。 如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从 上到下依次是下折痕、下折痕和上折痕。 给定一个输入参数N,代表纸条都从下边向上方连续对折N次。 请从上到下打印所有折痕的方向。
例如:
N=1时,打印: down
N=2时,打印: down down up
分析:
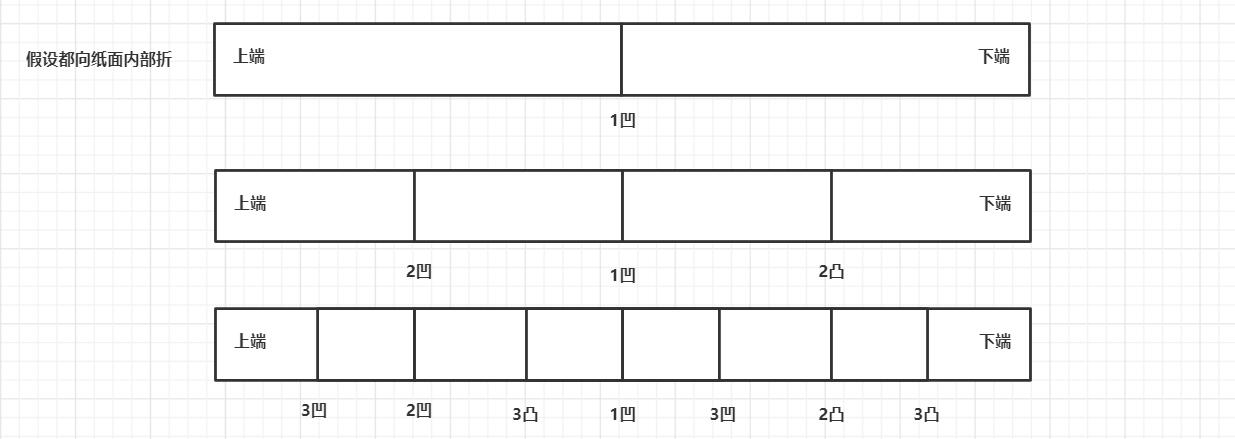
发现第n+1次的折痕中凹折痕一定在第n次折痕的左边,第n+1次折痕中凸折痕一定在第n次折痕的右边
形成一棵二叉树
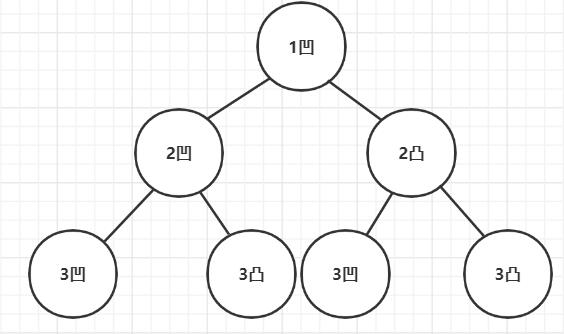
中序遍历该二叉树就可得到答案
public static void printAllFolds(int N) {
printProcess(1, N, true);
}
public static void printProcess(int i, int N, boolean down) {
if (i > N) {
return;
}
printProcess(i + 1, N, true);
System.out.println(down ? "down " : "up ");
printProcess(i + 1, N, false);
}
public static void main(String[] args) {
int N = 1;
printAllFolds(N);
}
对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
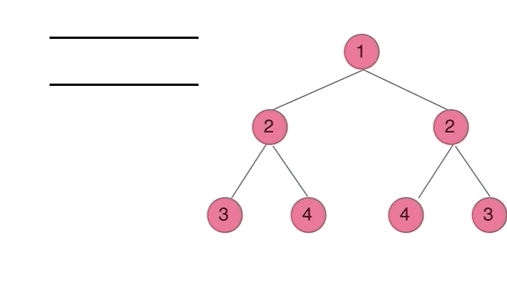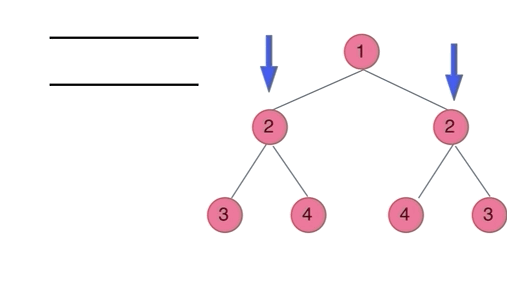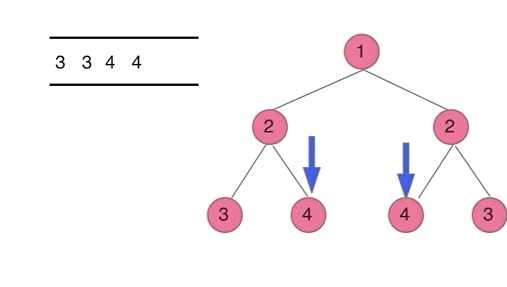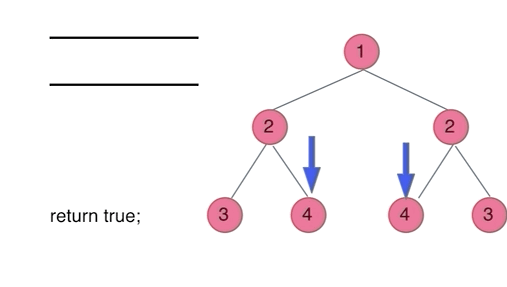
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
进阶:
你可以运用递归和迭代两种方法解决这个问题吗?
法一:递归
-
当前节点是祖宗根节点:比较左右子树
-
当前是左子树根节点和右子树根节点:比较左子树的左子树和右子树的右子树、左子树的右子树和右子树的左子树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
return judge(root.left, root.right);
}
public boolean judge(TreeNode left, TreeNode right) {
if (left == null && right != null) return false;
if (left != null && right == null) return false;
if (left == null && right == null) return true;
if (left.val != right.val) return false;
return judge(left.left, right.right) && judge(left.right, right.left);
}
}
法二:BFS
用一个队列模拟层序遍历,每次放入和弹出两个元素
class Solution {
public boolean isSymmetric(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root.left);
queue.add(root.right);
while (!queue.isEmpty()) {
TreeNode left = queue.poll();
TreeNode right = queue.poll();
if (left == null && right == null) continue; //true放在最后返回
if (left == null || right == null || left.val != right.val) return false;
queue.add(left.left); //注意顺序
queue.add(right.right);
queue.add(left.right);
queue.add(right.left);
}
return true;
}
}
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104
法一:递归
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q != null) return false;
if (p != null && q == null) return false;
if (p == null && q == null) return true;
if (p.val != q.val) return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
法二:BFS
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(p);
queue.add(q);
while (!queue.isEmpty()) {
TreeNode left = queue.poll();
TreeNode right = queue.poll();
if (left == null && right == null) continue;
if (left == null || right == null || left.val != right.val) return false;
queue.add(left.left);
queue.add(right.left);
queue.add(left.right);
queue.add(right.right);
}
return true;
}
}
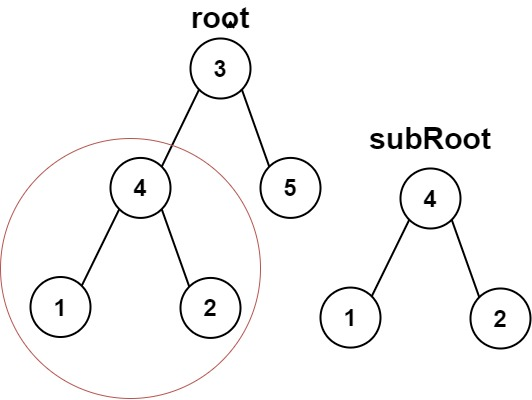
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104
法一:递归
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
if (t == null) return true; // t 为 null 一定都是 true
if (s == null) return false; // 这里 t 一定不为 null, 只要 s 为 null,肯定是 false
return isSubtree(s.left, t) || isSubtree(s.right, t) || isSameTree(s,t);
}
/**
* 判断两棵树是否相同
*/
public boolean isSameTree(TreeNode s, TreeNode t){
if (s == null && t == null) return true;
if (s == null || t == null) return false;
if (s.val != t.val) return false;
return isSameTree(s.left, t.left) && isSameTree(s.right, t.right);
}
}
二叉树最小深度
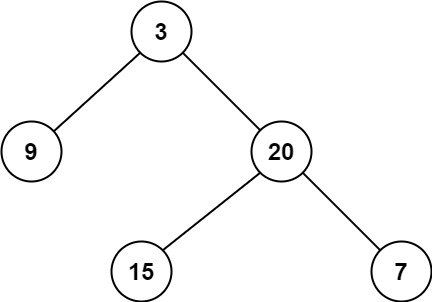
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
法一:后序遍历
class Solution {
/**
* 递归法,相比求MaxDepth要复杂点
* 因为最小深度是从根节点到最近**叶子节点**的最短路径上的节点数量
*/
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftDepth = minDepth(root.left);
int rightDepth = minDepth(root.right);
if (root.left == null) {
return rightDepth + 1;
}
if (root.right == null) {
return leftDepth + 1;
}
// 左右结点都不为null
return Math.min(leftDepth, rightDepth) + 1;
}
}
法二:层序遍历
每一次层数加一,如果某节点左右子树为空,则说明找到最小深度,返回result
class Solution {
/**
* 迭代法,层序遍历
*/
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
int depth = 0;
while (!deque.isEmpty()) {
int size = deque.size();
depth++;
for (int i = 0; i < size; i++) {
TreeNode poll = deque.poll();
if (poll.left == null && poll.right == null) {
// 是叶子结点,直接返回depth,因为从上往下遍历,所以该值就是最小值
return depth;
}
if (poll.left != null) {
deque.offer(poll.left);
}
if (poll.right != null) {
deque.offer(poll.right);
}
}
}
return depth;
}
}
完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
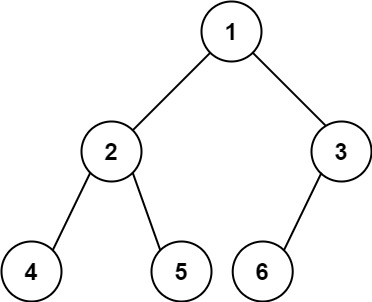
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树
法一:递归
class Solution {
// 通用递归解法
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
法二:二叉树性质
class Solution {
/**
* 针对完全二叉树的解法
*
* 满二叉树的结点数为:2^depth - 1
*/
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
}
int leftDepth = getDepth(root.left);
int rightDepth = getDepth(root.right);
if (leftDepth == rightDepth) {// 左子树是满二叉树
// 2^leftDepth其实是 (2^leftDepth - 1) + 1 ,左子树 + 根结点
return (1 << leftDepth) + countNodes(root.right);
} else {// 右子树是满二叉树
return (1 << rightDepth) + countNodes(root.left);
}
}
private int getDepth(TreeNode root) {
int depth = 0;
while (root != null) {
root = root.left;
depth++;
}
return depth;
}
}
二叉树的序列化和反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
提示: 输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
示例 1:
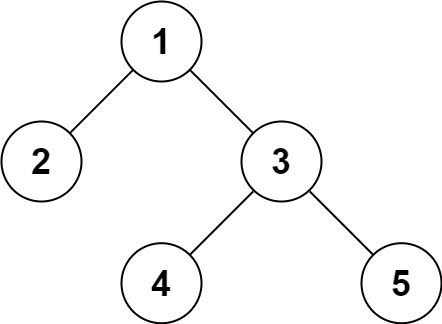
输入:root = [1,2,3,null,null,4,5]
输出:[1,2,3,null,null,4,5]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[1,2]
提示:
树中结点数在范围 [0, 104] 内
-1000 <= Node.val <= 1000
法一:中序遍历
public class Codec {
int INF = -2000;
TreeNode emptyNode = new TreeNode(INF);
public String serialize(TreeNode root) {
if (root == null) return "";
StringBuilder sb = new StringBuilder();
Deque<TreeNode> d = new ArrayDeque<>();
d.addLast(root);
while (!d.isEmpty()) {
TreeNode poll = d.pollFirst();
sb.append(poll.val + "_");
if (!poll.equals(emptyNode)) {
d.addLast(poll.left != null ? poll.left : emptyNode);
d.addLast(poll.right != null ? poll.right : emptyNode);
}
}
return sb.toString();
}
public TreeNode deserialize(String data) {
if (data.equals("")) return null;
String[] ss = data.split("_");
int n = ss.length;
TreeNode root = new TreeNode(Integer.parseInt(ss[0]));
Deque<TreeNode> d = new ArrayDeque<>();
d.addLast(root);
for (int i = 1; i < n - 1; i += 2) {
TreeNode poll = d.pollFirst();
int a = Integer.parseInt(ss[i]), b = Integer.parseInt(ss[i + 1]);
if (a != INF) {
poll.left = new TreeNode(a);
d.addLast(poll.left);
}
if (b != INF) {
poll.right = new TreeNode(b);
d.addLast(poll.right);
}
}
return root;
}
}
二叉搜索树节点最小距离
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
示例 1:
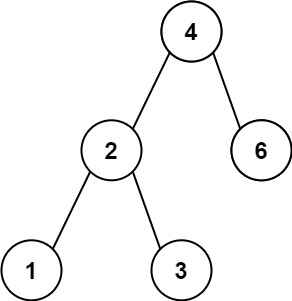
输入:root = [4,2,6,1,3]
输出:1
示例 2:
输入:root = [1,0,48,null,null,12,49]
输出:1
提示:
树中节点数目在范围 [2, 100] 内
0 <= Node.val <= 105
差值是一个正数,其数值等于两值之差的绝对值
中序遍历的过程中不断更新距离最小值
class Solution {
int ans = Integer.MAX_VALUE;
TreeNode prev = null;
public int minDiffInBST(TreeNode root) {
Deque<TreeNode> d = new ArrayDeque<>();
while (root != null || !d.isEmpty()) {
while (root != null) {
d.addLast(root);
root = root.left;
}
root = d.pollLast();
if (prev != null) {
ans = Math.min(ans, Math.abs(prev.val - root.val));
}
prev = root;
root = root.right;
}
return ans;
}
}
二叉树中所有距离为 K 的结点
给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 K 。
返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。
示例 1:
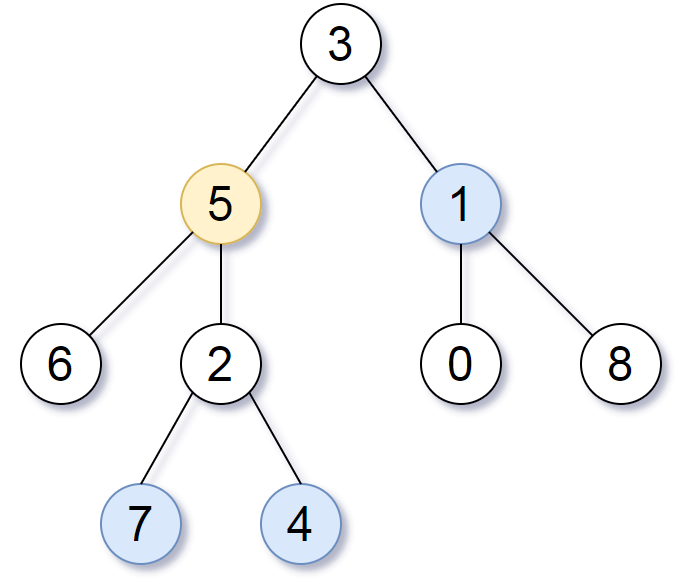
输入:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出:[7,4,1]
解释:
所求结点为与目标结点(值为 5)距离为 2 的结点,
值分别为 7,4,以及 1
注意,输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。
提示:
给定的树是非空的。
树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
目标结点 target 是树上的结点。
0 <= K <= 1000.
法一:建图+BFS
二叉树一个节点最多有两条边连接到左孩子和右孩子,属于稀疏图,可以利用邻接表存储。
之后从target开始进行k次BFS即可,这里可以理解成扩散,每次扩散用vis数组记录,以target为中心扩散k次以后就获得了所有距离target为k的节点
这里邻接表用到的结构是链式前向星。本质就是数组模拟链表,并且采用头插法。
int[] he = new int[N], e = new int[M], ne = new int[M];
int idx;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
- idx 是用来对边进行编号
- he 数组:存储是某个节点所对应的边的集合(链表)的头结点;
- e 数组:由于访问某一条边指向的节点;
- ne 数组:由于是以链表的形式进行存边,该数组就是用于找到下一条边,存储下一条边的索引;
class Solution {
// 根据数据范围最多有 501 个点,每个点最多有 2 条无向边(两个子节点)
int N = 510, M = N * 4;
int[] he = new int[N], e = new int[M], ne = new int[M];
int idx;
void add(int a, int b) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx++;
}
boolean[] vis = new boolean[N];
public List<Integer> distanceK(TreeNode root, TreeNode t, int k) {
List<Integer> ans = new ArrayList<>();
Arrays.fill(he, -1);
dfs(root);
Deque<Integer> d = new ArrayDeque<>();
d.addLast(t.val);
vis[t.val] = true;
while (!d.isEmpty() && k >= 0) {
int size = d.size();
while (size-- > 0) {
int poll = d.pollFirst();
if (k == 0) {
ans.add(poll);
continue;
}
for (int i = he[poll]; i != -1 ; i = ne[i]) {
int j = e[i];
if (!vis[j]) {
d.addLast(j);
vis[j] = true;
}
}
}
k--;
}
return ans;
}
void dfs(TreeNode root) {
if (root == null) return;
if (root.left != null) {
add(root.val, root.left.val);
add(root.left.val, root.val);
dfs(root.left);
}
if (root.right != null) {
add(root.val, root.right.val);
add(root.right.val, root.val);
dfs(root.right);
}
}
}
二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/ \
2 3
\
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
使用前序遍历,当遇到叶子节点时进行结果处理,否则不断添加节点值进行dfs,遇到叶子节点后进行回溯,每次移除list的最后一个元素。
class Solution {
List<String> ans = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
List<Integer> list = new ArrayList<>();
dfs(root,list);
return ans;
}
public void dfs(TreeNode root,List<Integer> s){
if(root == null){
return;
}
s.add(root.val);
if(root.left==null && root.right==null){
StringBuilder sb = new StringBuilder("");
for(int i = 0;i<s.size();i++){
sb.append(s.get(i));
if(i!=s.size()-1)
sb.append("->");
}
ans.add(sb.toString());
return ;
}
if(root.left!=null){
dfs(root.left,s);
s.remove(s.size()-1); //回溯
}
if(root.right!=null){
dfs(root.right,s);
s.remove(s.size()-1); //回溯
}
}
}
左叶子之和
计算给定二叉树的所有左叶子之和。
示例:
3
/ \
9 20
/ \
15 7
在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
法一:递归
必须从父节点才能判断为左叶子
class Solution {
int ans = 0;
public int sumOfLeftLeaves(TreeNode root) {
if(root == null) return 0;
int leftValue = sumOfLeftLeaves(root.left);
int rightValue = sumOfLeftLeaves(root.right);
int midValue = 0;
if(root.left!=null && root.left.left == null && root.left.right == null){
midValue = root.left.val;
}
return midValue + leftValue + rightValue;
}
}
法二:层序遍历BFS
class Solution {
int ans = 0;
public int sumOfLeftLeaves(TreeNode root) {
level(root);
return ans;
}
public void level(TreeNode root) {
if (root != null) {
Deque<TreeNode> q = new ArrayDeque<>();
q.addLast(root);
while (!q.isEmpty()) {
TreeNode node = q.pollFirst();
if (node.left != null) {
q.addLast(node.left);
if (node.left.left == null && node.left.right == null)
ans += node.left.val;
}
if (node.right != null) {
q.addLast(node.right);
}
}
}
}
}
路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
示例 3:
输入:root = [1,2], targetSum = 0
输出:false
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
法一:递归
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root == null) return false;
targetSum -= root.val;
if(root.left == null && root.right == null){
return targetSum == 0;
}
if(root.left != null){
boolean left = hasPathSum(root.left, targetSum);
if(left != false) return true;
}
if(root.right != null){
boolean right = hasPathSum(root.right, targetSum);
if(right != false) return true;
}
return false;
}
}


